Uncertainty Quantification Module

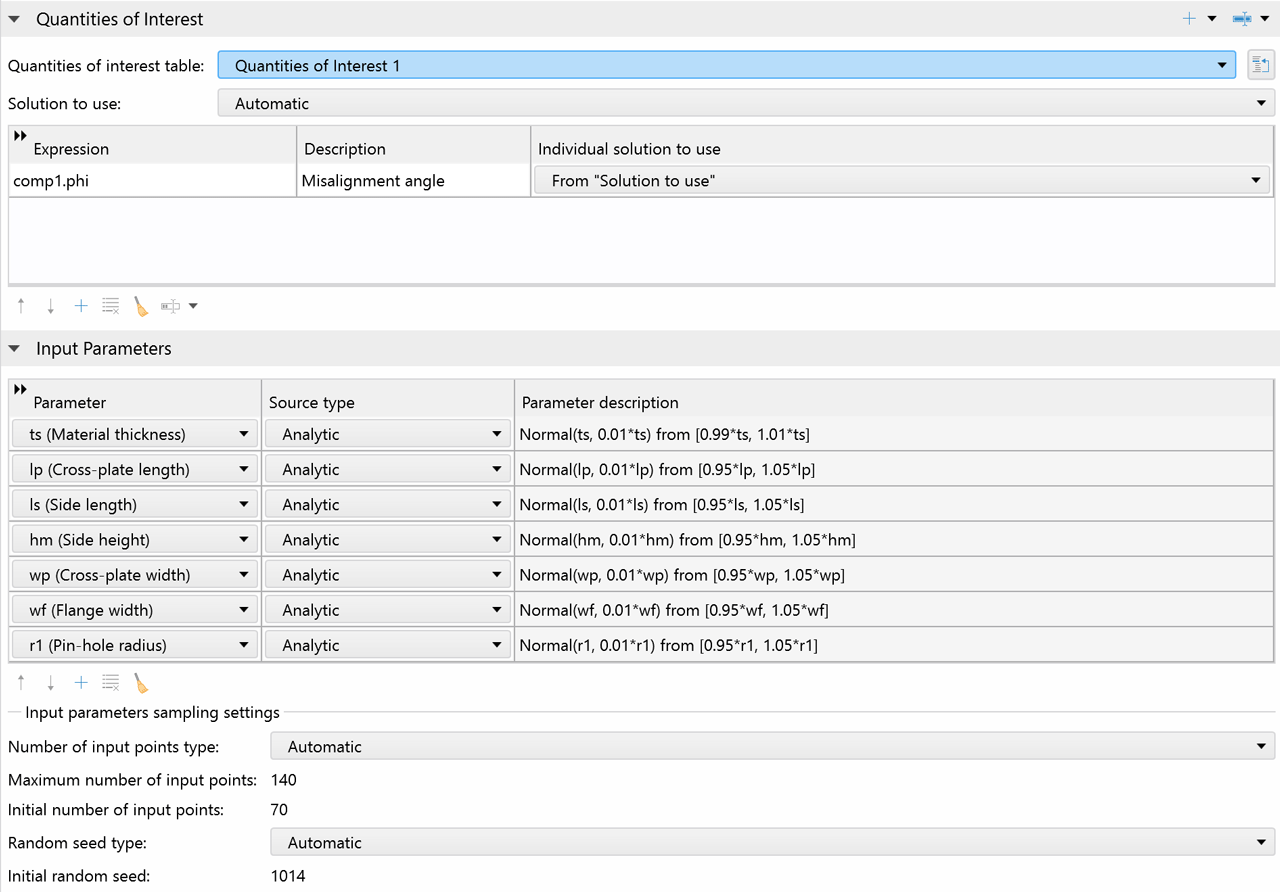
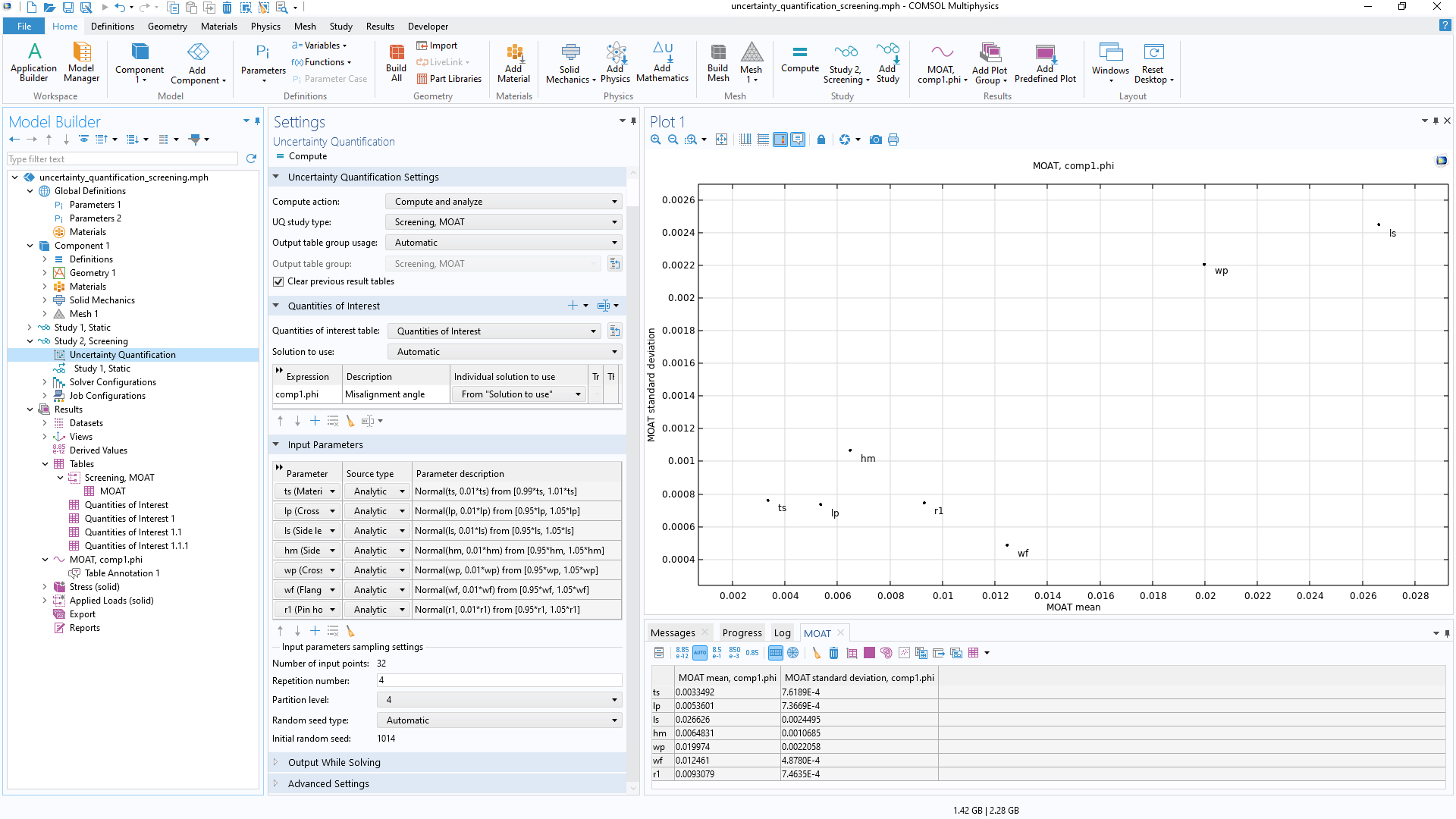
Eingabeparameter und Größen von Interesse

Wenn Sie eine Studie zur Unsicherheitsquantifizierung durchführen, definieren Sie eine Reihe von interessierenden Größen in Bezug auf eine COMSOL Multiphysics^® Modelllösung. Auf diese Weise sind die Größen von Interesse Funktionen der Eingabeparameter.

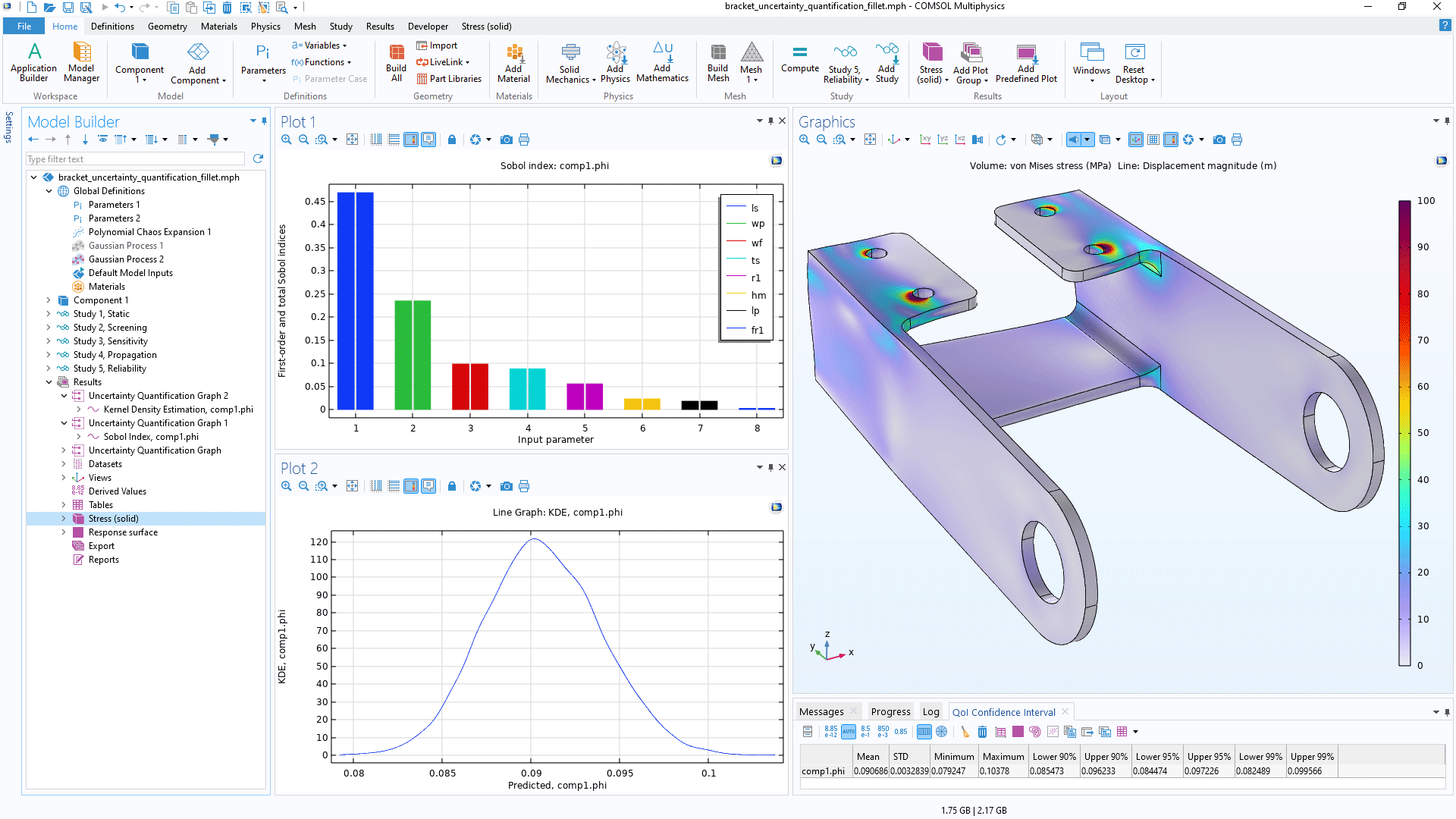
Im Falle einer Strukturanalyse können die interessierenden Größen die maximale Verschiebung, die Spannung oder der Beugewinkel sein. Bei einer Wärmetransport- oder CFD-Analyse können die interessierenden Größen die maximale Temperatur, der Gesamtwärmeverlust oder die gesamte Strömungsrate sein. Bei einer elektromagnetischen Simulation kann es sich um Widerstand, Kapazität oder Induktivität handeln. Da das Uncertainty Quantification Module auf jedes mit der Software COMSOL Multiphysics^® berechnete physikalische Modell sowie auf jeden mathematischen Ausdruck verschiedener gelöster Feldgrößen anwendbar ist, sind die Auswahlmöglichkeiten für die interessierenden Größen endlos.

Die analytisch gesampelten Eingabeparameter können korreliert und unkorreliert sein, wobei korrelierte Eingabeparameter in Korrelationsgruppen gruppiert und mit der Gauß-Copula-Methode gesampelt werden können. Jede unsichere Modelleingabe, sei es eine physikalische Einstellung, eine geometrische Dimension, eine Materialeigenschaft oder eine Diskretisierungseinstellung, kann als Eingabeparameter behandelt werden, und jede Modellausgabe kann zur Definition der interessierenden Größen verwendet werden.

Sensitivitätsanalyse

Der Studientyp Sensitivity Analysis wird verwendet, um zu berechnen, wie empfindlich die interessierenden Größen in Bezug auf die Eingabeparameter sind. Dieser Studientyp umfasst zwei Methoden: die Sobol- und die Korrelationsmethode.

Die Sobol-Methode analysiert die gesamte Eingabeparameter-Verteilung und zerlegt die Varianz jeder interessierenden Größe in eine Summe der Beiträge der Eingabeparameter und ihrer Wechselwirkungen.

Für jeden Eingabeparameter berechnet die Sobol-Methode die Sobol-Indizes. Der Sobol-Index erster Ordnung gibt die Varianz einer interessierenden Größe an, die auf die Varianz der einzelnen Eingabeparameter zurückzuführen ist. Der Sobol-Gesamtindex gibt die Varianz einer interessierenden Größe an, die auf die Varianz der einzelnen Eingabeparameter und ihre Wechselwirkung mit den anderen Eingabeparametern zurückzuführen ist. Die Sobol-Indizes für jede interessierende Größe und alle Parameter werden in einem speziellen Sobol-Plot dargestellt, in dem die Histogramme nach dem Sobol-Gesamtindex geordnet sind. Die interessierende Größe reagiert am empfindlichsten auf den Eingabeparameter mit dem höchsten Gesamt-Sobol-Index. Die Differenz zwischen dem Gesamt-Sobol-Index und dem Sobol-Index erster Ordnung für einen Eingabeparameter misst die Wirkung der Wechselwirkung zwischen dieser Eingabe und anderen.

Im Vergleich zur Screening-Methode wird die Sensitivitätsanalyse verwendet, um quantitativ zu analysieren, wie sich die Unsicherheiten in den interessierenden Größen auf die verschiedenen Eingabeparameter aufteilen. Diese Methode erfordert mehr Rechenressourcen, da die Berechnung genauer Sobol-Indizes von einem qualitativ hochwertigen Surrogatmodell abhängt.

Bei der Korrelationsmethode wird die lineare und monotone Beziehung zwischen den einzelnen Eingabeparametern und den interessierenden Größen berechnet. Für die Sensitivitätsanalyse auf der Grundlage der Korrelationsmethode werden vier Arten von Korrelationen berechnet: bivariate, nach Rang geordnete bivariate, partielle oder nach Rang geordnete partielle Korrelationen.

Zuverlässigkeitsanalyse

Im Vergleich zu anderen Studienarten zur Unsicherheitsquantifizierung, die die Gesamtunsicherheit der interessierenden Größen untersuchen, befasst sich die Reliability analysis, EGRA-Methode mit einer direkteren Frage. Wie hoch ist die Wahrscheinlichkeit, dass ein Design bei gegebenen unsicheren Eingaben versagt? Das Versagen kann ein vollständiges Versagen des Designs sein, es kann aber auch in Form eines Qualitätskriteriums formuliert werden.

Um die Zuverlässigkeit zu gewährleisten, werden bei der Modellierung und Simulation traditionell Sicherheitsmargen und Worst-Case-Szenarien verwendet. Mit einer angemessenen Zuverlässigkeitsanalyse lassen sich Über- und Unterschätzungen vermeiden, da die tatsächliche Wahrscheinlichkeit abgeschätzt werden kann. Eine grobe Schätzung kann aus der Konfidenzintervalltabelle der Unsicherheitsfortpflanzung für jede interessierende Größe gezogen werden. Mit der Zuverlässigkeitsanalyse können Sie jedoch anspruchsvollere Zuverlässigkeitskriterien auf der Grundlage von Kombinationen der interessierenden Größen und entsprechender Schwellenwerte definieren. Die Methode der effizienten globalen Zuverlässigkeitsanalyse (Efficient Global Reliability Analysis, EGRA), die für die Studie zur Zuverlässigkeitsanalyse verwendet wird, lenkt die Rechenressourcen effizient auf den Grenzzustand, welcher das Versagen und den Erfolg des Designs trennt.

Inverse Unsicherheitsquantifizierung

Die inverse Unsicherheitsquantifizierung (inverse UQ) wird verwendet, wenn einige der Eingabeparameter unbekannte Wahrscheinlichkeitsverteilungen haben. Diese Parameter werden als Kalibrierungsparameter bezeichnet. Mit der inversen UQ können experimentelle Daten rückwärts propagiert werden, um einen Einblick in die statistischen Eigenschaften der Kalibrierungsparameter zu gewinnen. Für die Anwendung der inversen UQ ist eine Wahrscheinlichkeitsverteilung für jeden Kalibrierungsparameter erforderlich, bevor die Analyse durchgeführt werden kann.

Für die Größen von Interesse und die in den Experimenten verwendeten Parameter sind in der Regel experimentelle Daten verfügbar. Es gibt auch Kalibrierungsparameter, die nicht direkt gemessen werden können. Nehmen wir zum Beispiel ein Experiment, bei dem wir den Elastizitätsmodul eines mechanischen Bauteils kalibrieren möchten. Wir können ein Experiment durchführen, bei dem die Zugspannung in Abhängigkeit von der angegebenen Materialverschiebung gemessen wird. Anschließend können eine inverse UQ-Studie durchgeführt und die experimentellen Daten und das Vorwissen über den Elastizitätsmodul verwendet werden, um die Wahrscheinlichkeitsverteilung zu kalibrieren, die die gemessenen Werte der Zugspannung aus den Experimenten am besten wiedergibt. Die inverse UQ kann auf eine Vielzahl von physikalischen Modellen angewendet werden, z.B. in den Bereichen Strukturmechanik, Strömung, Akustik, Wärmetransport, Elektromagnetik und Chemietechnik.

Um die Berechnung der posterioren Wahrscheinlichkeitsverteilungen der Kalibrierungsparameter zu ermöglichen, wird ein Surrogatmodell zusammen mit einer Markov-Chain-Monte-Carlo- (MCMC-) Methode verwendet. Nach der Berechnung können die gemeinsamen Wahrscheinlichkeitsverteilungen und Randverteilungen der kalibrierten Eingabeparameter visualisiert werden. Darüber hinaus wird eine Konfidenzintervalltabelle erstellt, die Informationen wie den Mittelwert, die Standardabweichung, den Minimal- und Maximalwert sowie die Unter- und Obergrenze für die Konfidenzniveaus von 90 %, 95 % und 99 % für jeden kalibrierten Eingabeparameter enthält.