Wie werte ich singuläre Spannungsfelder aus?

Eine der häufigsten Fragen, die wir erhalten, lautet: Wie kann man Spannungen in Gegenwart von Singularitäten am besten auswerten? Die genaueste Antwort ist, dies zu vermeiden. Für die praktische Arbeit ist das jedoch wenig hilfreich. In diesem Blog-Beitrag werfen wir einen detaillierten Blick auf die Eigenschaften singulärer Spannungsfelder und diskutieren einige mögliche Ansätze.

Dies ist eine Fortsetzung unseres Blog-Beitrags Singularitäten in Finite-Elemente-Modellen: Der Umgang mit den roten Flecken, der beschreibt, wann und warum singuläre Spannungen in Strukturmechanik-Modellen auftreten. Er bietet eine allgemeine Einführung in Singularitäten und wir empfehlen ihn als Ausgangspunkt, wenn dieses Thema neu für Sie ist. Detaillierte Informationen über den Umgang mit singulären Spannungsfeldern finden Sie hier.

Singuläre Spannungsfelder

Beginnen wir mit einer detaillierteren Analyse von singulären Spannungsfeldern und ihrer Beziehung zu Spannungskonzentrationen. Es gibt insofern Ähnlichkeiten, als dass eine Spannungskonzentration auch an einer geometrischen Diskontinuität auftritt. Der Unterschied zwischen einer Spannungskonzentration und einer Singularität besteht darin, dass im ersten Fall die maximale Spannung begrenzt ist. Sie können zum Beispiel einen genauen Wert erhalten, indem Sie in einem Finite-Elemente-Modell ein ausreichend feines Netz verwenden.

Normalerweise versuchen Konstrukteure, die Spannungskonzentration zu reduzieren, indem sie eine Verrundung mit einem möglichst großen Radius einführen. Die Spitzenspannung bei einer Spannungskonzentration wird in der Regel als das Produkt aus einem Spannungskonzentrationsfaktor K_{\mathrm t} und einer geeignet gewählten Nennspannung beschrieben. Für eine Verrundung kann manchmal der folgende Ausdruck für K_{\mathrm t} verwendet werden:

 
Dabei ist \rho der Verrundungsradius und L_\mathrm{char} eine charakteristische Länge der Kerbe, die in der Verrundung endet.

Der Hintergrund der Gleichung ist die analytische Lösung für die Spannungskonzentration an einem elliptischen Loch in einer großen Platte, wobei L_\mathrm{char} die Länge der größeren Halbachse der Ellipse ist.

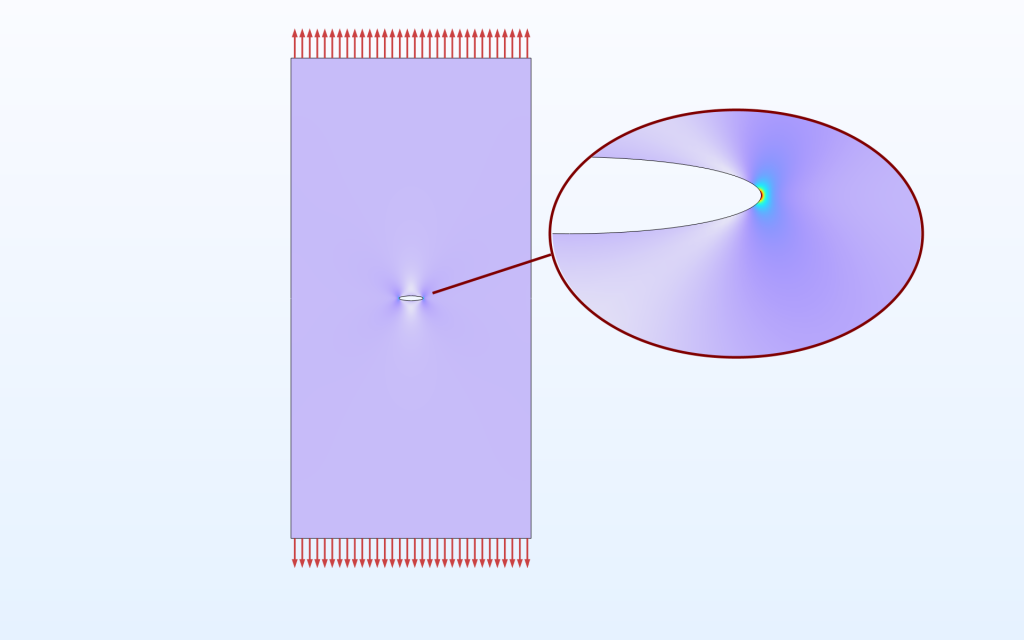
Eine große Platte mit einem elliptischen Loch.

Für die meisten Kerben kann dieser Ausdruck nur verwendet werden, um grobe Schätzungen für K_{\mathrm t} zu liefern, da es schwierig ist, die charakteristische Länge abzuleiten. Die Bedeutung liegt in der Tatsache, dass die maximale Spannung an einer kleinen Kerbe im Wesentlichen proportional zum Kehrwert der Quadratwurzel aus dem Verrundungsradius ist. Jeder Ingenieur, der schon einmal versucht hat, eine lokale Spannungskonzentration zu verringern, hat wahrscheinlich mit dieser Tatsache zu kämpfen gehabt, denn eine moderate Erhöhung des Verrundungsradius führt zu einer noch moderateren Verringerung der maximalen Spannung.

Die ultimative Spannungskonzentration tritt an einer Rissspitze auf, wo der Kerbradius unendlich klein ist. In einem elastischen Festkörper sind die Lösungen für die Spannungs- und Dehnungsfelder in der Nähe der Rissspitze gut bekannt. Sie sind umgekehrt proportional zu der Quadratwurzel aus dem Abstand von der Rissspitze, r. Das Spannungsfeld wird üblicherweise wie folgt beschrieben:

 
Dabei sind K_I, K_{II} und K_{III} die Spannungsintensitätsfaktoren für Modus I (Rissöffnung), Modus II (Längsscherung) bzw. Modus III (Querscherung). Die Funktionen f, g und h bestehen aus trigonometrischen Funktionen des Polarwinkels um die Rissspitze, \theta. (Detaillierte Definitionen finden Sie hier.)

Eine verblüffende Schlussfolgerung ist, dass das Spannungsfeld um eine Rissspitze gleich aussieht, unabhängig von der tatsächlichen Form des Risses sowie der Komponente, in der er existiert, so lange man nahe genug an der Rissspitze ist.

Unter den Annahmen der linear-elastischen Bruchmechanik ist das Kriterium für den Bruch im Modus I K_I = K_{Ic}, wobei K_{Ic} ein Materialparameter ist (genannt Bruchzähigkeit). Auf diese Weise ist es möglich, Geometrien mit dieser speziellen Art von Singularität zu untersuchen, ohne explizit die unendlichen Spannungen zu verwenden. Diese Idee wird im Folgenden generalisiert.

Betrachten Sie nun einen Fall, in dem die Geometrie etwas aufweist, das fast eine Singularität ist. Das heißt, eine Ecke oder ein Riss mit einem kleinen Verrundungsradius. Dies ist das Szenario, auf das wir uns in diesem Blog-Beitrag konzentrieren werden. Aus der Ferne können wir den Unterschied zwischen einer Kerbe und einer Singularität nicht wirklich erkennen. Das folgende Beispiel wird Ihnen die Bedeutung dieser Aussage verdeutlichen.

Es wird ein 2D-Modell eines langen, gekerbten Blechs unter Spannung verwendet. Durch Hinzufügen von Symmetriebedingungen entlang der linken vertikalen Kante kann dasselbe Modell auch für die Untersuchung eines Schlitzes verwendet werden.

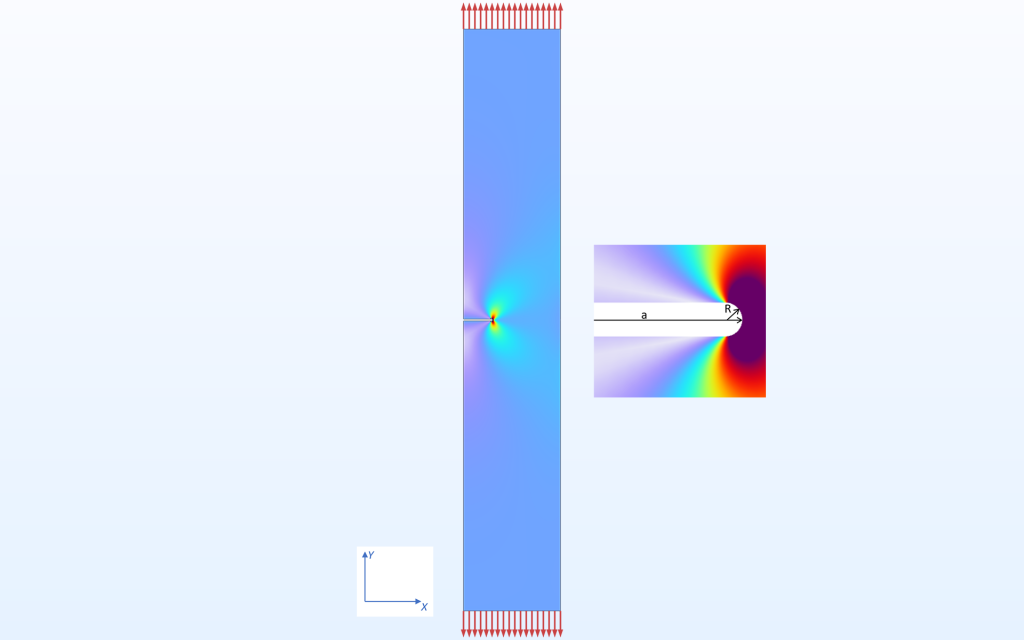
Spannungsverteilung in dem gekerbten Blechstreifen. Das Modell ist in Bezug auf die Kerbtiefe
(a) und dem Kerbradius (R) parametrisiert.

Zunächst können wir feststellen, dass für einen scharfen Riss der Spannungsintensitätsfaktor für diese Geometrie wie folgt geschrieben werden kann:

 
Dabei ist a die Risslänge; \sigma ist die aufgeprägte Spannung (in diesem Fall 1 Pa); und W ist die Breite des Blechstreifens. Es gibt mehrere Darstellungen der Funktion f. Hier werden wir den folgenden Ausdruck verwenden:

 
Dieser Ausdruck ergibt das, was in diesem Blog-Beitrag die Risslösung genannt wird.

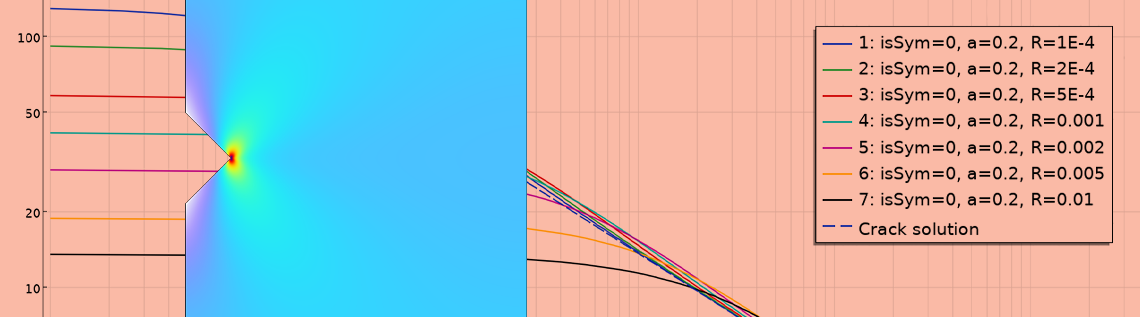
Die Spannungsverteilung, in x-Richtung von der Kerbspitze ausgehend, ist für eine kurze Kerbe und mehrere verschiedene Kerbradien abgebildet. Aufgrund der Symmetrie ist nur eine Spannungskomponente, c, ungleich Null.

Vertikale Spannung entlang der Bauteilbreite als Funktion des Abstands von der Kerbspitze für verschiedene Kerbradien. Die gestrichelte Linie zeigt den theoretischen Wert für einen Riss mit der gleichen Tiefe.

Eine interessante Beobachtung ist, dass das Spannungsfeld in einem bestimmten Regime dem für die Risslösung erhaltenen Feld sehr ähnlich ist. Das heißt, die gerade Linie im Diagramm log(Spannung) gegen log(Abstand). Näher an der Kerbe ist die Spannung begrenzt, da es sich um eine Kerbe und nicht um einen Riss handelt. Wie erwartet, ist die Spitzenspannung proportional zu 1/\sqrt{R}.

Weit von der Spitze entfernt ist die lokale Spannungsfeldlösung für einen Riss ohnehin nicht gültig, unabhängig davon, ob es sich um einen Riss oder eine Kerbe handelt. Aber in dem Bereich zwischen sehr nah und weit entfernt ist es sowohl aus unserer visuellen Perspektive als auch aus der Perspektive der Physik und Mathematik nicht wirklich möglich, die wahre Form der Kerbspitze abzuleiten.

Warum ist das also wichtig? Wenn wir die Form der Kerbe kennen, können wir tatsächlich die Spannung an dieser Stelle bestimmen, indem wir einfach die Spannung in einem bestimmten Abstand betrachten. Wir werden diese Idee später noch genauer beleuchten.

Als nächsten Schritt werden wir die Spannung für eine große Anzahl verschiedener Kerbradien und Kerblängen im selben Diagramm plotten. Die horizontale Achse ist nun jedoch auf den Kerbradius, R, normiert.

Vertikale Spannung entlang der Bauteilbreite als Funktion des Abstands von der Kerbspitze für verschiedene Tiefen und Radien der Kerbe.

Wie Sie hier sehen können, tritt der Zustand der konstanten Steigung in einem Abstand von der Kerbspitze ein, der kleiner ist als der Radius der Spitze, beispielsweise 0,7 R. Aus der Perspektive der Probleme, die wir betrachten, ist das ziemlich nah. Wie lang ist nun dieser Bereich? Das wird nicht durch die Details der Kerbe bestimmt, sondern durch die Größe der Geometrie. Wenn Sie eine andere Normalisierung des Plots verwenden, nämlich die ungeschwächte Bauteilbreite (W-a), erhalten Sie diese Information.

Der gleiche Plot wie oben, aber mit einer Normalisierung des Abstands durch Breite des Restquerschnitts.

Die Schlussfolgerung ist, dass sich das Regime der konstanten Neigung für diesen Fall auf etwa 10% der Breite des Restquerschnitt erstreckt. Weiter entfernt wird das Spannungsfeld nicht mehr durch die Risslösung, sondern durch globalere Eigenschaften gesteuert. Wie groß dieser Bereich für eine bestimmte Geometrie ist, hängt von der für diese Geometrie spezifischen Längenskala ab.

Untersuchen wir, ob das Spannungsfeld in der Risslösung verwendet werden kann, um die maximale Spannung an der Kerbspitze vorherzusagen. Wir beginnen mit dem elliptischen Loch in einer großen Platte. Das Verhältnis zwischen der maximalen Spannung an einem elliptischen Loch (mit Breite a und Kerbradius R) und dem Spannungsintensitätsfaktor für einen Riss (mit Länge a) ist

 
Wenn wir davon ausgehen, dass R << a, dann kann die maximale Spannung durch den Spannungsintensitätsfaktor ausgedrückt werden als

 
Wenn ein Spannungsintensitätsfaktor berechnet werden kann, ist es möglich, die Spannung an einer abgerundeten Rissspitze zu bestimmen, indem man einen Ausdruck wie

 
verwendet, wobei der Koeffizient \beta eine konfigurationsabhängige Zahl in der Größenordnung von 1 ist. Wir können diese Hypothese an dem obigen Beispiel ausprobieren.

In den folgenden Plots wird der Ausdruck

 
als Funktion der Kerbtiefe dargestellt, wobei der Kerbradius als Parameter verwendet wird. Es werden zwei verschiedene Geometrien verwendet: die Randkerbe und ein zentraler Schlitz. Der letztere Fall wird durch das Ergänzen des Modells um eine Symmetriebedingung erreicht.

Der Faktor \beta für den Fall mit einer Randkerbe.

Der Faktor \beta für den Fall mit einem zentralen Schlitz.

Wie Sie sehen können, liegt der tatsächliche Wert des angenommenen Multiplikators \beta in beiden Fällen nahe bei 1,2, solange der Kerbradius klein ist. Bei großen Kerbradien und kleinen Kerblängen ist die Ähnlichkeit mit einem Riss gering. Die Vereinfachung mit R << a ist nicht gültig.

Zur Erstellung dieser Diagramme wurde der analytische Wert von K_I verwendet. In einem realen Fall, in dem er nicht bekannt ist, können die Lösungen in einem Abstand von der Kerbe verwendet werden, um K_I numerisch zu bestimmen.

Tatsächlich gibt es in jeder scharfen Ecke einen Bereich, in dem das Spannungsfeld mit r^{-p} abnimmt, wobei r die Entfernung von der Ecke ist. Bis jetzt haben wir gesehen, dass der ideale Riss p = 0,5 hat. Der Wert von p für einen beliebigen Öffnungswinkel ist im folgenden Diagramm dargestellt.

Stärke der Spannungsabfall-Singularität für verschiedene Öffnungswinkel. Die Werte für 45^°, 90^°, und 135^° sind hervorgehoben.

Die Kurve wurde durch Lösen der transzendenten Gleichung \sin \left ((1-p)(2\pi-\alpha) \right) +(1-p) \sin(2\pi-\alpha) = 0 gezeichnet, wobei \alpha der Öffnungswinkel ist.

Der Vollständigkeit halber können wir die Lösung der transzendenten Gleichung in einem FE-Modell eines unter Spannung stehenden Blechstreifens mit Eckausfräsung überprüfen. Das Modell wird über den Öffnungswinkel der Ecke parametrisiert.

Die Von-Mises-Spannung in dem Modell mit der Eckausfräsung für den Fall, dass der Öffnungswinkel 90^° beträgt.

Vertikale Spannung entlang des Restquerschnitts. Der Abstand von der Spitze der Ecke ist durch die Restquerschnittsbreite normalisiert. Die gestrichelten Linien zeigen die theoretischen Lösungen unter Verwendung der p-Werte von oben.

Wie Sie sehen können, gibt es Regime mit fast geraden Linien im Spannungs-Abstands-Diagramm, die in der Nähe der Ecke gut mit den theoretischen Steigungen übereinstimmen.

Eine andere Art von Singularität wird durch eine materielle Diskontinuität verursacht. In der Praxis tritt dieser Fall oft zusammen mit einer geometrischen Singularität auf. Wir beschränken uns hier auf die Untersuchung einer reinen Materialdiskontinuität in einem Stab, der einer Zugbelastung ausgesetzt ist.

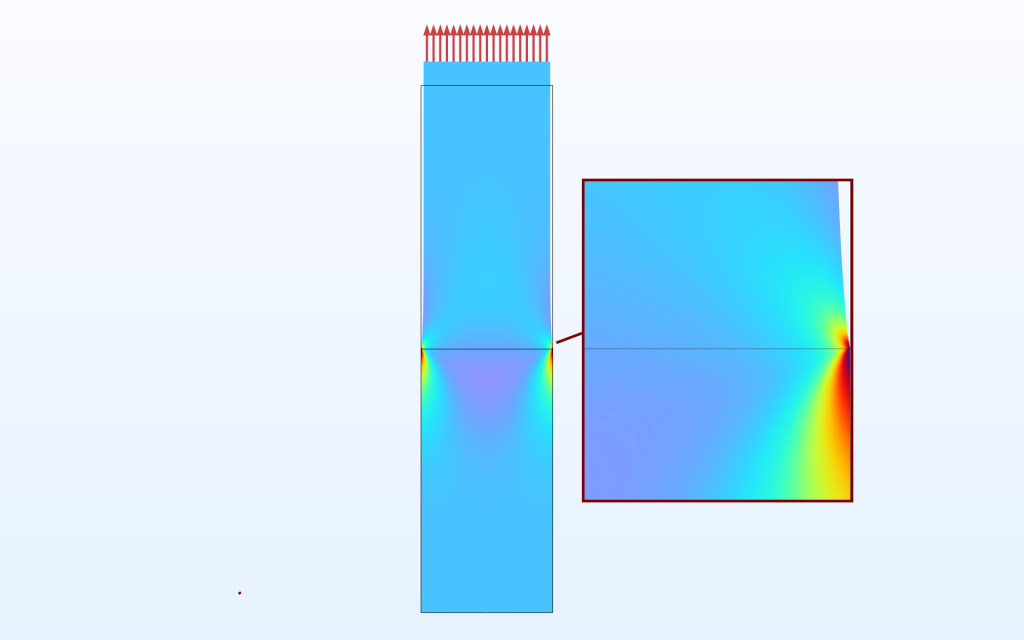
Ein Stab, bei dem der untere Teil steifer ist als der obere Teil. Die Spannung in der Belastungsrichtung wird geplottet.

Einige allgemeine Eigenschaften können bereits in diesem ersten Plot festgestellt werden:

• Eine Singularität entsteht auf der freien Oberfläche.
• Die Spannung im steifen Material ist höher als an der entsprechenden Stelle im weicheren Material.

Um dies genauer zu untersuchen, können wir Diagramme erstellen, die den Abbau der Spannung als Funktion des Abstands von der Materialgrenzfläche zeigen.

Spannung in Belastungsrichtung, geplottet entlang der freien Ränder als Funktion des Abstands zur Grenzfläche. Die durchgezogenen Linien zeigen die Ergebnisse für das weiche Material, während die gestrichelten Linien die Ergebnisse für das steife Material zeigen. Der Parameter r ist das Verhältnis zwischen den beiden Elastizitätsmodulen.

Auch hier können wir im log-log-Diagramm gerade Linien erkennen, die darauf hinweisen, dass die Spannung mit dem Abstand als r^{-p} variiert. Die Stärke ‘p’ ist in beiden Materialien gleich (durchgezogene und gestrichelte Linien derselben Farbe sind parallel). Die Stärke der Singularität wird sowohl durch das Verhältnis zwischen den beiden Elastizitätsmoduln als auch durch die Werte der Poissonzahl gesteuert.

Wenn Sie sich die (übertriebene) deformierte Form im obigen Plot ansehen, kann dies physikalisch interpretiert werden: Das weichere Material wird sich bei gleicher Belastung mehr dehnen als das steifere Material. Das heißt, dass die Dehnungen in Belastungsrichtung größer werden, wenn das Material weich ist. Das bedeutet auch, dass es eine entsprechend größere Kontraktion in der Querrichtung gibt, da die beiden Materialien die gleiche Poissonzahl haben. Diese Kontraktion wird jedoch an der Grenzfläche zwischen den beiden Materialien gehemmt, was zu einer lokalen Spannungssingularität führt.

Wenn wir

 
wählen, verschwindet die Singularität vollständig.

Die Schlussfolgerung ist, dass ein Materialübergang in den meisten Fällen eine Singularität verursacht. Außerdem gibt es in diesem Fall eine Region in der Nähe der Diskontinuität, in der die Spannung nach einem Potenzgesetz abfällt.

Wir haben nun die häufigsten Arten von Singularitäten untersucht, die bei der FE-Modellierung auftreten, und haben festgestellt, dass sie eine gemeinsame Eigenschaft haben: Die Spannungen in der Nähe der Singularität haben eine Potenzgesetz-Abhängigkeit vom Abstand.

Bewertung von Schweißnähten

Die Konstruktion von Schweißnähten, bei denen es nicht zur Ermüdung kommt, ist ein wichtiger Bereich im Ingenieurwesen. Es wurden große Anstrengungen unternommen, um systematische Methoden zur Vorhersage von Ausfällen zu entwickeln, obwohl eine genaue Spannungsbewertung im Allgemeinen unmöglich ist. In diesem Fall liegt das Problem hauptsächlich darin, dass die tatsächliche Geometrie der Schweißnaht unbekannt ist. Je nach der genauen lokalen Geometrie kann die Schweißnaht auch eine Spannungssingularität hervorrufen oder nicht. Um die Sache noch komplizierter zu machen, gibt es oft versteckte Defekte in der Schweißnaht. Die Ausnahme besteht, wenn eine hohe Qualität erforderlich ist. In diesem Fall kann die Schweißnaht geschliffen und mit einer zerstörungsfreien Prüfmethode kontrolliert werden. Aber in den meisten Fällen ist es nicht sinnvoll, eine detaillierte lokale Spannungsanalyse der Schweißnaht durchzuführen.

Eine Kehlnaht, aber mit drei verschiedenen lokalen Geometrien.

Eine Einführung in die Spannungsbewertung von Schweißnähten finden Sie in unserem Blog-Beitrag “How to Predict the Fatigue Life of Welds”.

Anstatt sich mit den Details der Schweißnahtanalyse zu befassen, ist hier eher die Designphilosophie interessant:

• Berechnen Sie die Spannungen an einer genau definierten Stelle, nicht an der Schweißnahtkante selbst.
• Legen Sie die zulässigen Werte für diese Spannung fest. Dies muss in der Regel experimentell erfolgen.
• Der zulässige Spannungswert hängt davon ab, wie und wo Sie sich darauf geeinigt haben, die Spannungen zu bewerten, es handelt sich also nicht um eine echte Materialeigenschaft.

Damals, als man noch mit Stift und Papier rechnete, wurden alle lokalen Effekte ignoriert. Die zulässigen Spannungswerte mussten dem Rechnung tragen und waren daher niedrig. Die modernen FE-basierten Ansätze berücksichtigen einen Teil der Spannungskonzentration (den Teil, der durch die globale Geometrie und nicht durch die lokale Schweißnahtgeometrie verursacht wird). Die Spannungen können dann zwar höher sein, aber immer noch deutlich niedriger als das, was eine reine Materialprüfung ergeben würde.

Im Sinne der Finiten Elemente liefert ein Schalenmodell in der Regel die Spannungen, nach denen Sie suchen, während ein Festkörpermodell Spannungsdetails erfasst, die Sie bei der Durchführung einer Ermüdungsanalyse von Schweißnähten nicht brauchen.

Empfehlenswerte Ansätze

Es gibt einige grundlegend verschiedene Gründe, warum Ihr FE-Modell Singularitäten enthalten kann. Zum Beispiel:

• Die Randbedingungen führen zu Singularitäten, wie sie in dem bereits erwähnten Blog-Beitrag besprochen werden. Wenn eine solche Singularität ein Problem für die Analyse darstellt, kann sie durch Verfeinerung der Randbedingungen gelöst werden.
• Eine scharfe Ecke wird eingeführt, weil die lokale Geometrie einen solchen Maßstab hat, dass es nicht sinnvoll ist, eine Verrundung auf der globalen Skala zu modellieren. In diesem Fall handelt es sich nicht um eine echte Singularität, sondern um eine wohldefinierte Spannungskonzentration. Der genaueste Ansatz ist die Verwendung der Submodellierung, um den lokalen Spannungszustand anhand der globalen Lösung zu bestimmen. Im globalen Modell können Sie die Amplitude des nach dem Potenzgesetz abfallenden Spannungsfeldes in der Nähe der Spannungskonzentrationen verwenden, um zu wissen, worauf Sie Ihre Bemühungen konzentrieren müssen. Eine andere Möglichkeit besteht darin, das Wissen über das Spannungsfeld im Nahfeld mit dem Wissen darüber zu kombinieren, wie es mit einer lokalen Spannungskonzentration korreliert, um zu einer Schätzung dieser lokalen Spannungskonzentration zu gelangen.

Sie können das Muster aus der Schweißnahtbewertung nutzen und es an Ihre lokalen Bedingungen anpassen. Dazu brauchen Sie eine breite Basis an Erfahrungen, auf die Sie aufbauen können. Welche der früheren Designs sind gescheitert und welche nicht? Dann müssen Sie die früheren Designs analysieren und versuchen, eine Bewertungsmethode zu finden, die mit den Erfahrungen korreliert.

Beginnen Sie mit der Erstellung von FE-Modellen dieser Designs und versuchen Sie, eine Region zu identifizieren, in der das Spannungs- oder Dehnungsfeld in dem Bereich liegt, in dem es weder durch die lokalen Kerbdetails noch durch die allgemeinere Geometrie kontrolliert wird. Zumindest während der Entwicklung des Kriteriums kann es notwendig sein, eine Submodellierung anzuwenden.

Welches Kriterium Sie verwenden sollten, ist normalerweise nicht offensichtlich. Da Sie nur relative Vergleiche durchführen und die berechnete Zahl nicht mit einem physikalischen Wert in Beziehung setzen wollen, gibt es viele mögliche Auswahlmöglichkeiten. Hier sind einige Beispiele:

• Die Größe sollte einfach zu bewerten sein.
• Die Größe sollte nicht zu empfindlich auf Unsicherheiten in der Analyse reagieren.
• Wenn möglich, sollte die Größe physikalisch relevant sein. Wenn es sich beispielsweise um ein sprödes Material handelt, ist es vielleicht besser, die größte Hauptspannung oder Hauptdehnung zu betrachten, als ein Vergleichsspannungskriterium wie von Mises zu verwenden.
• Wenn Ermüdung ein Faktor ist, muss die Größe empfindlich gegenüber Lastumkehrungen sein.
• Wenn möglich, wählen Sie ein Dehnungskriterium und kein Spannungskriterium. Der Grund dafür ist, dass die Dehnungen direkt aus den Verschiebungen berechnet werden. Die Spannungen werden dann anhand einer Kombination aus den Dehnungen berechnet. Das bedeutet, dass sich eine einzige ungenaue Komponente im Dehnungstensor auf alle Elemente im Spannungstensor auswirkt.
• In der Software COMSOL Multiphysics^® können Sie das Feature Safety verwenden, um eine große Anzahl verschiedener Kriterien zu bewerten, einschließlich benutzerdefinierter Kriterien.

In einem allgemeinen Fall ist die Stärke der Singularität nicht bekannt. Wir wissen jedoch, dass die interessante Größe in einer bestimmten Region wie folgt variiert:

 
Die Werte von K und p können durch eine Anpassung nach der Methode der kleinsten Quadrate oder einfach durch Verwendung der Werte in zwei Punkten auf dem geraden Teil der Linie in einem log–log-Diagramm ermittelt werden. Da p als eine Eigenschaft betrachtet werden muss, die für eine bestimmte Art von Singularität konstant ist, kann der berechnete Wert als Kontrolle für die Gültigkeit des Ansatzes verwendet werden.

Wenn p bekannt ist, sollte der Wert von K für eine bestimmte Konfiguration mit einem zulässigen Wert verglichen werden. Dies ist eine Analogie dazu, wie Risse in der Bruchmechanik behandelt werden.

Die Perzentil-Methode

Ein anderer Ansatz zur Ermittlung eines zulässigen Spannungsniveaus besteht darin, eine Referenzspannung als den Wert zu definieren, der in einem bestimmten Bruchteil (z.B. 5%) eines Referenzvolumens überschritten wird. Wenn diese Referenzspannung niedriger ist als der zulässige Wert, wird das Design akzeptiert. Durch diesen Ansatz wird das Problem mit Bewertungen in der Nähe der Singularität vermieden. Es ist nur wichtig, das Volumen zu berechnen, in dem die Referenzspannung überschritten wird, und der Rand dieses Volumens liegt in einiger Entfernung von der Singularität, wo die Lösung gut konvergiert.

Diese Methode erscheint einfach, aber sie erfordert eine gewisse Standardisierung, um angewendet werden zu können. Ein Problem dabei ist die Bestimmung des Referenzvolumens. Wenn das Gesamtvolumen der Struktur verwendet wird, ist es möglich, die Referenzspannung zu verringern, indem man einfach mehr Material in einer Region mit geringer Spannung hinzufügt, was natürlich nicht sinnvoll ist. Das Referenzvolumen muss beispielsweise auf die Größe einer bestimmten Region um die Singularität herum bezogen werden. Ein weiterer Nachteil ist, dass die Optimierungsmethoden möglicherweise die Spannungen so verschieben, dass die Referenzspannung verringert wird, während die Spitzenspannung erhöht wird.

Auch hier ist es nur möglich, ähnliche Strukturen miteinander zu vergleichen.

Lassen Sie uns nun besprechen, wie Sie den Spannungswert mit der Perzentil-Methode berechnen können. In COMSOL Multiphysics^® ist es nicht möglich, den 5%-Spannungswert direkt zu ermitteln. Im Folgenden beschreiben wir drei alternative Methoden.

Methode 1

Wenn nur eine einzige Bewertung benötigt wird, ist die schnellste Option in der Regel, ein paar manuelle Iterationen durchzuführen. Sie erstellen einfach einen Integrationsoperator (sagen wir intop1) und werten einen Ausdruck wie intop1(solid.mises>sRef)/intop1(1) aus. Wenn Sie die Referenzspannung sRef ein paar Mal ändern, werden Sie bald den Wert finden, der dem angegebenen Perzentil entspricht.

Methode 2

Verwenden Sie eine Modellmethode, um Methode 1 zu automatisieren.

Methode 3

Sie können eine zusätzliche Gleichung aufstellen und den Spannungswert berechnen, wie nachfolgend erläutert.

Die zu lösende Gleichung lautet:

 
Hier ist \sigma_\mathrm{c} die berechnete Spannung. Dabei kann es sich um eine Vergleichsspannung wie die von Mises, eine erste Hauptspannung oder eine andere Spannung handeln. Es wäre natürlich möglich, das gleiche Verfahren für ein Dehnungs- oder Energiekriterium zu verwenden. Das Referenzvolumen wird mit V_\mathrm{ref} bezeichnet, und \beta ist das Perzentil. Es wird angenommen, dass der Boolesche Ausdruck innerhalb des Integrals den Wert 1 annimmt, wenn er wahr ist, und den Wert 0, wenn er falsch ist.

Um eine Skalierung zu erhalten, die für Berechnungen einfacher zu handhaben ist, ist es besser, die Gleichung umzuformulieren:

 
Das Integral kann mit einem Integrationsoperator berechnet werden, wie bei der ersten Methode. Eine einfache Möglichkeit, diese Gleichung mithilfe eines Knotens Global Equation zu implementieren, sehen Sie hier:

Leider wird dies nicht funktionieren. Eine Ungleichung ist nicht differenzierbar, daher kann keine Jacobi-Matrix gebildet werden. Die Steifigkeitsmatrix wird nur Nullen für diese Gleichung enthalten. Es ist jedoch möglich, dieses Problem zu umgehen, indem Sie eine manuelle Finite-Differenzen-Ableitung einführen. Der Ausdruck ist langwierig und erfordert ein gewisses Verständnis der gleichungsbasierten Modellierung in COMSOL^®. Eine ausführliche Erklärung finden Sie daher im Abschnitt Zusätzliche Informationen unten.

Nachfolgend finden Sie eine modifizierte globale Gleichung, die das Problem der Suche nach der Spannung löst, die das gewünschte Perzentil ergibt.

Hier ist der benutzerdefinierte Parameter dS ein Spannungsinkrement, das im Abschnitt Zusätzliche Informationen durch \Delta \sigma bezeichnet wird.

Als Beispiel für diesen Ansatz wird dasselbe Beispiel einer gekerbten Platte wie zuvor verwendet. Da das Referenzvolumen unabhängig von der Größe der Platte sein sollte, können wir zum Beispiel einen Kreis um die Kerbe wählen. In diesem Fall kann der Radius des Kreises auf der Grundlage der folgenden charakteristischen Längen der Struktur gewählt werden:

• Breite: 1 m
• Minimale Risslänge: 0,1 m
• Minimale Restquerschnittsbreite: 0,3 m
• Maximaler Kerbradius: 0,01 m

Ein Referenzvolumen, das auf einem Kreis mit dem Radius 0,05 m um die Kerbspitze basiert, ist weit von den Rändern der Struktur, aber auch weit von den Details der Kerbe selbst entfernt.

Das Spannungsniveau, das in 5% des Referenzvolumens für verschiedene Werte der Schlitztiefe und des Kerbradius überschritten wird.

Für alle Werte der Schlitztiefe ist die 5%-Perzentilspannung im Wesentlichen unabhängig vom Kerbradius. Sie reagiert nur auf die Schlitztiefe. Dies entspricht der zugrunde liegenden Idee: Vermeiden Sie Empfindlichkeit gegenüber den Details eines lokalen, möglicherweise singulären Spannungsfeldes. Unabhängig davon, ob eine scharfe Spitze oder eine Verrundung verwendet wird, erhält man das gleiche Ergebnis. Im Wesentlichen liefert dieser Ansatz die gleiche Information wie der Spannungsintensitätsfaktor: Er misst die Intensität der Singularität. Wenn Strukturen mit der gleichen Art von Verrundung verglichen werden, könnte diese Methode ein geeignetes Kriterium liefern.

Zusätzliche Informationen

Der Ausdruck enthält zwei Terme: Der erste bildet das Residuum und der zweite die Jacobi-Matrix. Dies ist eine Lösung, die im Allgemeinen in der fortgeschrittenen Modellierung verwendet werden kann. Wenn zum Beispiel die Erstellung einer exakten Jacobi-Matrix teuer ist, können Sie ähnliche Ausdrücke verwenden, um ein korrektes Residuum zusammen mit einer ungefähren Jacobi-Matrix zu bilden.

Der Operator nojac(expr), der an mehreren Stellen verwendet wird, sorgt dafür, dass für den angegebenen Ausdruck keine Jacobi-Beiträge erzeugt werden.

Der Jacobi-Term wird mit dem Faktor (sRef-nojac(sRef)) multipliziert. Da dieser Ausdruck immer zu Null ausgewertet wird, werden von diesem Teil des Ausdrucks keine Residuen erzeugt. Die Ableitung von sRef nach sich selbst ist einfach 1, und der Rest des Ausdrucks ist ein symmetrischer Finite-Differenzen-Ausdruck der Ableitung,

 
Hier ist \Delta \sigma eine endliche Änderung der Spannung. Sie sollte so klein wie möglich gewählt werden und dennoch die Eigenschaft haben, dass das Volumen, das durch \displaystyle \int_V (\sigma_\mathrm{ref}+\Delta \sigma<\sigma_\mathrm{c}) \; dV berechnet wird, sich deutlich von \displaystyle \int_V (\sigma_\mathrm{ref}<\sigma_\mathrm{c}) \; dV unterscheidet. Ein gutes Niveau liegt vor, wenn die Spannungsänderung über ein Element \Delta \sigma in der Nähe der Isofläche für die resultierende Referenzspannung \sigma_\mathrm{ref} liegt.

Zum Abschluss

Auch wenn es aus theoretischer Sicht unmöglich ist, Gradienten und Flüsse (Dehnungen und Spannungen) an einer Singularität auszuwerten, gibt es systematische Methoden, mit denen Sie sich dem Problem nähern können. Diese Methoden setzen jedoch voraus, dass Sie über genügend experimentelle Ergebnisse verfügen, um eine mit Bedacht gewählte kritische Größe zu interpretieren.

Klicken Sie auf die Schaltfläche unten, um die in diesem Blog-Beitrag verwendeten Modelle herunterzuladen.