Singularitäten in Finite-Elemente-Modellen: Der Umgang mit den roten Flecken

Ihr Finite-Elemente-Modell enthält manchmal Singularitäten, d. h. Punkte, an denen ein Aspekt der Lösung zu einem unendlichen Wert tendiert. In diesem Blogbeitrag werden wir die häufigsten Ursachen für Singularitäten untersuchen, wann und wie diese zu entfernen sind und wie die Ergebnisse zu interpretieren sind, wenn Singularitäten in Ihrem Modell auftauchen. Der Großteil dieser Diskussion bezieht sich zwar auf die Strukturmechanik, aber vergleichbare Phänomene sind auch in vielen anderen Bereichen der Physik zu finden.

Das Problem

In meiner früheren Tätigkeit als Consultant für Strukturanalysen stieß ich manchmal auf das Problem, wie man einem Kunden über lachhaft hohe Spannungsspitzen in einem Finite-Elemente-Modell erklärt. Erfahrene Analytiker wissen, wann Spannungsspitzen ein erwarteter Modellierungseffekt sind und getrost ignoriert werden können. Wenn jedoch die Anforderung gestellt wird, dass die Spannung nirgendwo 70 % der Streckspannung überschreiten darf, kann sich dies dennoch als Problem erweisen. Ebenso wichtig ist die Tatsache, dass die kleinen roten Punkte in den Farbdiagrammen sich nicht immer leicht ignorieren lassen. Daher brauchen wir geeignete Techniken zur Interpretation der Modellergebnisse.

Die scharfe Ecke: Ein Prototyp für eine Singularität

Scharfe Ecken führen bei allen elliptischen partiellen Differentialgleichungen zu einer Singularität in den Ableitungen der abhängigen Variablen. In der Strukturmechanik bedeutet dies, dass die Dehnungen unbegrenzt werden können, da die Freiheitsgrade die Verschiebungen sind. Daher werden in solchen Fällen auch die Spannungen unendlich sein, falls es das Materialmodell zulässt.

Spannungen werden im Großteil aller strukturmechanischen Analysen untersucht. Aus diesem Grund sind Singularitäten in der Strukturmechanik ein größeres Problem als in den meisten anderen Bereichen der Physik. Bei Wärmetransportanalysen beispielsweise ist man viel eher an der Temperatur interessiert als an den lokalen Werten des Wärmestroms, dem Bereich, in dem eine Singularität offensichtlich würde.

Werfen wir einen Blick auf ein Prototyp einer Problemstellung. Bei diesem Prototyp geht es um eine 2 mal 1 Meter große rechteckige Platte mit einem quadratischen Ausschnitt von 0,2 Metern Seitenlänge, die einer reinen Spannung ausgesetzt ist:

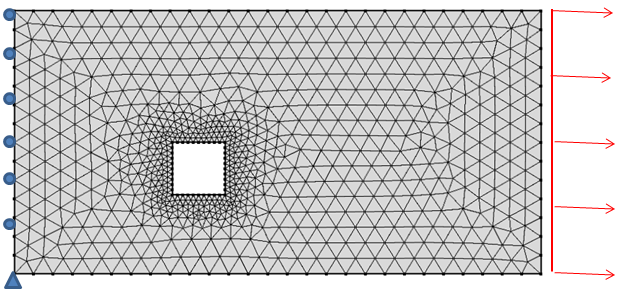
Die Platte ist an der linken Kante eingespannt und hat eine gleichmäßige Belastung an der rechten Kante.

Bei zwei verschiedenen Netzen um das Loch sehen die Standardplots der Vergleichsspannung völlig anders aus. Da die Maximalspannung bei dem Modell mit dem feineren Netz doppelt so hoch ist, gehen die meisten Details im Spannungsfeld verloren. Dies kann natürlich durch manuelles Anpassen des Bereichs der Plots behoben werden, aber auf den ersten Blick können dadurch wichtige Details verborgen bleiben.

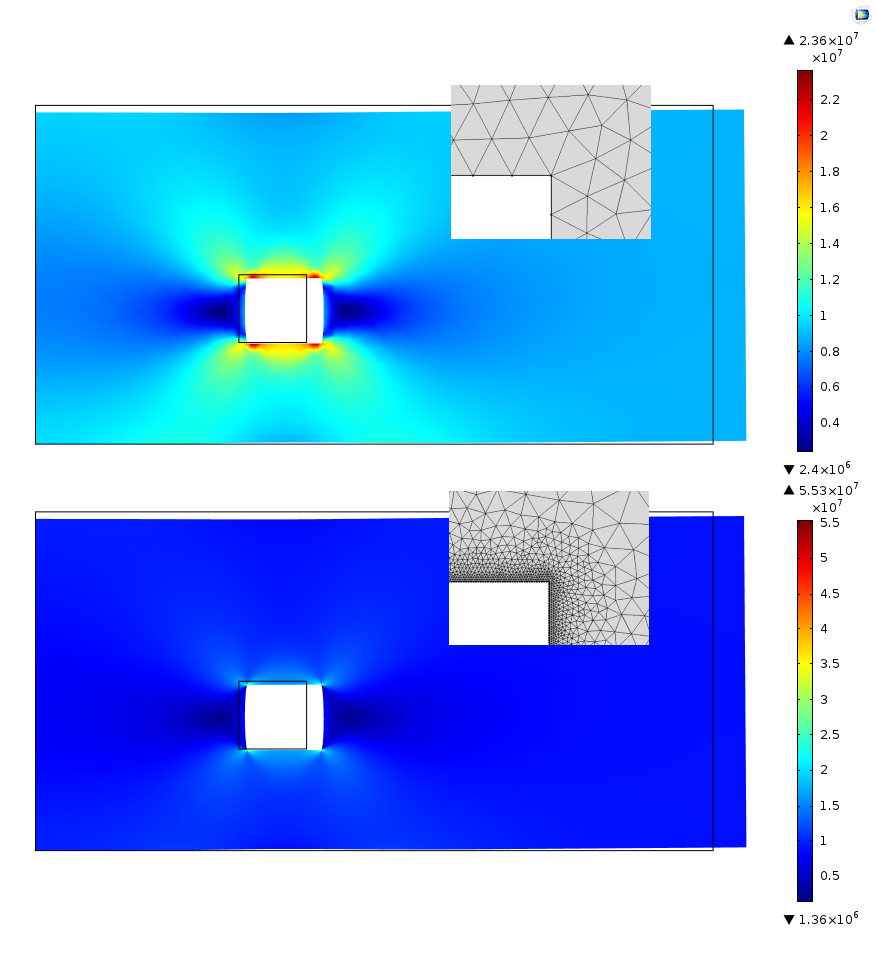
Das selbe Vergleichsspannungsfeld in zwei Plots. Beide Darstellungen sind automatisch um die netzabhängige Spitzenspannung skaliert.

Je kleiner die Elemente sind, die in der Ecke verwendet werden, desto höher sind die gefundenen Spannungswerte. Die Ergebnisse werden nicht konvergieren, da die “wahre” Lösung zu einem unendlichen Wert tendiert.

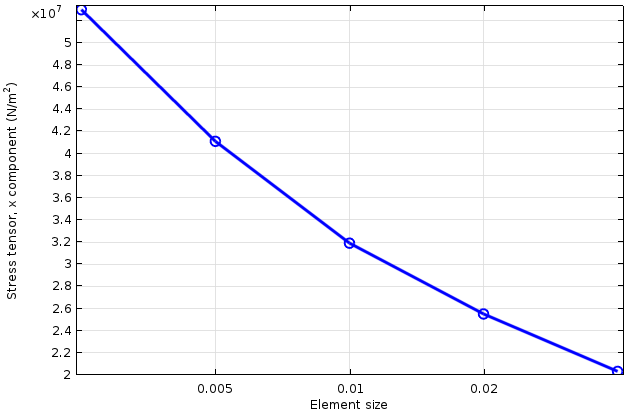
Spannung an der Ecke als Funktion der Elementgröße (logarithmische Darstellung der horizontalen Achse).

Wenn wir das Spannungsfeld in der Nähe des Lochs untersuchen, werden wir feststellen, dass die Spannungsspitze sehr lokalisiert ist. In der folgenden Abbildung ist die Spannung entlang einer vertikalen Schnittlinie aufgetragen, die in einem Abstand von 0,05 Metern vom Loch gezogen wurde. In diesem Abstand ist die Spannung praktisch unverändert, obwohl die Spannungsspitze an der Ecke um den Faktor zwei variiert.

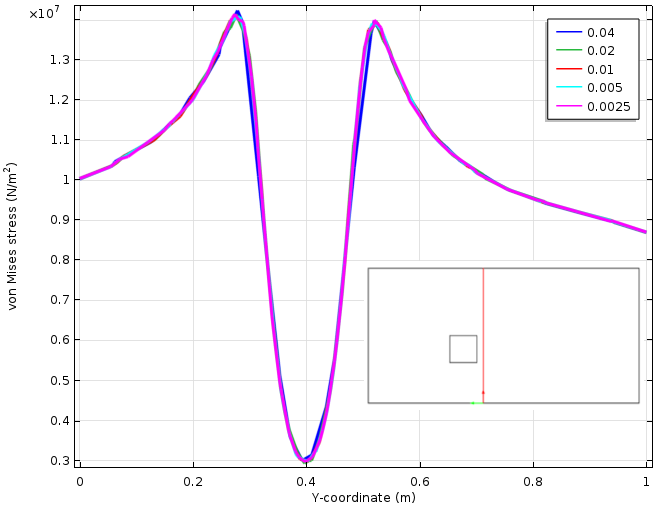
Spannungsverlauf entlang einer Schnittlinie (in rot dargestellt). Es werden fünf verschiedene Netzgrößen verwendet.

In der realen Welt gibt es nur selten perfekt scharfe Ecken. Daher könnte man argumentieren, dass man mit einer korrekten Geometrie, die überall Verrundungen enthält, Singularitäten komplett vermeiden könnte. Das stimmt zwar, hätte aber auch einen Preis: Wenn sehr kleine geometrische Details durch das Netz aufgelöst werden müssen, wird das Modell enorm groß (insbesondere in 3D). Selbst wenn eine perfekte CAD-Geometrie zur Verfügung steht, ist es gängige Praxis, die Geometrie zu defeaturen, um kleine Details zu entfernen, die für die Simulation nicht relevant sind. In vielen Fällen werden daher in der Aufbereitung der Geometrie absichtlich scharfe Ecken eingeführt.

Das Behalten der scharfen Ecke hat jedoch auch einige Nachteile:

• Es kann numerische Probleme geben, wenn das Materialmodell nichtlinear ist. So ist beispielsweise die von einem Kriechmodell vorhergesagte Dehnungsrate oft proportional zu einer hohen Potenz der Spannung. Die hohe Spannung an der Singularität (ein Wert, der nur durch das Netz bestimmt wird), die mit einer Fünferpotenz multipliziert wird, kann zu so hohen Dehnungsraten führen, dass die Zeitschritte in der Größenordnung von Millisekunden liegen müssten, obwohl man eigentlich eine Simulation durchführen möchte, die einige Monate Simulationszeit auflösen soll. Wenn Sie die scharfen Ecke trotzdem beibehalten wollen, besteht die Lösung darin, die Singularität in einen kleinen elastischen Bereich einzuschließen.
• Adaptive Vernetzungen, Fehlerabschätzungen und Ähnliches können fehlschlagen, da die Singularität den Rest der Lösung dominieren wird. Schließen Sie die Ecke von allen derartigen Verfahren aus
• Bei einer Optimierung, bei der Spannungen Teil der Problemformulierung sind, führt die Singularität zu Lösungen, die nur im Hinblick auf die Verringerung der Amplitude der unphysikalischen Spannungsspitze optimal sind. In dem Multistudy Optimization of a Bracket Tutorial ist der Bereich, in dem die Halterung verschraubt ist, von der Auswertung der maximalen Spannung ausgeschlossen.
• Wie bereits erwähnt, neigen die hohen Belastungsspitzen dazu, interessantere Merkmale in der Lösung zu verdecken, sowohl visuell als auch psychologisch.

Wenn die Ecke sehr scharfkantig ist, wird das Material durch die hohen Dehnungen beschädigt. Ein sprödes Material kann brechen, ein duktiles Material kann nachgeben. Dies mag zwar alarmierend klingen, aber in den meisten Fällen führt eine solche Beschädigung nur zu einer lokalen Umverteilung der Spannungen. Aus der Perspektive der umgebenden Struktur ist die Wirkung nicht dramatischer als die einer leichten Änderung des Verrundungsradius. Hohe, lokal begrenzte Spannungen stellen nur dann ein echtes Problem dar, wenn die Belastung zyklisch erfolgt, was ein Risiko darstellt für Ermüdung.

In Gebäuden sorgt sich niemand über die Tatsache, dass die Öffnungen für Fenster und Türen rechteckig sind und scharfe Ecken haben. In Flugzeugen jedoch sind die Fenster glatt abgerundet, da die Schwankungen zwischen dem Druck in der Kabine und dem Außendruck eine zyklische Spannungsbelastung darstellen.

Links: Ein rechteckiges Fenster mit scharfen Ecken. Image by Jose Mario Pires. Licensed under CC BY-SA 4.0 via Wikimedia Commons. Rechts: Ein Fenster mit sanft abgerundeten Ecken. Image by Orin Zebest. Licensed under CC BY-SA 2.0 via Wikimedia Commons.

Dies wird in vielen Designs berücksichtigt, in denen hohe lokale Spannungen zulässig sind, solange die Lasten statisch sind. Die lokalen Eckspannungen wirken sich in keiner Weise auf die Tragfähigkeit der Struktur aus. Die Anwendung eines solchen Ansatzes setzt jedoch eine systematische Klassifizierung der Spannungsfelder voraus. Solche Methoden sind zum Beispiel im ASME Boiler & Pressure Vessel Code beschrieben.

Bei zyklischen Belastungen hingegen ist es wichtig, sehr genaue Spannungswerte zu erhalten. Die Lebenszeit des Bauteils hängt stark von der Spannungsamplitude ab. In diesem Fall ist eine genaue Darstellung der Verrundung erforderlich, nicht nur geometrisch, sondern auch in Bezug auf die Netzauflösung. Falls das Modell dadurch zu groß zum Lösen wird, empfiehlt sich Submodeling, ein Ansatz der im Detail in diesem Blogbeitrag erklärt wird.

Das detaillierte Submodell auf der rechten Seite wird durch die Ergebnisse der globalen Simulation gesteuert.

Tipp: Um tiefer ins Submodeling einzusteigen, laden Sie sich unser Submodeling Analysis of a Shaft Tutorial aus unserer Application Galerie herunter.

Punktuelle Belastungen

Eine Kraft, die auf einen einzigen Punkt eines Festkörpers einwirkt, erzeugt lokal unendliche Spannungen. Das ist das klassische Boussinesq-Cerruti Problem in der Elastizitätstheorie, wo die Spannungen mit dem Kehrwert des Abstands vom belasteten Punkt variieren.

In der realen Welt gibt es keine Punktlasten. Die Kraft ist immer auf einer gewissen Fläche verteilt. Aus der Perspektive einer Finite Elemente Analyse ist die Frage, ob es sich lohnt, diese kleine Region aufzulösen. Die Antwort dieser Frage beruht auf dem Prinzip von Saint-Venant, welches besagt, dass alle statisch äquivalenten Lastverteilungen bei einem im Vergleich zur Größe der belasteten Fläche ausreichend großen Abstand das gleiche Ergebnis liefern.

Wenn also detaillierte Ergebnisse innerhalb eines Abstands von beispielsweise der dreifachen Größe der belasteten Fläche nicht wichtig sind, ist es eigentlich egal, wie Sie die Lasten aufbringen, solange die resultierende Kraft und das Moment korrekt sind. Genau wie im Fall der Eckensingularität müssen Sie möglicherweise die Auswirkungen singulärer Spannungen vermeiden. Beachten Sie, dass Linienlasten die gleiche Wirkung wie eine Punktlast haben, indem sie lokale unendliche Spannungen verursachen.

Erwähnenswert ist auch, dass eine Punktlast, die auf ein Balkenelement oder senkrecht auf einen Flächenelement wirkt, keine Singularität hervorruft. Die Verbiegung struktureller Elemente wird durch andere Gleichungen beschrieben als die der Festkörpermechanik. Eine Punktlast, die in Richtung der Ebene eines Flächenelements aufgebracht wird, führt jedoch wieder zu einer Singularität.

Zwangsbedingungen

Betrachtet man eine Zwangsbedingung im Sinne ihrer Fähigkeit, eine Reaktionskraft aufzubringen, so kann man dieselben Schlussfolgerungen ziehen wie bei Lasten, z. B. bei punktuellen Zwangsbedingungen. Aber das ist noch nicht alles. Betrachten wir das scheinbar symmetrische Problem unten. Hier haben wir eine Platte mit einer konstanten Zugbelastung auf der einen und Gleitbedingungen auf der anderen Seite.

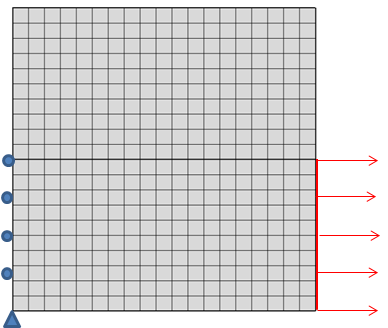
Eine quadratische Platte, bei der die vertikalen Ränder je zur Hälfte eingespannt und belastet sind.

Bei der Betrachtung der Spannungsverteilung wird deutlich, dass am Übergang zwischen der Gleitbedingung und dem freien Rand eine Singularität auftritt, auf der Seite mit der Zugbelastung jedoch nicht. Eine allgemeine Beobachtung ist, dass das Ende einer Zwangsbedingung eine ähnliche Wirkung wie eine scharfe Ecke hat.

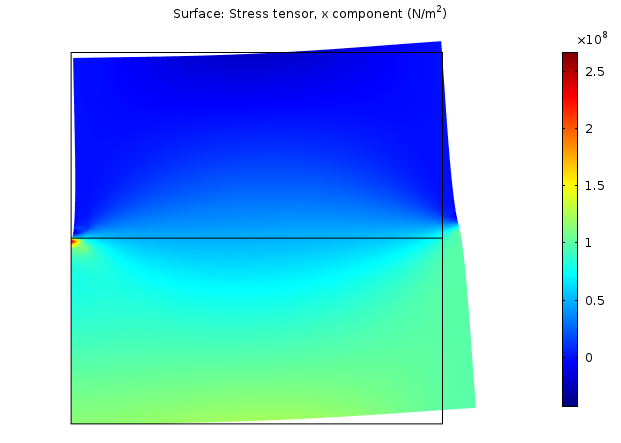
Horizontale Spannungsverteilung.

Eine unendlich starre Umgebung, die die Struktur festhält, gibt es in der Realität nicht. Der Analytiker steht wieder vor der Wahl: Kann ich mit dem kleinen roten Fleck leben, oder muss ich dem, was außerhalb meiner Struktur liegt, mehr Aufmerksamkeit schenken?

Wenn die durch die Randbedingung verursachte Singularität nicht akzeptabel ist, können Sie die folgenden Ansätze in Betracht ziehen:

• Erweitern Sie das Modell so, dass jede durch die Randbedingung verursachte Singularität aus dem Bereich von Interesse verschoben wird.
• Verwenden Sie eine weichere Randbedingung, indem Sie z. B. eine Spring Foundation-Bedingung anwenden.
• Verwenden Sie Infinite Elemente, die eine kostengünstige Methode zur Erweiterung des Berechnungsbereichs darstellen. Erfahren Sie mehr in diesem Tutorial.

Ähnliche Situationen wie die oben beschriebene sind bei vielen Übergängen unvermeidlich. Ein Beispiel für einen solchen Übergang ist die Verbindung eines starren Bereichs mit einem flexiblen Bereich.

Schweißnähte

Die Kunst der Analyse von Schweißnähten ist so wichtig und komplex, dass sie einen eigenen Blogbeitrag verdient. Wir werden hier nur kurz auf dieses Thema eingehen.

Geschweißte Strukturen bestehen oft aus dünnen Platten, daher ist es naheliegend, in diesem Zusammenhang Flächenmodelle (Shells) zu verwenden. Werfen wir einen Blick auf das unten stehende Modell. In diesem Beispiel ist eine Spannungskonzentration in dem Bereich zu erkennen, in dem die kleinere Platte mit der breiten Platte verschweißt ist.

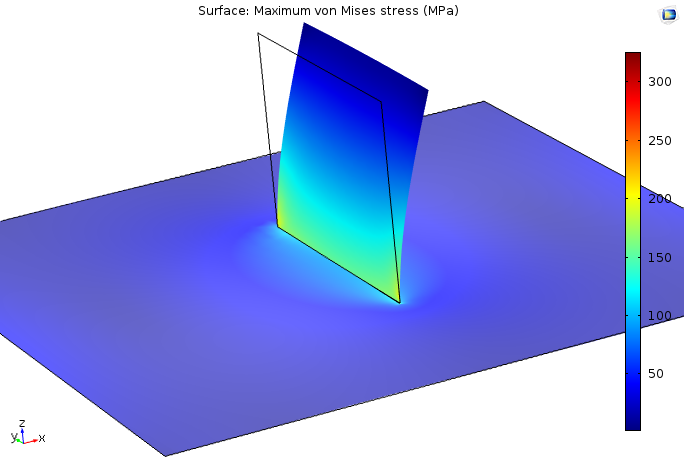
Spannungen in einem einfachen Shell-Modell aus zwei miteinander verschweißten Platten.

Die Geometrie und die Lasten sind symmetrisch in Bezug auf den Mittelpunkt der Geometrie. Das Netz in diesem Modell ist jedoch so ausgelegt, dass es an einem Ende der Schweißnaht viel feiner ist. Ein Spannungsdiagramm entlang der Schweißnahtlinie zeigt eine Singularität im Spannungsfeld beider Platten.

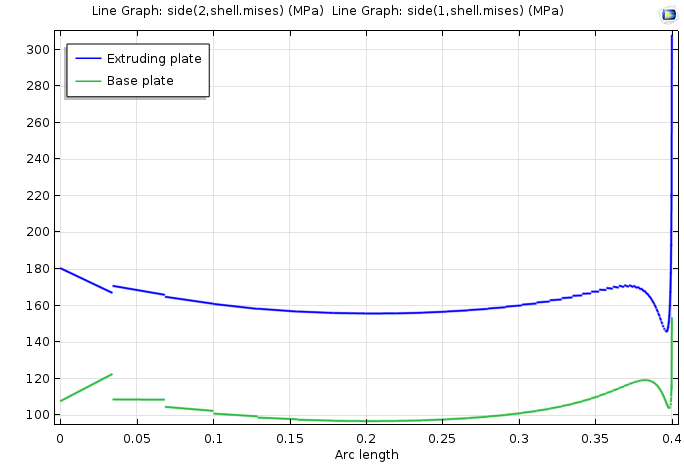
Das Spannungsdiagramm identifiziert eine Singularität.

Für viele geschweißte Strukturen — Schiffsrümpfe, Frachtkräne und LKW-Rahmen — ist das Auslegen gegen Ermüdung wichtig. Die Verbesserung der Simulation durch die Verwendung eines Volumenmodells ist hier nur selten die Lösung. Die lokale Geometrie und Qualität einer Schweißnaht ist selten gut definiert, es sei denn, sie wurde geschliffen und geröntgt. Die lokale Geometrie wird sich entlang der Schweißnaht und zwischen den entsprechenden Schweißnähten zweier Teile, die eigentlich identisch sein sollten, unterscheiden.

Bei der Analyse von Schweißnähten wird in der Regel der Mittelwert der Spannung entlang der Schweißnaht oder entlang einer parallelen Linie in einem bestimmten Abstand gebildet. Die Schnittlinien in COMSOL Multiphysics^® sind hier besonders hilfreich. Die lokalen Koordinatensysteme sind ebenfalls nützlich, da Spannungskomponenten parallel und normal zur Schweißnaht unterschiedlich behandelt werden müssen. Diese gemittelten Spannungen werden dann mit Literaturwerten verglichen, die für eine Reihe von Schweißnahtkonfigurationen und Schweißnahtqualitäten verfügbar sind. Mehr darüber erfahren Sie im Eurocode 3: Design of steel structures — Part 1-9: Fatigue.

Risse

Die denkbar schlechteste geometrische Singularität ist die, die durch einen Riss verursacht wird. Ein Riss kann als eine um 180° gedrehte Ecke betrachtet werden, so dass viele Aspekte der Eckensingularität auch hier anwendbar sind. Wenn ein Riss in einem Finite-Elemente-Modell vorhanden ist, ist er in der Regel ein wesentlicher Aspekt der Studie.

Das Spannungsfeld um eine Rissspitze, wobei die Verformung skaliert ist.

Das Spannungsfeld um die Rissspitze ist aus analytischen Lösungen bekannt, zumindest für lineare Elastizität und Plastizität unter bestimmten Annahmen. Die Berechnung des Spannungsfeldes durch Finite-Elemente-Analyse kann jedoch aufgrund der Singularität schwierig sein. Glücklicherweise ist es in der Regel nicht notwendig, die Details an der Rissspitze zu untersuchen. Bei der Bestimmung des Spannungsintensitätsfaktors können Sie zum Beispiel entweder das J-Integral oder den Energy Release Rate-Ansatz wählen. Diese Methoden verwenden globale Größen weit weg von der Rissspitze, so dass die Details an der Singularität weniger wichtig werden.

Tip: Möchten Sie mehr über die Anwendung des J-Integral-Ansatzes erfahren? Konsultieren Sie das Single Edge Crack tutorial aus unserer Application Galerie.

Fazit

Singularitäten treten in vielen Finite-Elemente-Modellen aus unterschiedlichen Gründen auf. Solange Sie verstehen, wie die Ergebnisse zu interpretieren sind und wie Sie einige der Konsequenzen umgehen können, sollte das Vorhandensein von Singularitäten bei Ihrer Modellierung kein Problem darstellen. Tatsächlich erfordern viele Industrie-Modelle die absichtliche Verwendung von Singularitäten. Um die Modellgröße und den Zeitaufwand für die Analyse zu reduzieren, ist es oft notwendig, geometrische Details, Belastungen und Randbedingungen so zu vereinfachen, dass Singularitäten entstehen.