Nehmen wir an, Sie arbeiten an einem Modellierungsfall, bei dem sich die Lasten so bewegen, dass sie während der Simulation verschiedene Netzelemente und Ränder übertreten. In diesen Fällen möchten Sie vielleicht eine Randbedingung nur auf einen Teil des geometrischen Rands oder nur unter bestimmten Bedingungen anwenden. In diesem Blog-Beitrag werden wir erörtern, wie Sie die Flexibilität von COMSOL Multiphysics® nutzen können, um solche Situationen zu bewältigen.
Kategorisierung von Randbedingungen
Bei der mathematischen Behandlung von partiellen Differentialgleichungen stößt man auf Randbedingungen vom Typ Dirichlet, Neumann und Robin. Bei einer Dirichlet-Bedingung geben Sie die Variable vor, nach der Sie lösen wollen. Mit einer Neumann-Bedingung hingegen wird ein Fluss, d. h. ein Gradient der abhängigen Variablen, vorgegeben. Eine Robin-Bedingung ist eine Mischung aus den beiden vorherigen Randbedingungstypen, bei der eine Beziehung zwischen der Variablen und ihrem Gradienten vorgeschrieben ist.
Die folgende Tabelle enthält einige Beispiele aus verschiedenen Bereichen der Physik, die die entsprechende physikalische Interpretation zeigen.
| Physik | Dirichlet | Neumann | Robin |
|---|---|---|---|
| Festkörpermechanik | Verdrängung | Zug | Feder |
| Wärmetransport | Temperatur | Wärmeströmung | Konvektion |
| Akustik | Akustischer Druck | Normale Beschleunigung | Impedanz |
| Elektrische Ströme | Festes Potential | Fester Strom | Impedanz |
Im Rahmen der Finite-Elemente-Methode haben diese Arten von Randbedingungen unterschiedliche Auswirkungen auf die Struktur des zu lösenden Problems.
Neumann-Bedingungen
Die Neumann-Bedingungen sind “Lasten” und erscheinen auf der rechten Seite des Gleichungssystems. In COMSOL Multiphysics® kann man sie als schwache Beiträge im Equation View sehen. Da die Neumann-Bedingungen rein additive Beiträge zur rechten Seite sind, können sie eine beliebige Funktion von Variablen enthalten: Zeit, Koordinaten oder Parameterwerte.
Betrachten wir ein Wärmetransportproblem, bei dem sich eine kreisförmige Wärmequelle mit einem Radius R mit einer Geschwindigkeit v in die Richtung x bewegt. Ihre Intensität hat eine parabolische Verteilung mit einem Maximalwert q_0. Eine mathematische Beschreibung dieser Belastung könnte sein:
Bei einer wandernden Last ist es offensichtlich nicht möglich, Bereichsränder oder gar ein Netz zu haben, das zu jedem Zeitpunkt der Lastverteilung entspricht.
Die Lastverteilung selbst kann auf einfache Art und Weise eingegeben werden. Da die Variable für die radiale Koordinate, r, an zwei Stellen verwendet wird, ist es sinnvoll, sie als Variable zu definieren. Die gesamte Eingabe für die sich bewegende Wärmequelle ist unten dargestellt.
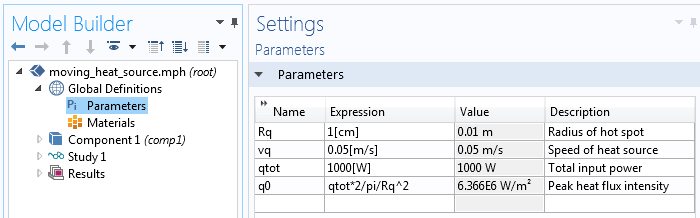
Parameter, die eine sich bewegende Wärmequelle beschreiben.
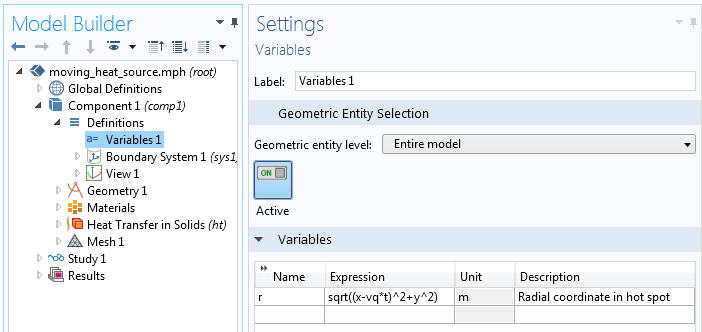
Die Variable, die die lokale radiale Koordinate vom aktuellen Zentrum der sich bewegenden Wärmequelle beschreibt.
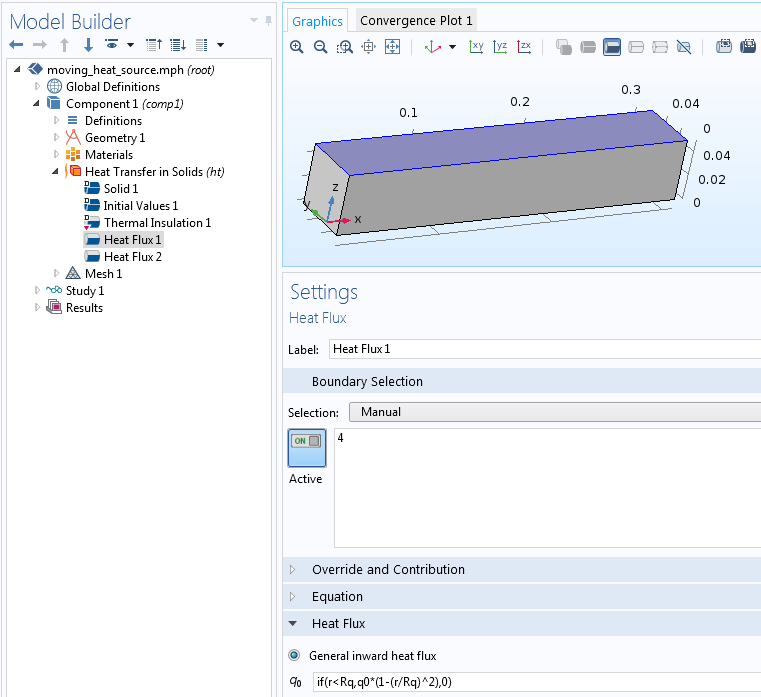
Eingabe der Wärmeströmung.
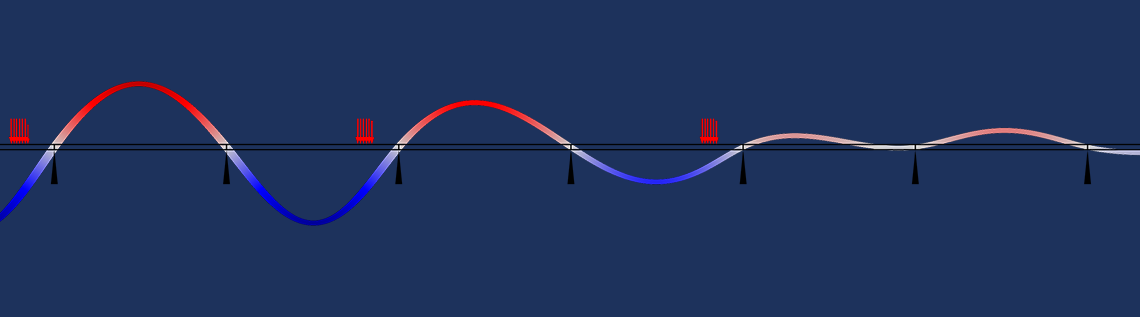
Die Ergebnisse einer zeitabhängigen Simulation mit solchen Daten sind in der folgenden Animation dargestellt. Es wird von einer Symmetrie in der yz-Ebene ausgegangen, so dass die Last tatsächlich auf einen sich bewegenden Halbkreis aufgebracht wird.
Animation der Temperaturverteilung für die sich entlang des Balkens bewegende Wärmequelle.
Dirichlet-Bedingungen
Bei Vorliegen einer Dirichlet-Bedingung ist die abhängige Variable vorgegeben, so dass nicht nach ihr gelöst werden muss. Gleichungen für solche Freiheitsgrade können somit aus dem Problem eliminiert werden. Dirichlet-Bedingungen verändern also die Struktur der Steifigkeitsmatrix. Im Equation View von COMSOL Multiphysics® erscheinen diese Bedingungen als Beschränkungen.
Nehmen wir an, Sie möchten, dass der wandernde Punkt eine Temperatur von genau 450 K vorgibt. Das ist vielleicht etwas künstlich, aber es zeigt einen wichtigen Unterschied zwischen der Neumann-Bedingung und der Dirichlet-Bedingung. Wenn Sie einen Temperature-Knoten hinzufügen und einen ähnlichen Ausdruck eingeben würden ( if(r < R,450[K],0)), würde dies bedeuten, dass die Temperatur auf dem Teil des Randes, der nicht vom Hot Spot abgedeckt ist, auf den absoluten Nullpunkt gesetzt wird.
Die Absicht ist jedoch, die Dirichlet-Bedingung außerhalb des Hot Spots auszuschalten. Hierfür gibt es einen kleinen Trick. Wenn Sie stattdessen if(r < R,450[K],ht.Tvar) als vorgeschriebenen Wert eingeben, erhalten Sie das gewünschte Verhalten (wie in der folgenden Animation gezeigt).
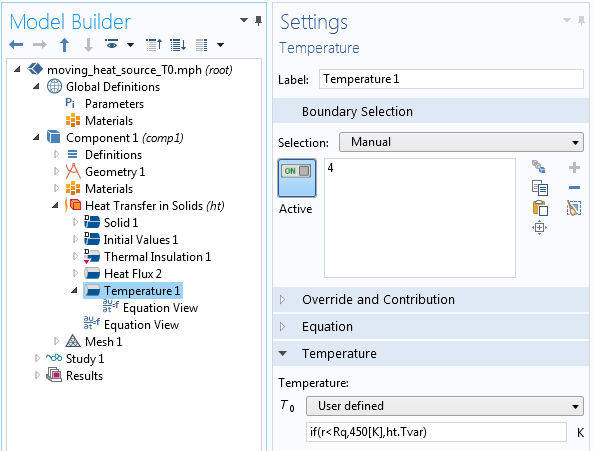
Einstellungen für eine konditionale Dirichlet-Bedingung.
Animation der Temperaturverteilung für einen sich entlang des Balkens bewegenden vorgeschriebenen Temperaturpunkt.
Um zu verstehen, wie das funktioniert, aktivieren Sie den Equation View und sehen Sie sich die Implementierung der Dirichlet-Bedingung an (in diesem Fall eine vorgegebene Temperatur):
Aktivierung des Equation View.
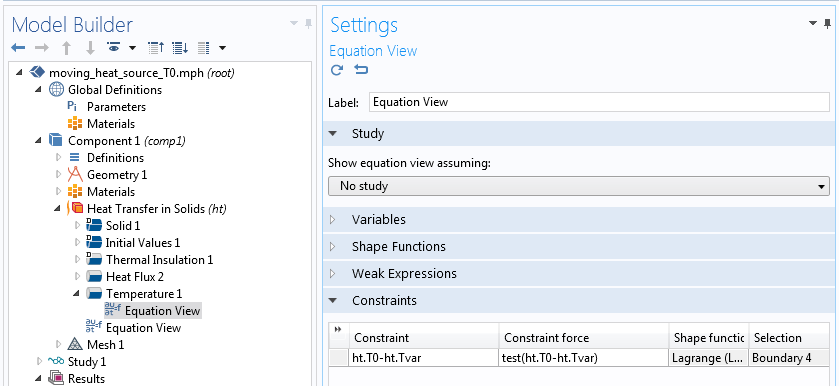
The Equation View für den Temperature -Knoten.
Die Zwangsbedingung wird als ht.T0-ht.Tvar formuliert, was implizit bedeutet, dass ht.T0-ht.Tvar = 0. Der erste Term ist die vorgeschriebene Temperatur, die Sie als Eingabe angeben. Der zweite Term ist nur der Freiheitsgrad der Temperatur, der zu einer Variablen wird. Dadurch wird die Temperatur auf den vorgegebenen Wert beschränkt, es sei denn, der vorgegebene Wert ist die Zeichenkette ht.Tvar. In diesem Fall reduziert die symbolische Algebra während der Zusammenstellung den Ausdruck auf ht.Tvar-ht.Tvar, und weiter auf Null. Und da der Ausdruck 0 ist, gibt es keine Zwangsbedingungen.
Schwache Zwangsbedingungen
In COMSOL Multiphysics® Multiphysics gibt es zwei mögliche Implementierungen einer Dirichlet-Bedingung. Der Standardfall ist pointwise constraint, wie oben beschrieben, aber Sie können auch weak constraint verwenden. Bei der schwachen Zwangsbedingung (weak constraint) werden die Gleichungen hinzugefügt und nicht entfernt. Die Wärmeströme, die benötigt werden, um die vorgeschriebenen Temperaturwerte zu erreichen, werden dann als zusätzliche Freiheitsgrade (Lagrange-Multiplikatoren) hinzugefügt.
Sie können im Wesentlichen denselben Trick anwenden, um eine schwache Zwangsbedingung konditional zu machen, nur mit einer kleinen Änderung. Die Verwendung von schwachen Zwangsbedingungen erfordert, dass Sie zuerst die Advanced Physics Options aktivieren.
Das Aktivieren der Advanced Physics Options.
Wenn in einem Knoten innerhalb eines Physik-Interfaces schwache Zwangsbedingungen ausgewählt wurden, gibt es zusätzliche Freiheitsgrade für den Lagrange-Multiplikator. In unserem Fall hat der Freiheitsgrad den Namen T_lm.
Wenn derselbe Ausdruck für die Temperatur wie oben verwendet wird, erhält der zusätzliche Freiheitsgrad keinen Beitrag zur Steifigkeitsmatrix auf dem Teil des Randes, auf dem die Dirichlet-Bedingung ausgeschaltet ist. Die Steifigkeitsmatrix wird somit singulär. Um diese Situation zu vermeiden, ändern Sie if(r < R,450[K],ht.Tvar) in if(r < R,450[K],ht.Tvar-T_lm*1e-2). Der für T_lm verwendete Multiplikator ist je nach Modell und physikalischem Feld unterschiedlich und muss unter Umständen angepasst werden.
Der Grund dafür, dass dies funktioniert, wird, wie es in einem Lehrbuch heißt, “dem Leser als Übung überlassen”.
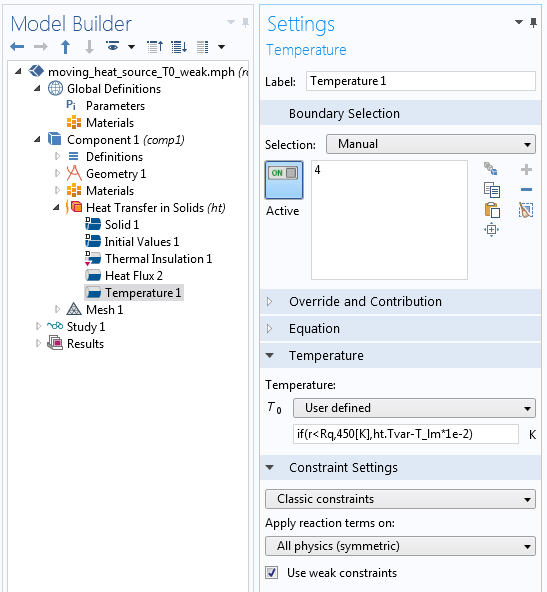
Einstellungen für die konditionale Dirichlet-Bedingung wenn schwache Zwangsbedingungen verwendet werden.
Robin-Bedingungen
Die Robin-Bedingungen tragen im Allgemeinen sowohl zur Steifigkeitsmatrix als auch zur rechten Seite bei. Die Struktur der Steifigkeitsmatrix wird nicht beeinflusst, aber es werden Werte zu bestehenden Positionen hinzugefügt. Die Robin-Bedingungen erscheinen auch als schwache Beiträge im Equation View. Die Umwandlung dieser Bedingungen in Funktionen von Zeit, Raum und anderen Variablen ist nicht anders als bei Neumann-Bedingungen.
Interessant ist jedoch, dass Sie durch die Wahl geeigneter Werte die Robin-Bedingungen so umwandeln können, dass sie annähernd als Dirichlet- oder Neumann-Bedingungen wirken. Dies ist besonders wichtig für Fälle, in denen Sie während einer Simulation zwischen den beiden Randbedingungsarten wechseln möchten.
Um eine Dirichlet-Bedingung zu erstellen, weist man der “Steifigkeit” einen hohen Wert zu, zum Beispiel eine Federkonstante oder einen Wärmeübergangskoeffizienten. Mathematisch gesehen handelt es sich dabei um eine Penalty-Implementierung der Dirichlet-Bedingung. Je höher die Steifigkeit ist, desto genauer ist der vorgeschriebene Wert für den Freiheitsgrad. Es gibt jedoch einen Vorbehalt: Eine sehr hohe Steifigkeit beeinträchtigt die numerische Konditionierung der Steifigkeitsmatrix. Für ein Wärmetransportproblem wäre ein Ausgangspunkt für die Wahl eines “hohen” Wärmeübergangskoeffizienten alpha
wobei \lambda die Wärmeleitfähigkeit und h eine charakteristische Elementgröße ist.
Dieselbe Idee kann auf andere Bereiche der Physik angewandt werden, indem \lambda durch die entsprechende Materialeigenschaft ersetzt wird (z. B. das Elastizitätsmodul in der Festkörpermechanik). Der Faktor 1000 ist nur ein Vorschlag und kann durch 104 oder 105 ersetzt werden.
Wenn Sie den sich bewegenden Punkt von 450 K aus dem vorherigen Beispiel mit Konvektion modellieren wollen, können Sie die unten gezeigten Einstellungen verwenden. Die eingebaute Variable h für die Elementgröße wird in dem Ausdruck verwendet.
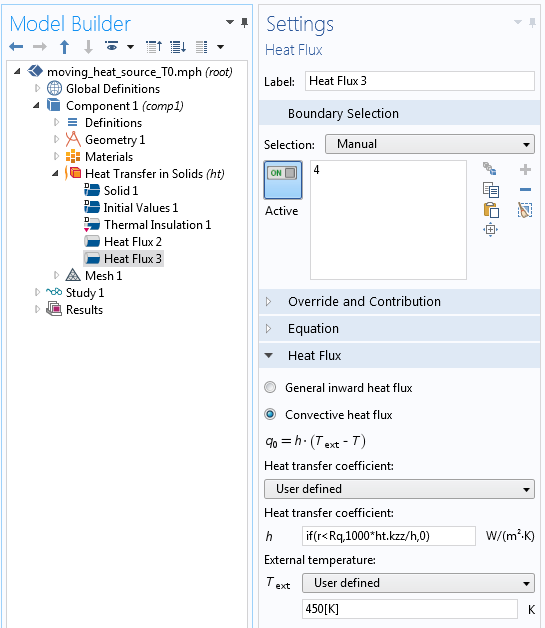
Das Festlegen der Temperatur mithilfe einer Konvektionsbedingung.
In den guten alten Zeiten, als ich begann die Finite-Elemente-Analyse zu nutzen, war es manchmal nicht möglich, in Finite-Elemente-Programmen für die Strukturmechanik Verschiebungen ungleich Null zu definieren. Diese Einschränkung wurde durch die zusätzliche Komplexität der Programmierung verursacht. In diesem Fall war die beste Option die Anwendung der Penalty-Methode durch Hinzufügen einer vorverformten steifen Feder. Allerdings sollte sie nicht zu steif sein; damals wurde noch mit einfacher Genauigkeit gerechnet!
Wenden wir uns nun der Neumann-Bedingung zu. Wir wollen einen Wärmestrom, der unabhängig von der Oberflächentemperatur ist. Im Falle des Wärmetransports besagt die Robin-Bedingung, dass der nach innen gerichtete Wärmestrom q
wobei \alpha der Wärmeübergangskoeffizient, T die Temperatur am Rand und T_{\textrm{ext}} die Außentemperatur ist.
Wenn also T_{\textrm{ext}} viel größer ist als die erwartete Temperatur an der Oberfläche, dann q \approx \alpha T_{\textrm{ext}}. Die Strategie besteht dann darin, einen beliebigen, sehr großen T_{\textrm{ext}} zu wählen und einen geeigneten Wärmeübergangskoeffizienten zu berechnen, wie im Folgenden gezeigt wird.
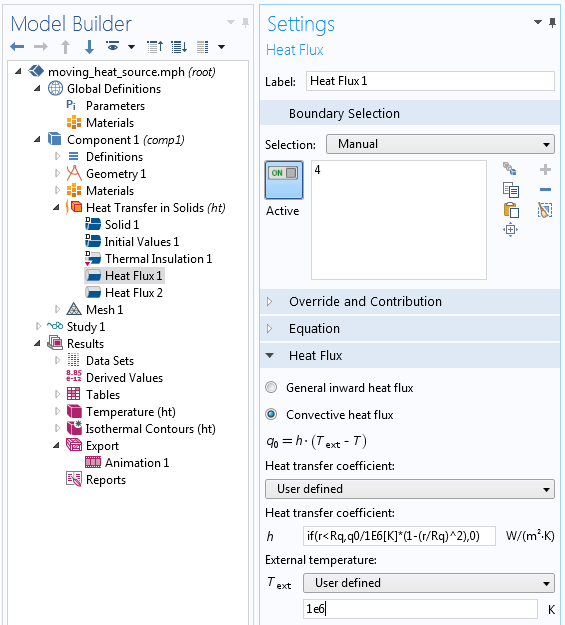
Verwendung einer Konvektionsbedingung zur Festlegung des Wärmestroms.
Konstrukteure nutzen dieses Prinzip, um eine feste Kraft in reale mechanische Komponenten einzubringen: eine vorgespannte lange schwache Feder. Wenn die Vorverformung der Feder viel größer ist als die Verschiebung der Teile, mit denen die Feder verbunden ist, ist die Kraft in der Feder nahezu konstant.
Der Umgang mit Diskretisierungsfehlern
Wenn eine Randbedingung durch einen booleschen Ausdruck wie if(r < R,... begrenzt wird, dann ist es mehr als wahrscheinlich, dass die Grenze des Bereichs, auf den sie angewendet wird, nicht den Kanten der Netzelemente folgt. Dies führt zu Diskretisierungsfehlern.
Für eine Neumann- oder eine Robin-Bedingung wird eine numerische Integration über jedes finite Element durchgeführt. Der Wert der Funktion wird an einer Anzahl von diskreten Gaußpunkten im Element ausgewertet. Wenn die Größe der Netzelemente im Vergleich zur geometrischen Größe der Last groß ist, dann kann die genaue Anzahl der von der Last abgedeckten Gaußpunkte die Gesamtlast erheblich beeinflussen. Daher sollten zu jedem Zeitpunkt mehrere Elemente auf der Fläche durch die Last abgedeckt sein.
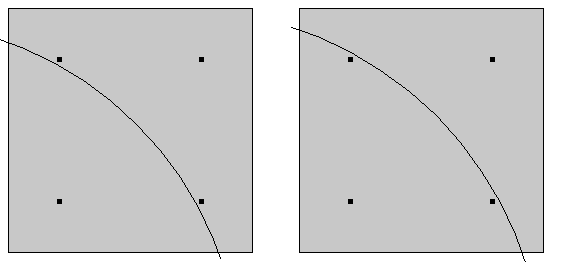
Eine kleine Änderung der Position der Last kann die Anzahl der Integrationspunkte verändern. (In Wirklichkeit ist die Anzahl der Integrationspunkte größer.)
Stattdessen werden Dirichlet-Bedingungen, zumindest im punktweisen Sinne, auf die Netzknoten angewendet. In der folgenden Abbildung sind die Temperaturverteilung und der Wärmestrom für eine bestimmte Zeit bei der Simulation des sich bewegenden kreisförmigen Punktes mit einer vorgegebenen Temperatur von 450 K dargestellt. Vor dem heißen Punkt ist ein dunklerer Schatten mit 260 K sichtbar. Da die Anfangs- und Umgebungstemperaturen in der Simulation 293 K betragen, ist dies nicht zu erwarten. Es handelt sich um einen numerischen Artefakt, der damit zusammenhängt, dass nicht alle Knoten auf jedem Element eine Dirichlet-Bedingung haben. Bei einer Diskontinuität der Dirichlet-Bedingungen kommt es zu Singularitäten. Dies wird in einem vorherigen Blog-Beitrag behandelt. Die Verfeinerung des Netzes wird diesen Effekt reduzieren.
Die grünen Pfeile in der folgenden Abbildung stellen die Knotenpunkte dar, an denen als Reaktion auf die Vorgabe der Temperatur ein Wärmezufluss entsteht. Bei der Netzdichte im Modell wird die Annäherung an einen Halbkreis eher grob sein.
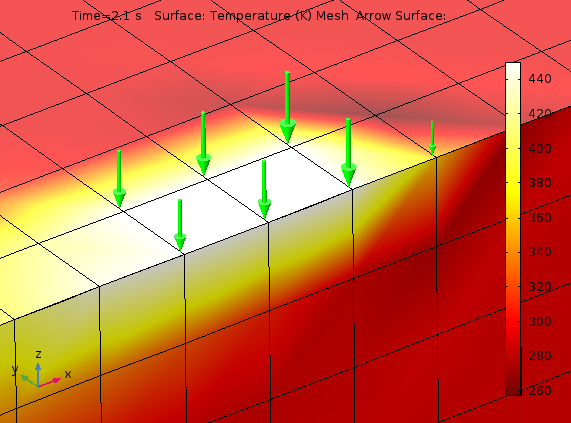
Temperaturverteilung und Wärmestrom um die halbkreisförmige vorgeschriebene Temperatur.
Lösungsabhängigkeit der Randbedingungen
Es gibt viele Möglichkeiten, wie die Lösung in Ihre Randbedingungen eingehen kann. Dadurch werden allgemein Nichtlinearitäten eingeführt, die von COMSOL Multiphysics® automatisch erkannt werden.
Betrachten wir als Beispiel einen Balken mit einer darunter liegenden Stütze, die ab einer bestimmten Biegung weitere Bewegung verhindert. Dies kann mit einer konditionalen Dirichlet-Bedingung über einen Prescribed Displacement/Rotation Knoten im Interface Beam implementiert werden.

Balken mit einer Biegung, Kontrollstütze und verteilter Last.
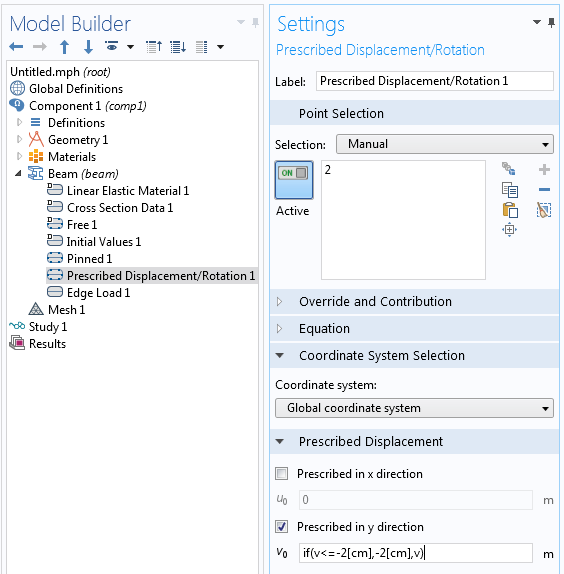
Einstellungen, die vorschreiben, dass der Balken bei einer Biegung von 2 cm anhalten soll.
Die Analyse zeigt das erwartete Verhalten. Bei niedrigeren Lasten ist die Form der Biegung symmetrisch, während sich bei höheren Lasten der Punkt auf dem Balken, an dem sich die zusätzliche Stütze befindet, nicht mehr bewegt. Bei der letzten Laststufe erfährt der Balken sogar einen Vorzeichenwechsel in der Krümmung. Dies ist im Verformungsdiagramm sichtbar, kann aber in einem Biegemomentdiagramm noch deutlicher dargestellt werden.
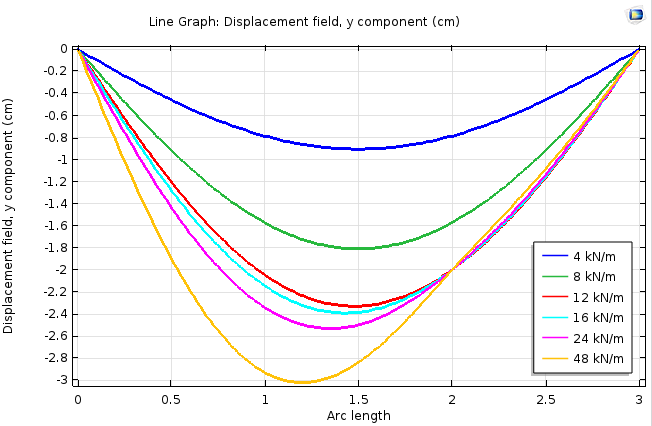
Die Balkenverschiebung am Stützpunkt stoppt bei 2 cm.
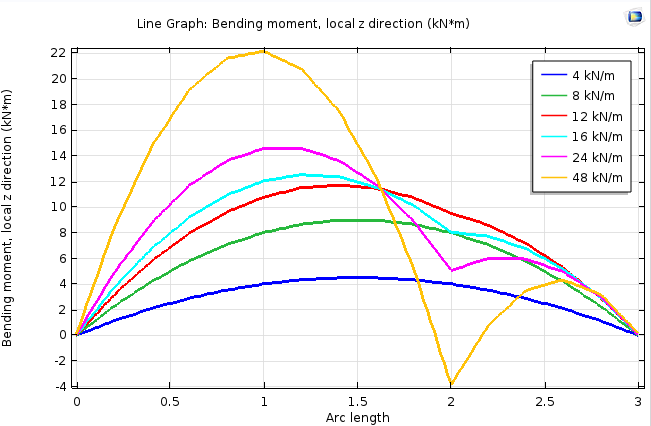
Biegemoment entlang des Balkens für verschiedene Laststufen.
Der hier vorgestellte Ansatz ist recht grob und die iterative Lösung hat möglicherweise keine guten Konvergenzeigenschaften. Eine stabilere Implementierung ist die Verwendung einer hochgradig nichtlinearen Feder am Stützpunkt, so dass die Reaktionskraft eine kontinuierlich differenzierbare Funktion der Verschiebung ist. Dies ähnelt der Art und Weise, wie der Penalty-Kontakt im Solid MechanicsInterface implementiert ist.
Abschließende Gedanken zur Nutzung von Randbedingungen in COMSOL Multiphysics®
COMSOL Multiphysics® ermöglicht Ihnen den Zugang zu sehr leistungsfähigen Mechanismen zur Festlegung von nicht standardisierten Randbedingungen. Wir haben Ihnen heute einige Beispiele dafür gegeben, was Sie mit diesen Bedingungen machen können.
Wenn Sie sich für die Analyse eines Modells mit einer sich bewegenden Last interessieren, werfen Sie einen Blick auf das Übungsmodell für eine sich bewegende Last, das Sie in unserer Anwendungsgalerie finden.
Wenn Sie weitere Fragen dazu haben, wie Sie nicht-standardisierte Randbedingungen in Ihren eigenen Modellierungsprozessen festlegen können, kontaktieren Sie uns noch heute.




Kommentare (0)