Statistik: Berechnung von Standardabweichungen und anderen statistischen Größen
Statistische Größen wie die Standardabweichung und der Mittelwert eines Datensatzes können wertvoll sein, wenn Sie die Leistung oder die Eigenschaften eines mit der Software COMSOL Multiphysics® simulierten Geräts, Systems oder Prozesses bewerten. In diesem Blog-Beitrag werfen wir einen Blick auf die Funktionen, Plots und andere Werkzeuge, die Ihnen in COMSOL Multiphysics® zur Berechnung und Visualisierung statistischer Größen zur Verfügung stehen.
Statistik: Ein Überblick
In der Statistik geht es um die Berechnung von Werten, die die Werte und Schwankungen von Daten darstellen oder visualisieren. In der folgenden Tabelle sind einige der gebräuchlichsten statistischen Maße mit den Namen der Operatoren und Datensatzoperationen in COMSOL Multiphysics® aufgeführt:
| Maß | Parameter | Name des Operators | Name der Datensatzoperation |
|---|---|---|---|
| Mittelwert oder Durchschnitt | \mu | mean, timeavg |
Average |
| Standardabweichung | \sigma | stddev |
Standard deviation |
| Varianz | Var, \sigma^2 | – | Variance |
Hier ein Überblick über jede dieser statistischen Maßnahmen:
- Der Mittelwert, Durchschnitt oder arithmetische Mittelwert (\mu in den folgenden Gleichungen) ist die Summe aller Datenwerte geteilt durch die Anzahl der Werte im Datensatz. Er ist ein nützlicher Wert zur Charakterisierung des Niveaus einer schwankenden Größe. Der Mittelwert kann empfindlich auf so genannte Ausreißer reagieren (d. h. auf Datenwerte, die erheblich von den anderen Werten im Datensatz abweichen). Eine verwandte statistische Größe ist der Median, der der mittlere Wert ist, der die obere Hälfte von der unteren Hälfte des Datensatzes trennt (oder der Mittelwert der beiden mittleren Werte, wenn der Datensatz eine gerade Anzahl von Werten enthält). Der Operator
timeavgin COMSOL Multiphysics® berechnet den Durchschnitt eines zeitabhängigen Ausdrucks über ein Zeitintervall. - Die Standardabweichung sigma in den folgenden Gleichungen) gibt an, wie stark die Daten vom tatsächlichen Mittelwert abweichen. Es ist die Quadratwurzel aus der Varianz. Im Gegensatz zur Varianz wird die Standardabweichung in denselben Einheiten ausgedrückt wie die Daten selbst.
- Die Varianz (Var in den folgenden Gleichungen) misst, wie weit ein Satz von Datenwerten von ihrem Mittelwert abweicht und wird in den Einheiten der Daten zum Quadrat ausgedrückt.
Die folgende Gleichung zeigt die Definition des Mittelwerts \mu:
Die nächste Gleichung definiert die Varianz:
wobei X die Variable ist, für die Sie die Varianz (und den Mittelwert) berechnen wollen, x_i die Menge der Werte, die sie annimmt, und \mu der Mittelwert. Diese Definition der Varianz gilt für eine feste Grundgesamtheit von Werten.
In COMSOL Multiphysics® stellen X und x_i eine feste Wertemenge dar.
Die Standardabweichung, \sigma, ist einfach die Quadratwurzel der Varianz:
Diese statistischen Formeln können leicht verallgemeinert werden, um statistische Größen zu beschreiben, die auf geometrischen Einheiten definiert sind, bei denen die Summation durch Integration ersetzt wird, was in COMSOL Multiphysics® der Fall ist. Die Integralform des Durchschnitts einer Variablen X über ein Gebiet Omega lautet
und, in ähnlicher Weise, die Varianz der Variable X über ein Gebiet Omega als
wobei |\Omega| die Größe des Gebiets ist (Volumen, Oberfläche oder Länge, je nach Raumdimension des Modells).
In den folgenden Abschnitten wird erläutert, wie diese Operationen und Operatoren in Simulationen mit COMSOL Multiphysics verwendet werden.
Statistische Größen in COMSOL Multiphysics®
Nichtlokale Kopplungsoperatoren
Später werden wir sehen, wie man den integrierten Operator stddev verwendet, um die Standardabweichung eines Ausdrucks zu berechnen. Zuvor betrachten wir die Auswertung des Durchschnitts einer berechneten Größe, etwa in einem Gebiet oder entlang von Rändern: Klicken Sie mit der rechten Maustaste auf den Knoten Definitions unter dem für Sie interessanten Knoten Component und wählen Sie dann Average aus dem Menü Nonlocal Couplings. Auf diese Weise wird ein Average Operator erstellt, standardmäßig aveop1, und in seinen Einstellungen definieren Sie zunächst das Geometric Entity Level (zum Beispiel Boundary) und dann die Ränder (oder andere geometrische Entitäten, je nach gewähltem Entity Level), für die Sie den Durchschnitt auswerten möchten. Auf die gleiche Weise können Sie auch Operatoren für die Berechnung von Integralen, Maximalwerten und Minimalwerten hinzufügen.
Sie können die von Ihnen erstellten Operatoren in einem Modell und beim Postprocessing verwenden. In einer Strömungssimulation können Sie zum Beispiel einen Durchschnittsoperator, der am Auslassrand definiert ist, zur Berechnung der durchschnittlichen Ausflussgeschwindigkeit verwenden. Fügen Sie dazu in einem Knoten Global Evaluation unter Derived Values im Abschnitt Results einen Ausdruck wie aveop1(spf.U) ein und klicken Sie dann auf Evaluate. Die durchschnittliche Geschwindigkeit für jede Ausgangszeit in einer transienten Simulation erscheint dann im Fenster Table.
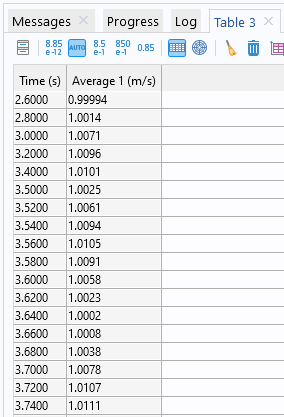
Ein Fenster Table mit den Werten der Durchschnittsgeschwindigkeit für jede Ausgabezeit.
Sie können eine Standardabweichung oder Varianz unter zweifacher Verwendung eines nichtlokalen Kopplungsoperators berechnen: einmal zur Berechnung des Durchschnitts und einmal zur Berechnung der Standardabweichung oder Varianz selbst. Wenn Sie etwa den Durchschnittsoperator aveop1 verwenden, der für den Auslassrand in unserem Beispiel der Strömung definiert ist, können Sie die Standardabweichung mit Global Evaluation und dem Ausdruck sqrt(aveop1((aveop1(p)-p)^2)) berechnen, wodurch die obigen Gleichungen für die Standardabweichung des Drucks am Rand implementiert werden.
Vereinfachen mit einem Ausdrucksoperator
Der obige Ausdruck sqrt(aveop1((aveop1(p)-p)^2)) ist etwas lang. Wenn Sie ihn an mehreren Stellen verwenden möchten, können Sie einen Expression Operator definieren, um ihn zu vereinfachen. Zuerst müssen Sie Variable Utilities unter dem Abschnitt General im Dialogfeld Show More Options aktivieren. Dann können Sie einen Expression Operator aus dem Untermenü Variable Utilities hinzufügen, das erscheint, wenn Sie mit der rechten Maustaste auf den Knoten Definitions unter Component klicken. In den Einstellungen des Knotens Expression Operator definieren Sie einen Operator, zum Beispiel stdop1, mit einem Ausdruck wie oben, aber mit einem Eingabe-Argument Ihrer Wahl, z. B. pin, wie in der folgenden Abbildung:
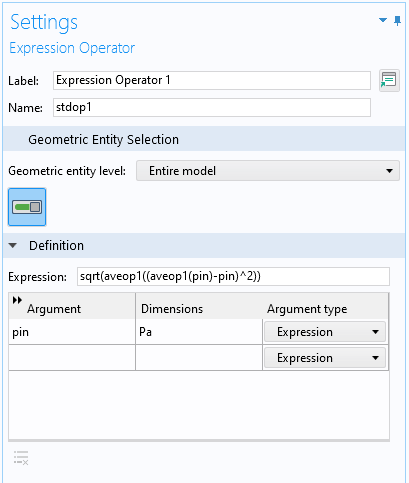
Das Einstellungsfenster für einen Expression Operator zur Definition eines vereinfachten Operators, stdop1, für die Standardabweichung.
Sie können diesen Operator dann beim Postprocessing verwenden, indem Sie stdop1(p) anstelle von sqrt(aveop1((aveop1(p)-p)^2)) eingeben.
Abgeleitete Werte
Für das Postprocessing können Sie die Knoten Volume Average, Surface Average und Line Average hinzufügen, die Sie implementieren, indem Sie mit der rechten Maustaste auf den Knoten Derived Values klicken und dann eine dieser Optionen aus dem Untermenü Average auswählen. Sie können ähnliche Knoten für die Werte Integration, Maximum und Minimum definieren.
Transformationen von Zeitreihen und parametrische Sweeps
Bei der Auswertung von Daten aus zeitabhängigen, parametrischen oder Eigenwertlösungen, etwa mit einem Feature Point Evaluation, können Sie eine der folgenden Operationen auf die Datenreihe anwenden:
- Durchschnitt
- Integral
- Maximum oder Minimum
- Quadratisches Mittel
- Standardabweichung
- Varianz
Jede dieser Operationen liefert eine einzelne Ausgabe, wobei es sich um den Durchschnitt eines Wertes in einem parametrischen Sweep oder um die Standardabweichung einer Größe an einem Punkt in einer zeitabhängigen Simulation handeln kann.
Integrierte Operatoren
Bei der Auswertung und dem Plotten der Ergebnisse einer Simulation in COMSOL Multiphysics haben Sie Zugriff auf eine große Anzahl von physikspezifischen Variablen sowie auf integrierte physikalische und mathematische Konstanten, Funktionen und Operatoren. Sie können diese direkt in ein beliebiges Feld Expression eingeben oder auf die Schaltfläche Add Expression oder Replace Expression klicken (verfügbar in der Symbolleiste des Abschnitts Expression in den Ergebnis-Features). Der folgende Screenshot zeigt die verfügbaren Operatoren in der Kategorie Integration and statistics ab COMSOL Multiphysics® Version 6.0:

Die verfügbaren Operatoren für Integration und Statistik.
Von besonderem Interesse ist der Operator stddev, mit dem Sie die Standardabweichung eines Ausdrucks berechnen können. Sie können ihn zur Berechnung der Standardabweichung für den gleichen Fall des Drucks am Auslassrand wie oben verwenden, indem Sie den Ausdruck stddev('comp1.aveop1',p) verwenden, was eine direktere und effizientere Syntax ist als der verschachtelte Aufruf des Durchschnittsoperators, der im vorherigen Ausdruck für die Standardabweichung verwendet wurde. Beachten Sie, dass die hier angegebenen Komponenten- und Operatornamen nur Beispiele sind und in Ihren Modellen andere Namen haben können.
Standardabweichung und Mittelwert: Ein Beispiel
Berechnen wir nun einige statistische Werte für das zeitabhängige Modell Strömung entlang eines Zylinders, das sich im Ordner Fluid Dynamics in der Application Library in COMSOL Multiphysics® befindet. Wir werden die folgenden Werte berechnen:
- Durchschnitt und Standardabweichung des Drucks im Rechengebiet für alle Zeitschritte der Simulation
- Durchschnitt und Standardabweichung der Geschwindigkeit an einem Punkt am Rande des Auslasses, berechnet über alle Zeitschritte
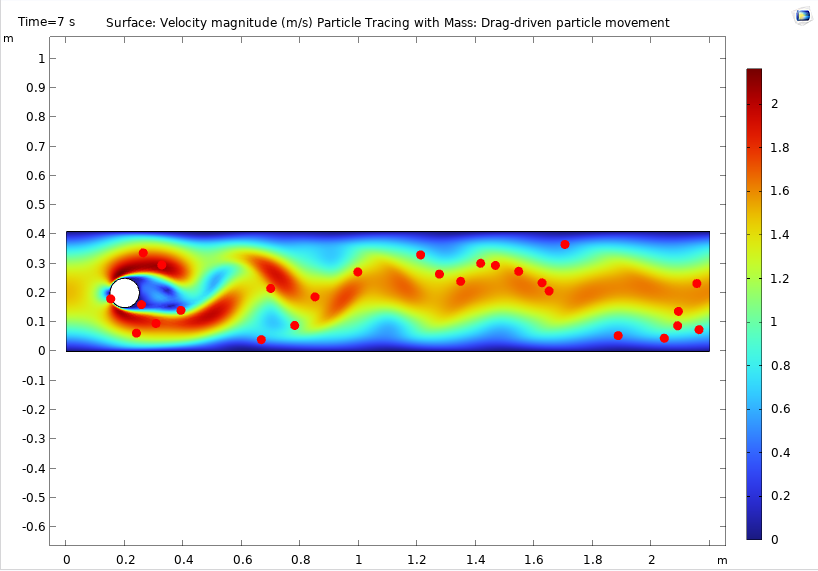
Der standardmäßige Plot für das Modell Flow Past a Cylinder, der das Geschwindigkeitsfeld und die Partikelbewegung am Ende der Simulation (7 s) zeigt.
Durchschnitt und Standardabweichung des Drucks im Gebiet und am Rand des Auslasses
Um den Durchschnitt und die Standardabweichung des Drucks im Gebiet zu ermitteln, fügen Sie zunächst einen Knoten Average für die nichtlokale Kopplung hinzu, sagen wir aveop2, und definieren ihn im Gebiet (es gibt nur ein Gebiet in dieser Geometrie). Nach der Berechnung der Lösung können Sie unter Derived Values im Abschnitt Results einen Knoten Global Evaluation hinzufügen, um den durchschnittlichen Druck mithilfe des Ausdrucks aveop2(p) auszuwerten. Der durchschnittliche Druck wird dann in einem Tabellenfenster für alle in der Liste Time selection ausgewählten Zeiten angezeigt. (Standardmäßig werden alle Zeitschritte berücksichtigt.) Wenn Sie den Durchschnitt des durchschnittlichen Drucks über alle Zeitschritte berechnen möchten, wählen Sie Average aus der Liste Transformation im Abschnitt Data Series Operation. Die Ausgabe ist dann eine einzelne skalare Zahl für den Durchschnitt des durchschnittlichen Drucks. Für die Standardabweichung bei jedem Zeitschritt verwenden Sie den Ausdruck stddev('comp1.aveop2',p) (oder eine der anderen genannten Optionen).
Das Argument für den Operator stddev muss nicht unbedingt ein Durchschnitt sein. Stattdessen können Sie ihm beispielsweise einen Integrationskopplungsoperator übergeben, und er würde immer noch eine korrekte Standardabweichung des Durchschnitts auswerten. Sie können ihn auch in Kombination mit dem Operator timeavg verwenden, um die gleichen Ergebnisse wie an anderen Stellen zu erhalten, indem Sie unter Verwendung eines Ausdrucks wie stddev('timeavg',t1,t2, expr) eine Datenoperation auf die Zeitreihe anwenden, wobei t1 und t2 die Start- bzw. Endzeiten für das Zeitintervall sind und expr der Ausdruck für die Berechnung des Zeitdurchschnitts über das Zeitintervall ist.
Um etwa die Standardabweichung des Drucks im Zeitbereich an jedem Punkt entlang des Auslassrands als Zeitmittelwert von 6 Sekunden bis 7 Sekunden darzustellen, verwenden Sie stddev('timeavg',6,7,p).
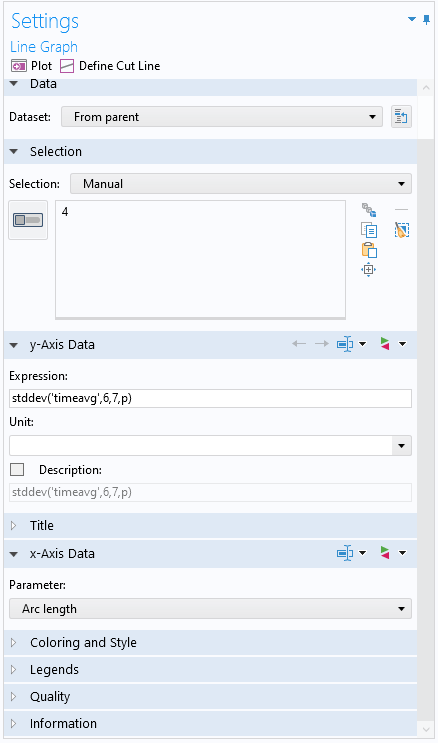
Das Einstellungsfenster für einen Plot eines Line Graph mit dem Ausdruck für eine Standardabweichung im Zeitbereich als Zeit-Durchschnittswert von 6 Sekunden bis 7 Sekunden.
Der entsprechende Plot zeigt, dass die Standardabweichung des Drucks in der Mitte des Auslassrands am geringsten ist.
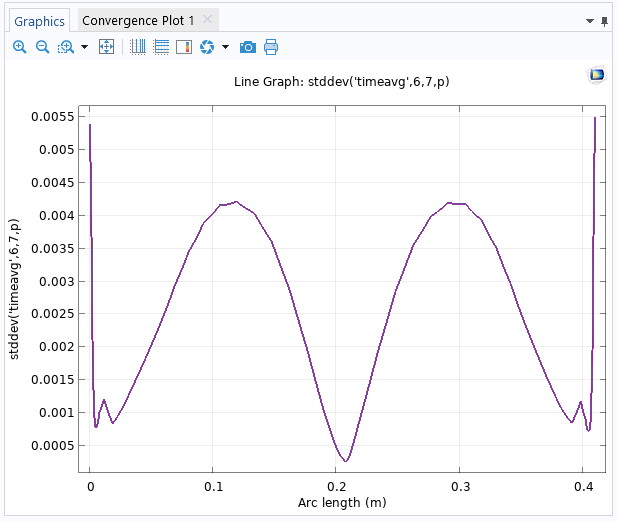
Der Plot des Line Graph der Standardabweichung im Zeitbereich am Auslassrand.
Durchschnitt und Standardabweichung der Geschwindigkeit am Auslass
Wenn Sie stattdessen den Durchschnitt und die Standardabweichung am Mittelpunkt des Auslassrandes über alle Zeitschritte auswerten wollen, müssen Sie zunächst die Geschwindigkeit an diesem Punkt ermitteln. Dies können Sie mit zwei Methoden tun:
- Hinzufügen eines Punktes in der Geometrie in der Mitte des Auslassrands, auch wenn er für die Erstellung der Geometrie nicht benötigt wird
- Hinzufügen eines Cut-Point-Datensatzes (in diesem Fall Cut Point 2D) und Definieren der Koordinaten für den Cut Point in den Einstellungen für den Datensatz
Um die Geschwindigkeit am Mittelpunkt auszuwerten, verwenden Sie einen Knoten Point Evaluation und wählen entweder den von Ihnen definierten Punkt aus oder verwenden den Datensatz Cut Point 2D als Eingabe-Datensatz (je nach der gewählten Methode für die Punktdaten). Verwenden Sie dann zum Beispiel spf.U als Ausdruck für den Geschwindigkeitsbetrag. Im Abschnitt Data Series Operation wählen Sie Average und dann Standard deviation. Klicken Sie nach jeder Auswahl auf Evaluate am oberen Rand des Einstellungsfensters, um den Mittelwert und die Standardabweichung (beide in m/s) für den Geschwindigkeitsbetrag in der Mitte des Auslasses über alle Zeitschritte der Simulation zu erhalten.

Der durchschnittliche Geschwindigkeitsbetrag und die Standardabweichung derselben Größe, die in einem Table angezeigt werden.
Histogramme
Histogramme sind nützlich, um die Form und Streuung bestimmter Daten zu veranschaulichen. Zu den Plot-Werkzeugen in COMSOL Multiphysics® gehören die folgenden Histogramm-Typen:
- Histogram (1D- und 2D-Plots), zeigt die Verteilung einer Größe über die Geometrie (d. h. das Netzvolumen). In 1D-Histogrammen stellt die x-Achse die Werte der Größe dar (als Anzahl von Klassen oder als Wertebereich), und die y-Achse stellt die Anzahl des gesamten Elementvolumens in jedem Intervall dar.
- Table Histogram (1D- und 2D-Plots), ähnelt einem Histogramm, basiert aber auf Daten aus einer Tabelle oder einer Evaluationsgruppe.
- Matrix Histogram (nur 2D Plots), können Sie verwenden, wenn Sie eine vorberechnete Matrix haben, die Sie als 2D-Histogramm visualisieren möchten.
Für die Plots Histogram und Table Histogram können Sie festlegen, ob Sie die Anzahl der Bins im Histogramm oder einen Bereich von Grenzwerten für die Bins angeben möchten. Für jedes 2D-Histogramm können Sie einen Unterknoten Height Expression hinzufügen, um die Größen der Bins entlang der z-Achse darzustellen, wie im folgenden 3D-Histogramm gezeigt.
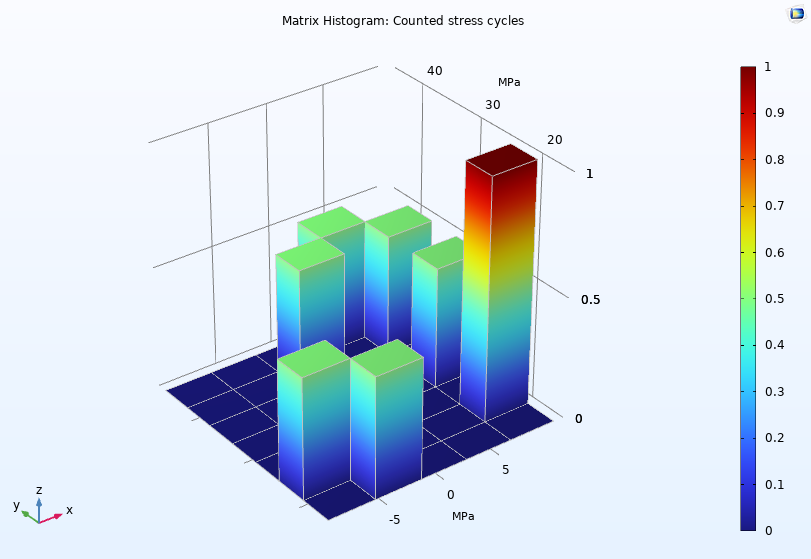
Der Plot eines Matrix-Histogramms visualisiert die gezählten Spannungszyklen im Modell Zykluszählung in der Ermüdungsanalyse – Benchmark.
Unsicherheitsquantifizierung und Statistik
Mit dem Uncertainty Quantification Module, einem Add-On zu COMSOL Multiphysics®, können Sie direkt in Ausgabetabellengruppen auf statistische Daten zugreifen, die sich auf Simulationen zur Unsicherheitsquantifizierung beziehen. Für eine Analyse der Fehlerfortpflanzung (Uncertainty Propagation) unter Verwendung von Ersatzmodellen mit nicht-adaptiven Gauß-Prozess werden beispielsweise die folgenden vier Tabellen verfügbar:
- Eine Tabelle QoI Confidence Interval, die eine Zeile pro Quantity of Interest (QoI) enthält, mit Spalten für den Mittelwert, die Standardabweichung, das Minimum und das Maximum, gefolgt von Konfidenzintervallen für 90%, 95% und 99% Wahrscheinlichkeit.
- Eine Tabelle UP Predicted QoI, die die vom Ersatzmodell vorhergesagten Werte für die QoI für die Monte-Carlo-Stichprobenpunkte enthält.
- Eine Tabelle UP Predicted Standard Deviation, die die vom Ersatzmodell vorhergesagte Standardabweichung für die Monte-Carlo-Stichprobenpunkte enthält. Dies kann als die eingebaute Fehlerschätzung des Ersatzmodells angesehen werden.
- Eine Tabelle Maximum Entropy, die die maximale relative Standardabweichung enthält, eine pro QoI.
Wenn ein Ersatzmodell mit adaptivem Gauß-Prozess verwendet wird, werden auch vier entsprechende adaptive Ergebnistabellen in die Gruppe der Ausgabetabellen aufgenommen. Sie enthalten die Ergebnisinformationen zu allen Anpassungsschritten.
Nächster Schritt
Als nächsten Schritt können Sie einige dieser statistischen Werkzeuge in Ihren eigenen Simulationsmodellen ausprobieren. Auf diese Weise können Sie ein statistisches Verständnis und eine Quantifizierung der Variationen und Eigenschaften von für Sie interessanten Variablen oder Parametern gewinnen. Wenn Sie Fragen zu diesem Thema haben, kontaktieren Sie COMSOL über die Schaltfläche unten.



Kommentare (0)