
In diesem Follow-up zu einem früheren Blogbeitrag über Dämpfung in der Strukturdynamik werfen wir einen detaillierten Blick auf die harmonische Antwort gedämpfter mechanischer Systeme. Darüber hinaus zeigen wir verschiedene Möglichkeiten, eine Frequenzantwortanalyse in der Software COMSOL Multiphysics® durchzuführen und die Ergebnisse zu interpretieren.
Was ist eine Frequenzantwort?
Im Allgemeinen zeigt die Frequenzantwort eines Systems, wie bestimmte Eigenschaften des Systems auf eine Eingabe als Funktion der Anregungsfrequenz reagieren. Wenn wir in COMSOL Multiphysics® von einer Frequenzantwort sprechen, meinen wir in der Regel die lineare (oder linearisierte) Antwort auf eine harmonische Anregung. Um eine Frequenzgangkurve zu erstellen, müssen wir einen Frequenz-Sweep durchführen, d.h. das Problem für eine Reihe verschiedener Frequenzen lösen. Eine Frequenzantwortkurve weist im Allgemeinen eine Reihe von deutlichen Spitzen auf, die bei den Eigenfrequenzen des Systems liegen.
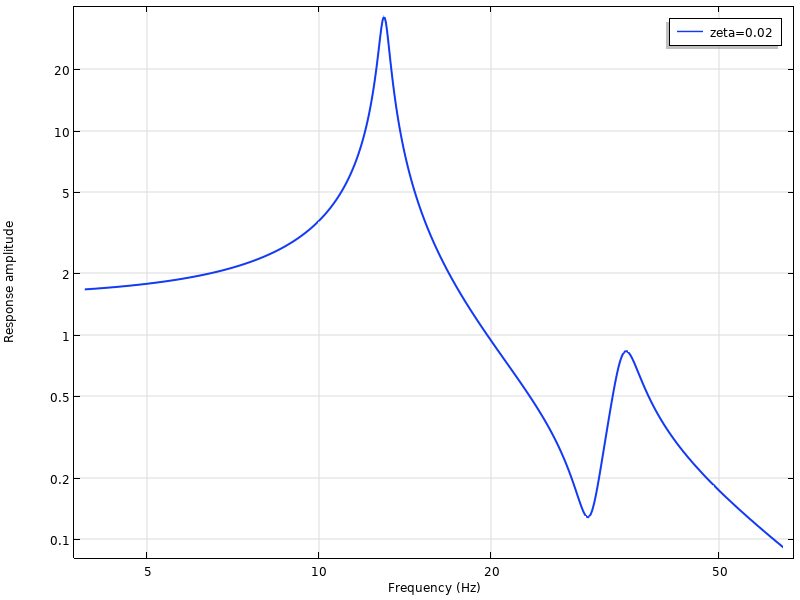
Eine typische Frequenzantwortkurve. Im aufgezeichneten Bereich gibt es zwei Eigenfrequenzen bei 13 Hz und 31 Hz.
Das Single-DOF-System, nochmals betrachtet
Im letzten Blogbeitrag wurden verschiedene Aspekte der Dynamik eines viskos gedämpften Single-DOF-Systems diskutiert. Daraus ergibt sich für die gedämpfte Eigenfrequenz:
\omega_d = \omega_0\sqrt{1-\zeta^2} \approx \omega_0 \left ( 1 – \frac{\zeta^2}{2} \right )
Dies ist die Frequenz, bei der das System (mit abnehmender Amplitude) schwingt, wenn es im verformten Zustand losgelassen wird und keine weitere äußere Anregung erfolgt.
Es stellt sich die interessante Frage: “Bei welcher Anregungsfrequenz ergibt sich die maximale Amplitude der Antwort?” Man würde erwarten, dass dies genau die gedämpfte Eigenfrequenz ist, aber wie wir weiter unten zeigen werden, ist dies nicht der Fall.
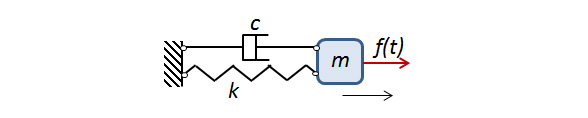
Ein Single-DOF-System.
Da es sich um eine harmonische Bewegung handelt, ist es sinnvoll, eine komplexe Notation zu verwenden, bei der der gemeinsame harmonische Multiplikator e^{i \omega t} ausfaktorisiert wird. Die Bewegungsgleichung lautet dann:
\left (-\omega^2m +ic\omega +k \right) u = f
Der Phasenwinkel der Last f kann als Referenz genommen werden, so dass f reellwertig ist. Eine normierte Form erhält man durch Division mit der Steifigkeit k:
\left (1-\left (\frac{\omega}{\omega_0} \right) ^2 +2i\zeta \left (\frac{\omega}{\omega_0} \right) \right) u = \frac{f}{k}
Die rechte Seite ist nun genau die statische Verschiebung. Das Verhältnis zwischen der dynamischen und der statischen Lösung ist also
\displaystyle H(\omega) = \left (1-\left (\frac{\omega}{\omega_0} \right) ^2 +2i\zeta \left (\frac{\omega}{\omega_0} \right) \right)^{-1} =\frac{1}{1-\beta ^2 +2i\zeta \beta}
Die Funktion H wird manchmal auch als Übertragungsfunktion bezeichnet.
Hier wird β verwendet, um das Verhältnis zwischen der Anregungsfrequenz und der ungedämpften Eigenfrequenz zu kennzeichnen. Der Betrag der Übertragungsfunktion ist
\displaystyle \left | \frac{1}{1-\beta ^2 +2i\zeta \beta} \right | = \frac{1}{\sqrt {(1-\beta ^2)^2 +4\zeta^2 \beta^2}}
Diese Funktion ist in der nachstehenden Grafik dargestellt.
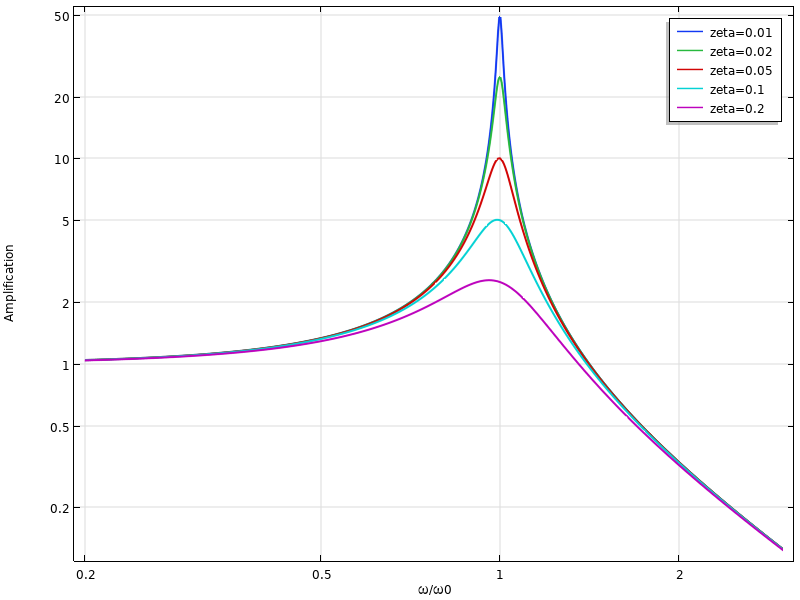
Mit Hilfe der Standardberechnung kann die Frequenz, die die maximale Amplitude ergibt, bestimmt werden, indem das Minimum des (quadrierten) Nenners {(1-\beta ^2)^2 +4\zeta^2 \beta^2} ermittelt wird. Das Ergebnis lautet
\beta = \sqrt{1-2 \zeta^2}
Die Anregungsfrequenz, die die maximale Antwort ergibt, ist also
\omega_{\mathrm {max}} = \omega_0\sqrt{1-2\zeta^2} \approx \omega_0 \left ( 1 – \zeta^2 \right )
und liegt unterhalb der gedämpften Eigenfrequenz. Tatsächlich ist die Frequenzverschiebung doppelt so groß.
Es mag paradox erscheinen, dass die Anregungsfrequenz, die zu einer maximalen Verstärkung führt, nicht mit der Frequenz der freien Schwingung übereinstimmt. Dies ist auf die durch die Dämpfung verursachte Phasenverschiebung zwischen Kraft und Lageänderung zurückzuführen. Ohne Dämpfung sind Kraft und Lageänderung unterhalb der Eigenfrequenz völlig gleichphasig, während sie oberhalb der Eigenfrequenz um 180° phasenverschoben sind. Mit Dämpfung ist der Übergang der Phasenverschiebung fließend, wie in der folgenden Grafik dargestellt. Unabhängig vom Dämpfungsgrad beträgt die Phasenverschiebung bei der ungedämpften Eigenfrequenz immer 90°.
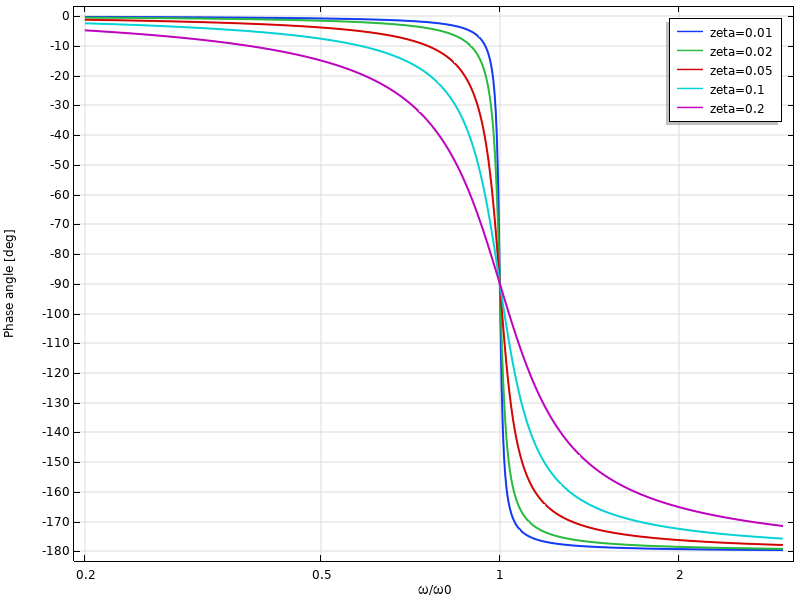
Phasenverschiebung der Auslenkung als Funktion der Frequenz.
Die Tatsache, dass Kraft und Verschiebung bei der Dämpfung leicht phasenverschoben sind, beeinträchtigt die Fähigkeit der Kraft, dem System Energie zuzuführen.
Verlustfaktordämpfung
Wiederholen wir die Analyse für ein Single-DOF-System mit Verlustfaktordämpfung. In diesem Fall lautet die Bewegungsgleichung
\left (-\omega^2m +k(1+i\eta ) \right) u = f
und die gedämpfte Eigenfrequenz kann wie folgt berechnet werden
\displaystyle \omega_d = \omega_0 \sqrt {\left( \frac{1}{2} \left( 1 + \sqrt{1+\eta^2} \right ) \right ) } \approx \omega_0 \left (1 + \frac{\eta^2}{8} \right )
Es mag überraschen, dass in diesem Fall die Dämpfung die Eigenfrequenz erhöht und nicht senkt. Die Erklärung dafür ist, dass diese Art der Darstellung der Verlustfaktordämpfung tatsächlich auch die Steifigkeit erhöht. Der Betrag der komplexwertigen Steifigkeit ist
|\tilde k| = k \sqrt {1 + \eta^2} \approx k \left ( 1+ \frac{\eta^2}{2} \right )
Mit dieser Verlustfaktordämpfung ist die Übertragungsfunktion
\displaystyle \frac{1}{1-\beta ^2 +i\eta }
und ihr Betrag ist
\displaystyle \left | \frac{1}{1-\beta ^2 +i\eta} \right | = \frac{1}{\sqrt {(1-\beta ^2)^2 +\eta^2}}
Man erkennt sofort, dass die maximale Amplitude bei β = 1 auftritt, also bei der ungedämpften Eigenfrequenz. Auch hier liegt das Verstärkungsmaximum bei einer Frequenz unterhalb der gedämpften Eigenfrequenz.
Die alternative Definition der Verlustfaktordämpfung, die im vorigen Blog-Beitrag erwähnt wurde, hat die Eigenschaft, dass der Absolutwert der komplexen Steifigkeit unabhängig vom Dämpfungsgrad ist. Dies wird durch die Verwendung einer Definition erreicht, die die komplexe Steifigkeit so normiert, dass sich eine reine Rotation in der komplexen Ebene ergibt,
\tilde k = \displaystyle \frac{k(1+i \eta)}{\sqrt{1+ \eta^2}}
Eine solche Formulierung führt zu einer Eigenfrequenz, die mit der Dämpfung abnimmt:
\displaystyle \omega_d = \omega_0 \sqrt { \frac {\frac{1}{2} \left( 1 + \sqrt{1+\eta^2} \right )}{1+ \eta^2} } \approx \omega_0 \left (1 – \frac{3\eta^2}{8} \right )
Eine Analyse, die hier nicht durchgeführt wird, wird eine entsprechende Verringerung der Anregungsfrequenz zeigen, die die maximale Verstärkung ergibt, so dass sie immer noch unter der gedämpften Eigenfrequenz liegt.
Besonders interessant ist die Phasenverschiebung zwischen Anregung und Antwort bei Verwendung der Verlustfaktordämpfung: Selbst bei sehr niedrigen Anregungsfrequenzen tritt noch eine Phasenverschiebung auf. Ihr asymptotischer Wert ist arctan(η).
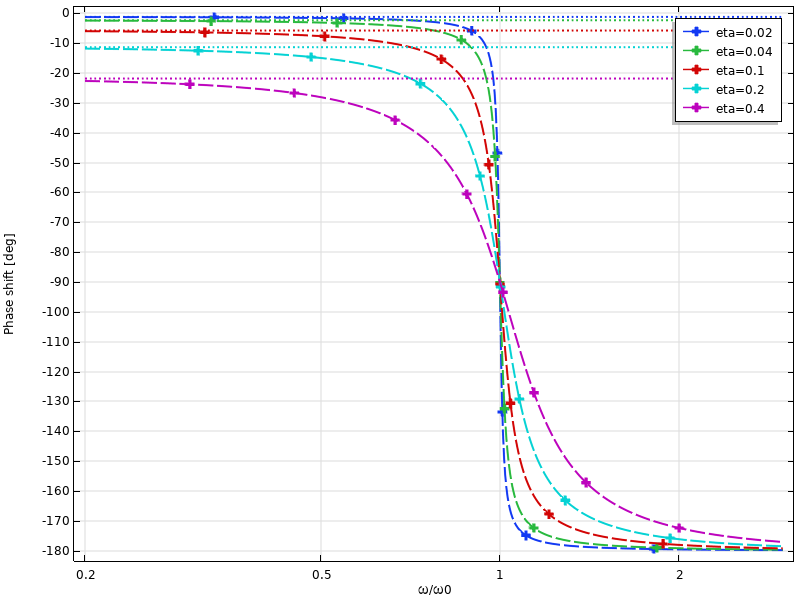
Phasenverschiebung der Auslenkung als Funktion der Frequenz bei Verwendung der Verlustfaktordämpfung. Die Asymptoten bei niedrigen Frequenzen sind durch die gestrichelten Linien gekennzeichnet.
Ein Wort zur Reibung
Wenn die Reibung zwischen zwei Oberflächen den Dämpfungsmechanismus darstellt, ist die Antwort auf eine harmonische Anregung aufgrund der Nichtlinearität des Systems nicht mehr harmonisch. Es kann immer noch eine periodische, aber unharmonische Antwort auftreten. Solche Aufgaben können nicht mit Frequenzbereichsmethoden gelöst werden, die von einer linearen Eingangs-Ausgangs-Beziehung ausgehen.
Modellierung der Frequenzantwort in COMSOL Multiphysics®
Aufbau der Studie
Nach dem Hinzufügen eines strukturmechanischen Physikinterafces im Modell Wizard wird Ihnen eine Reihe von Studientypen angezeigt, von denen vier für die Berechnung der Frequenzantwort verwendet werden können:
- Frequency Domain
- Frequency Domain, Prestressed
- Frequency Domain, Modal
- Frequency Domain, Prestressed, Modal

Verfügbare Studientypen für eine Solid Mechanics-Interface.
Zwei der Studien verwenden einen direkten Lösungsansatz und zwei den Modenüberlagerungsansatz. Bei den vorgespannten Analysetypen wird die Steifigkeitsänderung gegenüber einer stationären Vorspannung berücksichtigt. Die Modenüberlagerung eignet sich sehr gut für die Analyse im Frequenzbereich, da es einfach ist, die geeigneten Eigenformen auf der Basis der gegebenen Frequenzen auszuwählen.
In beiden Fällen kann ein Frequenzsweep durchgeführt werden, indem in den Studieneinstellungen eine Liste von Frequenzen angegeben wird, für die die Antwort berechnet wird. Häufig ist es wünschenswert, die Frequenzen um die Eigenfrequenzen der Struktur zu gruppieren.
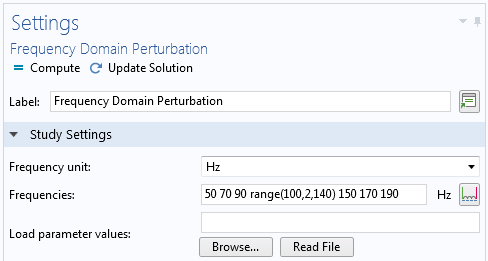
Eingabe der Frequenzen für einen Frequenzsweep.
Es ist zu beachten, dass ohne Dämpfung der Frequenzgang genau bei einer Eigenfrequenz gegen unendlich geht. Das bedeutet, dass es nicht möglich ist, eine ungedämpfte Frequenzgangaufgabe bei oder in der Nähe einer Eigenfrequenz zu lösen. Die numerische Formulierung wird eine singuläre oder zumindest schlecht konditionierte Systemmatrix ergeben.
Perturbation oder nicht?
Es gibt eine sehr wichtige Einstellung im Stationary-Knoten der Lösersequenz für eine Studie im Frequenzbereich: Linearity.
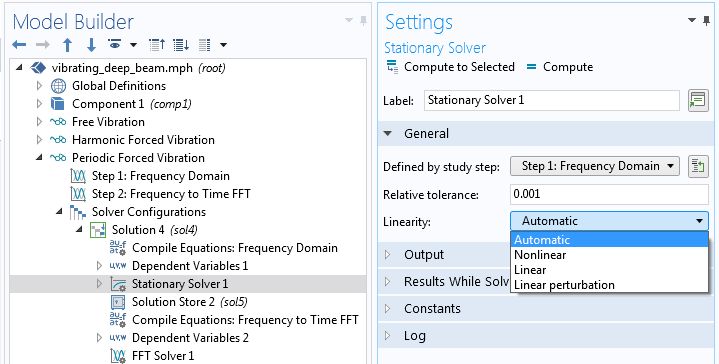
Auswahl des Linearity -Features.
Im Prinzip kann jede Analyse im Frequenzbereich als kleine Störung betrachtet werden, so dass die Verwendung der linearen Störung (Linear perturbation) nie falsch ist. Der häufigste Fall ist jedoch, dass die Schwingungen um den Nullpunkt zentriert sind. In diesem Fall spielt es keine Rolle, ob das Problem als linear (Linear) oder als lineare Störung (Linear Perturbation) betrachtet wird. Die Umgebung ändert jedoch immer grundlegend die Interpretation von Lasten. Eine Last kann als harmonische Störung (Harmonic Perturbation) charakterisiert werden. Eine solche Last wird nur berücksichtigt, wenn Linearity auf Linear perturbation gesetzt ist. Alle Lasten, die nicht als Harmonic Perturbation gekennzeichnet sind, werden in einer solchen Studie ignoriert. Umgekehrt werden alle als Harmonic Perturbation gekennzeichneten Lasten ignoriert, wenn Linearity nicht auf Linear perturbation eingestellt ist, und andere Lasten werden als harmonisch betrachtet.

Eine Kantenbelastung, bezeichnet als Harmonic Perturbation.
Der Zweck dieser Einstellung ist es, zwischen den Lasten, die einen möglichen Vorspannungszustand verursachen, und der zusätzlich wirkenden harmonischen Anregung unterscheiden zu können.
Wenn eine Frequenzbereichsstudie (Frequency Domain) hinzugefügt wird, ist diese standardmäßig nicht als Störung eingestellt. Daher sollte das Tag Harmonic Perturbation in diesem Fall nicht für Lasten verwendet werden, es sei denn, die Einstellung Linearity wird geändert. Durch Hinzufügen einer Studie Frequenzbereich, vorgespannt (Frequency Domain, Prestressed) wird der Frequenzbereichsstudienschritt für die Störungsanalyse eingerichtet. Handelt es sich um eine Studie vom Typ Modenüberlagerung, ist die Studie immer vom Typ lineare Störung.
Interpretation der Ergebnisse
Die Ergebnisse einer Analyse im Frequenzbereich sind komplexwertig, und die harmonische Variation ist implizit. Der Phasenwinkel der komplexen Zahl beschreibt die Phasenverschiebung gegenüber der Referenzphase (die willkürlich gewählt werden kann, aber oft als Phase der Hauptlast betrachtet wird). Er gibt auch Auskunft über die Phasenverschiebung zwischen verschiedenen Punkten in der Struktur. Da die Verschiebungskomponenten innerhalb eines einzelnen finiten Elements unterschiedliche Phasenwinkel haben können, ist es durchaus möglich, dass die Komponenten des Spannungstensors nicht in Phase zueinander sind. Dies kann z. B. bei der Ermüdungsanalyse von Bedeutung sein.
In vielen Fällen, z. B. bei einer Farbdarstellung, ist es nur möglich, eine reelle Zahl anzuzeigen. Für die Darstellung aller Ergebnisse gilt folgende Konvention: Wird eine komplexwertige Variable v in einem Kontext abgefragt, in dem ein reeller Wert erwartet wird, so wird der reelle Anteil verwendet.
\displaystyle v = \Re(\tilde v e^{i \phi})
Der Phasenwinkel Φ ist eine Eigenschaft des Datensatzes, die verändert werden kann.
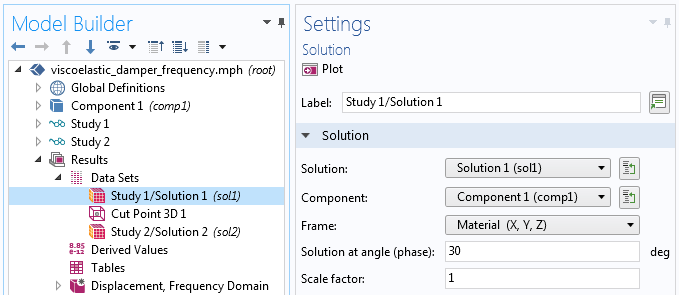
Anpassen des Phasenwinkels im Datensatz.
Bei den meisten Frequenzganganalysen ist man an der Amplitude einer Ergebnisgröße, v, als Funktion der Frequenz interessiert. Das bedeutet, dass abs(v) und nicht v selbst untersuchen werden muss. Der Unterschied zwischen den beiden ist in der folgenden Abbildung dargestellt.
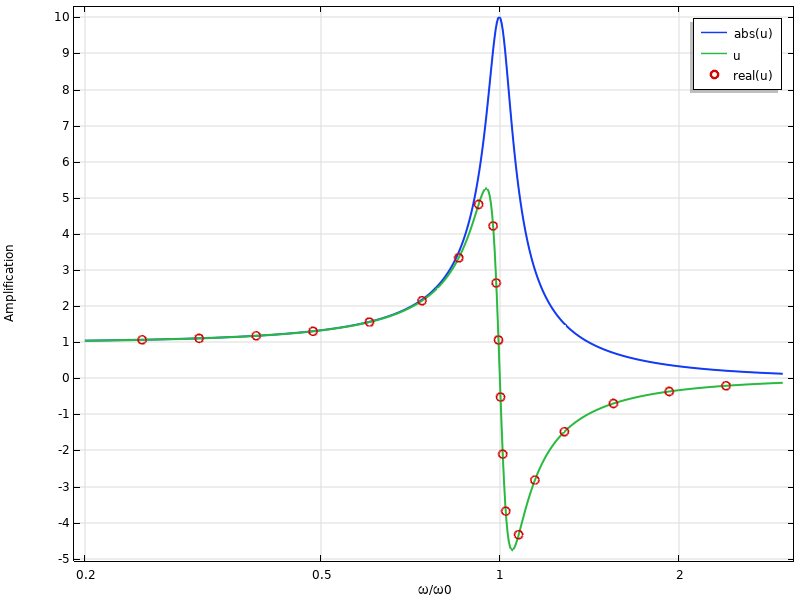
Beispiel für ein Frequenzantwortdiagramm. Beachten Sie, dass der Graph von “u” identisch mit “real(u)” ist.
Um zu sehen, was im Einzelnen passiert, können wir den Imaginärteil und das Argument der Ergebnisgröße in den Graphen eintragen:
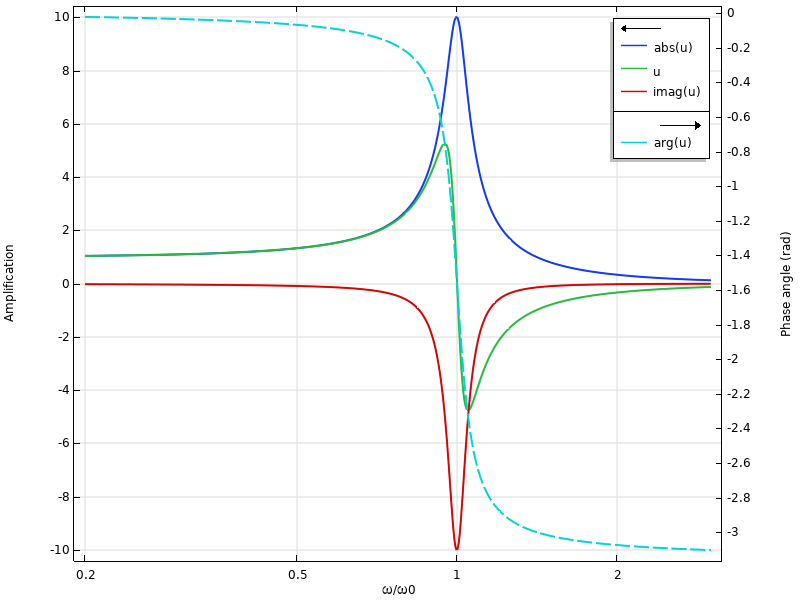
Frequenzantwort einschließlich Phasenverschiebung.
Bei tiefen Frequenzen liegt der Realteil nahe am Absolutwert. In der Nähe der Eigenfrequenz dominiert dagegen der Imaginärteil. Das bedeutet, dass die Antwort nahezu phasenverschoben zur Anregung ist.
Betrachten wir nun, was passiert, wenn wir den Phasenwinkel im Datensatz auf 45° ändern.
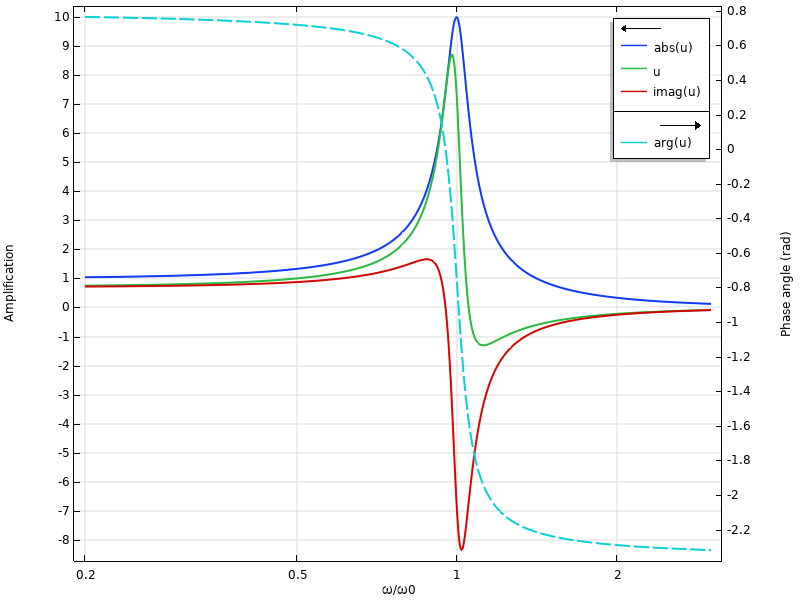
Frequenzantwort für einen Phasenwinkel im Datensatz von 45°.
Die Amplitudenkurve ändert sich erwartungsgemäß nicht. Die einzelnen Werte des Real- und Imaginärteils ändern sich jedoch. Die Phasenwinkelkurve verschiebt sich um π/4 nach oben. Dies ist genau die gleiche Kurve, die wir erhalten würden, wenn wir der Last einen Phasenwinkel von 45° hinzufügen würden.
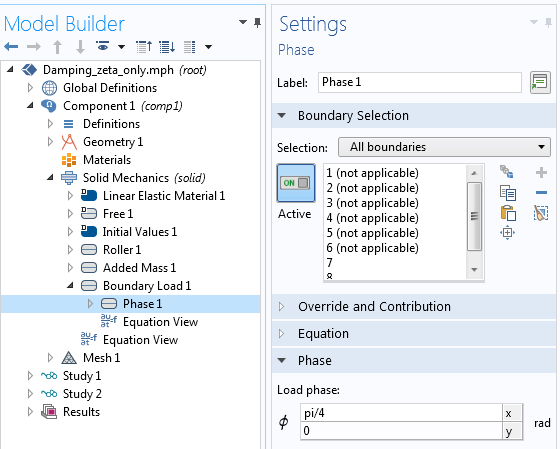
Hinzufügen eines Phasenwinkels zu einer Last.
Anstelle der Eingabe des Phasenwinkels kann die Last auch direkt in komplexer Notation eingegeben werden:
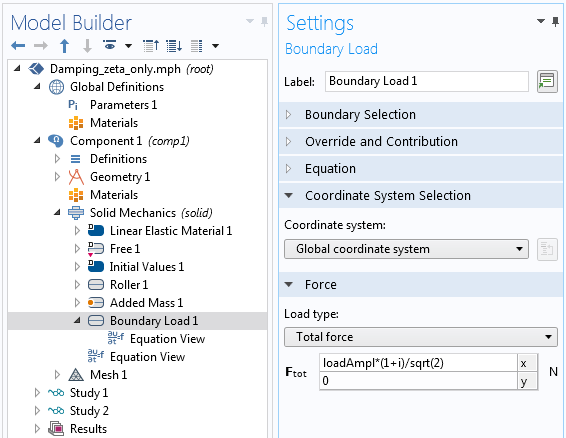
Komplexe Darstellung der gleichen Last wie oben.
Die Möglichkeit, den Phasenwinkel vorzugeben, ist wichtig, wenn nicht alle Lasten zueinander in Phase sind. Eine rotierende Unwuchtmasse kann z.B. gut beschrieben werden, indem die Last in Richtung y gegenüber der Last in Richtung x um 90° phasenverschoben wird.
Ergebnisse einer Störungsanalyse
Bei einer Störungsanalyse gibt es zwei Ergebnissätze: die Vorspannungslösung und die Störungslösung. In diesem Fall haben Sie Zugriff auf eine zusätzliche Auswahl in den verschiedenen Funktionen zur Ergebnisdarstellung: Expression evaluated for.
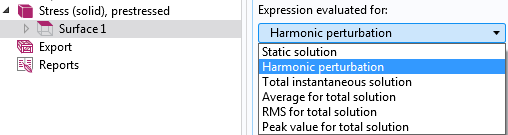
Auswahl der Auswertungsart für eine Perturbationsanalyse.
Hier können Sie wählen, ob Sie die Störungslösung, die Vorspannungslösung oder eine Kombination aus beiden untersuchen wollen. Für die Störungslösung gibt es eine weitere Option: das Kontrollkästchen Compute differential.

Auswahl Compute differential.
Diese Einstellung beeinflusst die Behandlung von nichtlinearen Ausdrücken. Wenn die Option Compute differential nicht ausgewählt ist, wird eine nichtlineare Größe als nominal angenommen. Beispielsweise wird für den Ausdruck u^2 einfach das Quadrat der Variablen u aus der Störungslösung genommen. Da u im Allgemeinen komplexwertig ist, ist dies normalerweise eine unsinnige Operation.
Wird die Option Compute differential gewählt, so wird die nichtlineare Größe um den vorgespannten Zustand linearisiert. Der Ausdruck u^2 wird in 2*u0*u umgewandelt, wobei u0 der Wert am Linearisierungspunkt ist.
Umwandlung von Frequenzgangmessungen in den Zeitbereich
Es gibt Situationen, in denen man die harmonische Antwort einer Frequenzbereichsanalyse im Zeitbereich visualisieren möchte. Dies ist insbesondere dann der Fall, wenn mehrere Anregungsfrequenzen vorliegen.
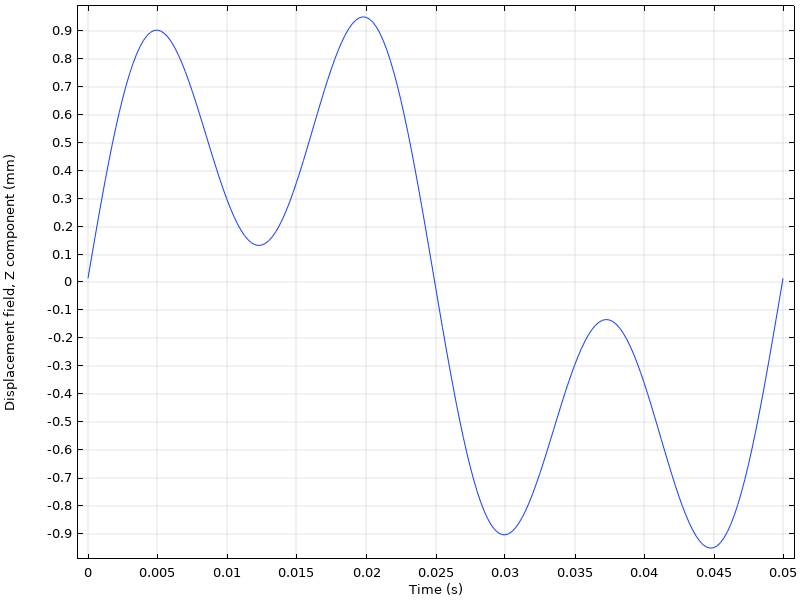
Antwort auf die Anregung von zwei Lasten mit unterschiedlichen Frequenzen.
Die Ergebnisse aus dem Frequenzbereich können in den Zeitbereich transformiert werden, indem der Studienschritt Frequency to Time FFT verwendet wird.

Studiensequenz zur Umwandlung von Ergebnissen aus dem Frequenzbereich in den Zeitbereich.
Diese Technik wird in den folgenden Tutorialmodellen verwendet:
Abschließende Bemerkungen
Die Frequenzbereichsanalyse ist ein leistungsfähiges Werkzeug zur Analyse linearer Systeme, die einer harmonischen Erregung ausgesetzt sind. Durch die Durchführung einer Fourier-Transformation der Belastung kann jede Art von periodischer Anregung mit Hilfe der Frequenzganganalyse untersucht werden.
In der Anwendungsgalerie finden Sie viele weitere Beispiele für mechanische Frequenzganganalysen, wie z.B:




Kommentare (0)