Berechnung von Verlust, Temperatur und Wirkungsgrad in Elektromotoren

Wir haben bereits die Analyse von Elektromotor- und Generatordesigns in der Software COMSOL Multiphysics^®, einschließlich der Untersuchung der Verteilung des magnetischen Flusses, des Drehmoments, der Verluste und des Eisenverbrauchs in einer rotierenden Maschine, behandelt. Als Beispiel haben wir eine 12-nutige, 10-polige Permanentmagnetmaschine (PMM) mit einem Durchmesser von 35 mm und einer axialen Länge von 80 mm verwendet. In diesem Blog-Beitrag untersuchen wir die Variation der Eisen- und Kupferverluste, den daraus resultierenden Temperaturanstieg und die Auswirkungen auf den Wirkungsgrad der PMM. Da wir uns mit Verlusten befassen, wollen wir zunächst einen Blick auf einen sehr grundlegenden Aspekt der Simulation rotierender Maschinen werfen: die Energieerhaltung.

Dies ist der zweite Blog-Beitrag einer Reihe, die sich mit der Analyse verschiedener Konstruktionsaspekte von rotierenden Maschinen mit COMSOL Multiphysics^® befasst. Lesen Sie Teil 1 hier.

Überprüfung der Leistungsbilanz

Die Energieerhaltung kann durch eine Überprüfung der relevanten Leistungswerte untersucht werden. Zu diesem Zweck werden wir das Phänomen der Leistungsbilanz im Zusammenhang mit der Simulation rotierender Maschinen betrachten. Bei der Modellierung rotierender Maschinen wird dem Stator- und Rotoreisen in der Regel eine elektrische Leitfähigkeit von Null zugewiesen und die Eisenverluste werden mit empirischen Modellen wie Steinmetz oder Bertotti separat berechnet. Dies liegt daran, dass die Stator- und Rotoreisen aus Blechpaketen bestehen, um die Wirbelströme zu minimieren.

Würde man die Gesamtleitfähigkeit von Eisen verwenden, würde das numerische Modell die Verluste stark überschätzen und ein niedriges Nettomagnetfeld berechnen, was nicht-laminiertem Eisen entspricht. Aus diesem Grund müssen die Eisenverluste separat berechnet werden. Mit diesem Ansatz kann der Wirkungsgrad berechnet werden als \textrm{Wirkungsgrad} = \frac{\textrm{Mechanische Ausgangsleistung}}{\textrm{Mechanische Ausgangsleistung + Eisenverluste + Kupferverluste}}. Hier haben wir uns entschieden, die Reibungs- und Lüftungsverluste zu vernachlässigen, da wir wissen, dass sie mit etwa 3% nur einen kleinen Teil des Gesamtverlustes ausmachen. Wenn es notwendig sein sollte, können diese Terme leicht einbezogen werden.

Aus den bisherigen Erkenntnissen ergibt sich, dass bei elektromagnetischen FEM-Simulationen die elektrische Eingangsleistung zur Anregung der Magnetfelder und zur Erzeugung des Drehmoments am Rotor und der Kupferverluste verwendet werden sollte. Hinsichtlich der Energieerhaltung sollte die elektrische Eingangsenergie der Summe der mechanischen Ausgangsleistung und der Kupferverluste entsprechen. Die momentane elektrische Leistung ist gegeben durch P_i = V_a I_a + V_b I_b + V_c I_c, wobei V_a, V_b, V_c und I_a, I_b, I_c die dreiphasigen Spannungen bzw. Ströme des Stators sind. Die mechanische Ausgangsleistung ist gegeben durch P_o = T_r \omega_r, wobei T_r das Drehmoment am Rotor und \omega_r die Winkelgeschwindigkeit ist.

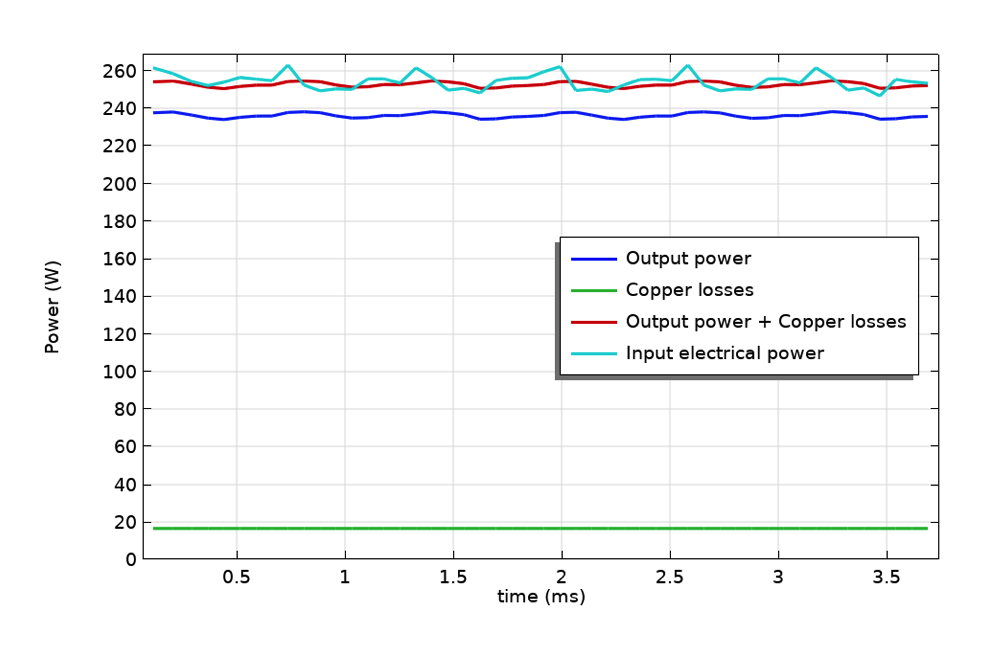
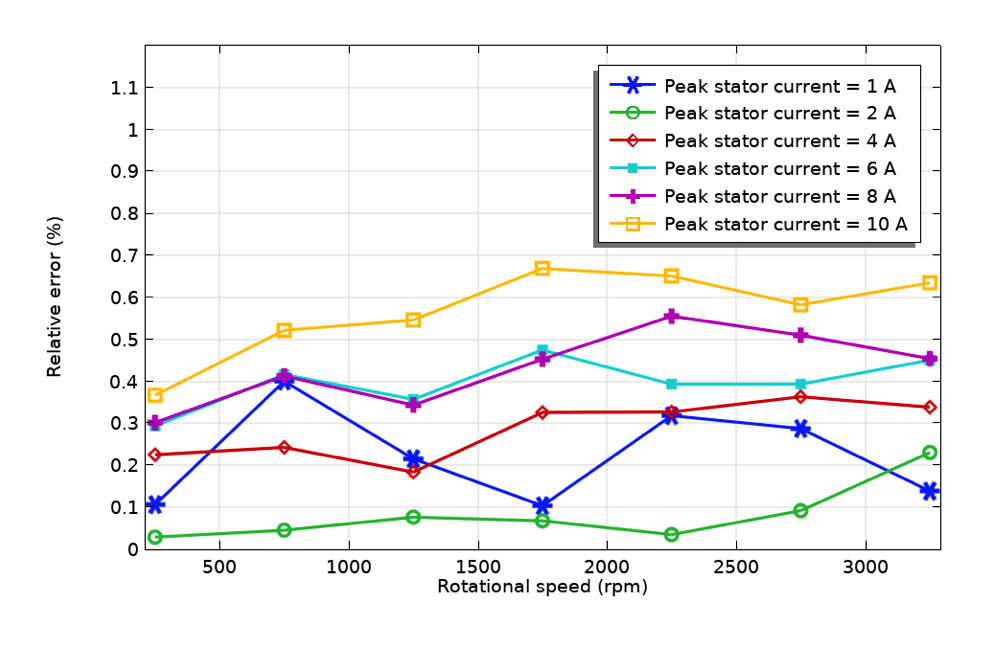
Links: Die momentane Leistungsbilanz bei einer Rotordrehzahl von 3250 U/min und einem Statorstrom von 10 A. Rechts: Gemittelte Leistungsbilanz (der relative Fehler zwischen Eingangsleistung und der Summe aus Ausgangsleistung und Kupferverlusten).

Die momentane Leistungsbilanz kann untersucht werden, indem man die zeitliche Entwicklung der mechanischen Ausgangsleistung, der Kupferverluste, ihrer Summe und der elektrischen Eingangsleistung beobachtet. Zur weiteren Untersuchung der Leistungsbilanz werden der zeitliche Mittelwert der elektrischen Eingangsleistung und die Summe aus Ausgangsleistung und Kupferverlusten für verschiedene Kombinationen von Rotordrehzahl und Statorstrom ermittelt. Der relative Fehler zwischen der Eingangsleistung und der Ausgangsleistung plus Verluste wird berechnet. Über den gesamten Variationsbereich beträgt der maximale relative Fehler weniger als 1 %. Die Überprüfung der Leistungsbilanz stellt sicher, dass keine unbeabsichtigten Verluste vorhanden sind, und bestätigt uns darin, die numerische Analyse als Instrument für die Entwicklung rotierender Maschinen einzusetzen.

Untersuchung von Eisen- und Kupferverlusten

Die Berechnung der Verluste ist aufgrund ihrer Bedeutung für die Berechnung des Wirkungsgrades und die Bewertung des Temperaturanstiegs wichtig. Die Eisenverluste bestehen aufgrund einer zeitlich veränderlichen magnetischen Flussdichte aus Hysterese- und Wirbelstromverlusten im Rotor- und Statoreisen. Bei den Kupferverlusten handelt es sich um die ohmschen Verluste, die wegen des Leitstromflusses in den Statorspulen auftreten.

Mit dem Feature Parametric Sweep können wir die Variation der Eisen- und Kupferverluste mit der Rotordrehzahl und dem Statorstrom untersuchen. Die Verluste können mit der seit COMSOL Multiphysics^® Version 5.6 verfügbaren Unterfunktion Loss Calculation berechnet werden. Für das laminierte Eisen werden die empirischen Modelle von Steinmetz und Bertotti verwendet, die uns den Gesamtverlust aufgrund von Hysterese und Wirbelströmen liefern. Das Bertotti-Verlustmodell ermöglicht es dem Nutzer, den Wert der Laminatdicke anzugeben. Ein vollständig benutzerdefiniertes Materialmodell mit einer eigenen angepassten B-H-Kurve steht ebenfalls zur Verfügung. Anspruchsvollere Effekte, wie Anisotropie, können ebenso in die Simulation einbezogen werden. Die Kupferverluste werden mit der Option Resistive losses, die auf dem Ohmschen Gesetz basiert, in der Unterfunktion Loss Calculation ermittelt.

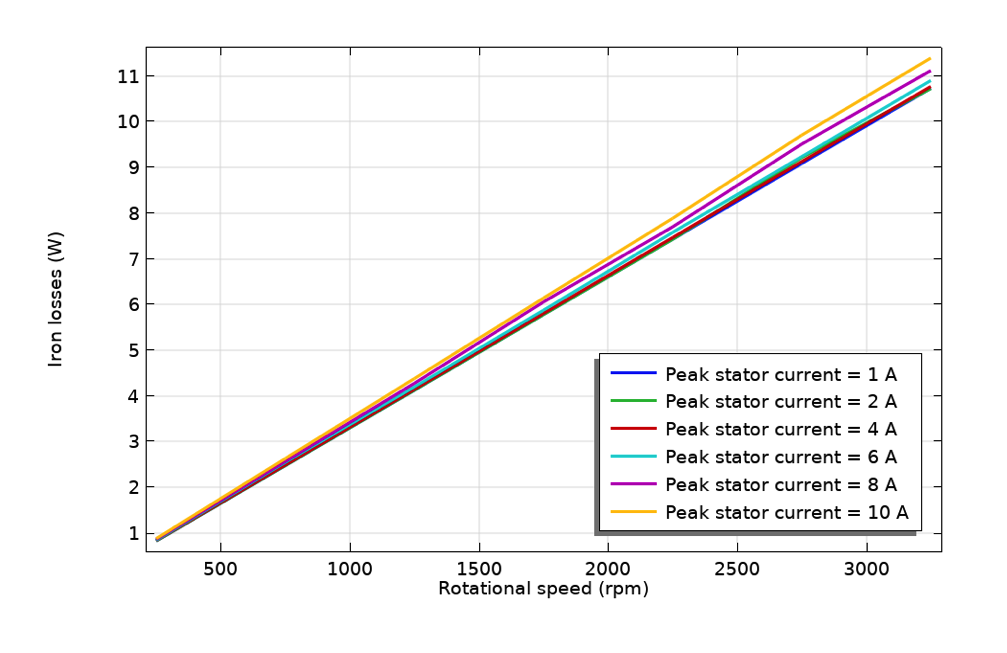
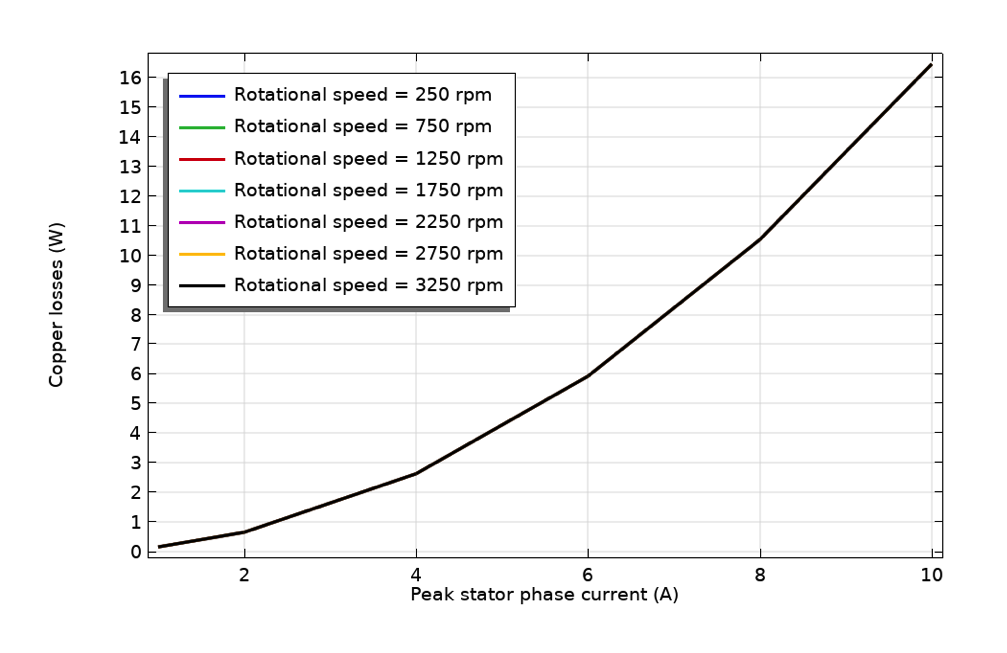
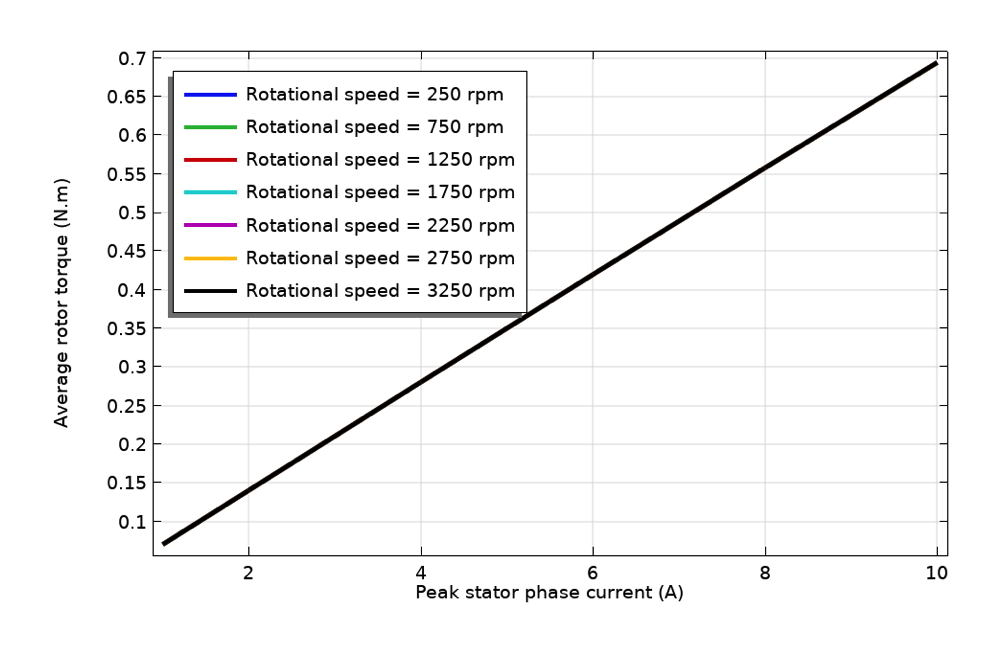
Variation des Eisenverlusts mit der Rotordrehzahl (links), des Kupferverlusts mit dem Statorstrom (Mitte) und des Rotordrehmoments mit dem Statorstrom (rechts).

Eisenverluste

Die Eisenverluste variieren linear mit der Rotordrehzahl und hängen nicht stark vom Statorstrom ab. Das lässt sich durch Korrelation mit empirischen Verlustmodellen nachvollziehen. Eisenverluste können mit der Steinmetz-Gleichung berechnet werden, die durch W_i = K_h{B_m}^\alpha f gegeben ist, wobei W_i der Eisenverlust pro Volumeneinheit, B_m die maximale magnetische Flussdichte und f die Frequenz der Variation der magnetischen Flussdichte ist.

Dieser Ausdruck legt nahe, dass die Eisenverluste linear mit der Frequenz variieren, die wiederum direkt proportional zur Rotordrehzahl ist. Außerdem wird die magnetische Flussdichte im Eisen in erster Linie von den Magneten bestimmt. Der Statorstrom hat nur einen marginalen Einfluss. Infolgedessen skaliert der Eisenverlust linear mit der Rotordrehzahl und hängt kaum vom Statorstrom ab.

Kupferverluste

Die Kupferverluste hingegen variieren quadratisch mit dem Statorstrom. Diese quadratische Variation lässt sich leicht verstehen, wenn man die Formel für ohmsche Verluste betrachtet, die durch W_c = I^2 R_c gegeben ist, wobei I der Spulenstrom und R_c der Spulenwiderstand ist. Da in diesem Fall das Feature Homogenized Multiturn Coil verwendet wird, werden Skin-Effekte und Proximity-Effekte in der Spule vernachlässigt – eine Annahme, die gilt, wenn die Drähte in Bezug auf die Skin-Tiefe dünn sind – und so hängt der effektive R_c nicht von der Rotordrehzahl ab.

Rotordrehmoment

Wir können auch die Variation des Rotordrehmoments mit dem Statorstrom untersuchen, um die Drehmomentkonstante für das gegebene Motordesign zu ermitteln. Das Drehmoment ist proportional zum Statorstrom und relativ unabhängig von der Drehzahl. Das Drehmoment wird durch die Wechselwirkung zwischen dem Statorstrom und dem Magnetfeld des Rotors erzeugt. Bei einem PMM wird das Magnetfeld des Rotors durch Permanentmagnete erzeugt. Bei vielen typischen Designs kann es als im Wesentlichen konstant angesehen werden. Daher kann man leicht verstehen, dass das elektromagnetische Drehmoment nur mit dem Statorstrom variiert.

Die Plots des Rotordrehmoments, der Eisen- und der Kupferverluste gegen die Rotordrehzahl und den Statorstrom können verwendet werden, um empirische Beziehungen zu erhalten und eine Effizienzkarte des Motors zu erstellen. Die entsprechenden Ausdrücke für die Rotordrehmomentkonstante, Eisenverluste, Kupferverluste und den Wirkungsgrad lauten:

 
In diesem Fall ist k_1 = 0.07 N.m/A, k_2 = 0.204 W/rps ist die durchschnittliche Steigung und k_3 = 0.164 W/A².

Es ist besonders interessant, die analytisch erstellte Effizienzkarte (unter Verwendung der empirischen Koeffizienten k_1,k_2,k_3) mit der Karte aus der parametrischen Analyse unseres Motormodells zu vergleichen.

Untersuchung des Temperaturanstiegs mit COMSOL Multiphysics^®

Der Temperaturanstieg wirkt sich auf verschiedene Aspekte der Motorleistung aus. Bei Dauermagneten kann ein Temperaturanstieg von, sagen wir, 20 Grad auf 120 Grad einen Rückgang der magnetischen Flussdichte um bis zu 30 % verursachen. Dies führt zu einer entsprechenden Verringerung des Rotordrehmoments und des daraus resultierenden Wirkungsgrads, die ebenfalls bis zu 30 % betragen kann. Der maximal zulässige Temperaturanstieg wird in der Regel unter Berücksichtigung der Isolationsklasse der Statorwicklungen und der Entmagnetisierungsgrenze des Permanentmagnetmaterials bestimmt. Erfahrungsgemäß verkürzt sich die Lebensdauer der Isolierung mit jedem Temperaturanstieg um 10 Grad über dem zulässigen Grenzwert um die Hälfte. Wenn die Temperatur unter extremen Belastungsbedingungen die Isolationsgrenze überschreitet, kann dies zu einem Ausfall der Isolation, einem Kurzschluss zwischen den Wicklungen und schließlich zum Durchbrennen der Statorspulen führen.

Die mit der Unterfunktion Loss Calculation berechneten Eisen- und Kupferverluste können mit dem Interface Heat Transfer (HT) gekoppelt werden, um die thermische Leistung zu analysieren. Das Interface Heat Transfer in COMSOL Multiphysics^® bietet mehrere Möglichkeiten, die Kühlung der Maschine zu untersuchen. Die Modellierung der natürlichen oder erzwungenen Konvektion kann entweder implizit durch Verwendung eines Wärmetransportkoeffizienten von den äußeren Oberflächen oder explizit durch Modellierung einer laminaren oder turbulenten Strömung über die äußeren Motoroberflächen erfolgen. Eine vergleichende Studie der stationären Temperatur kann unter verschiedenen Kühlbedingungen durchgeführt werden, um die am besten geeignete Kühlmethode für eine bestimmte Motoranwendung zu bestimmen.

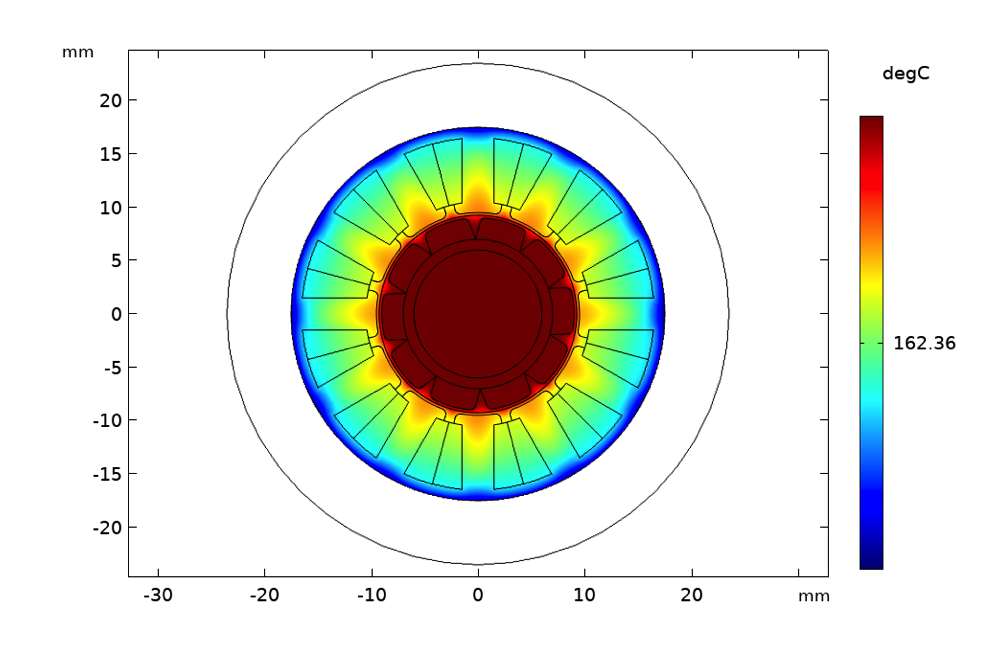
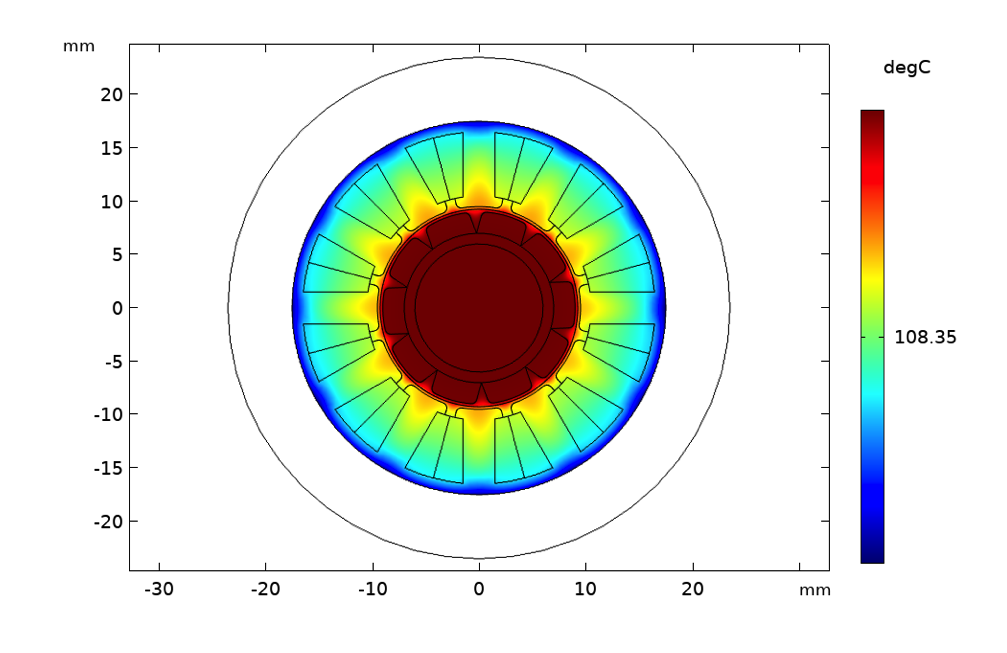
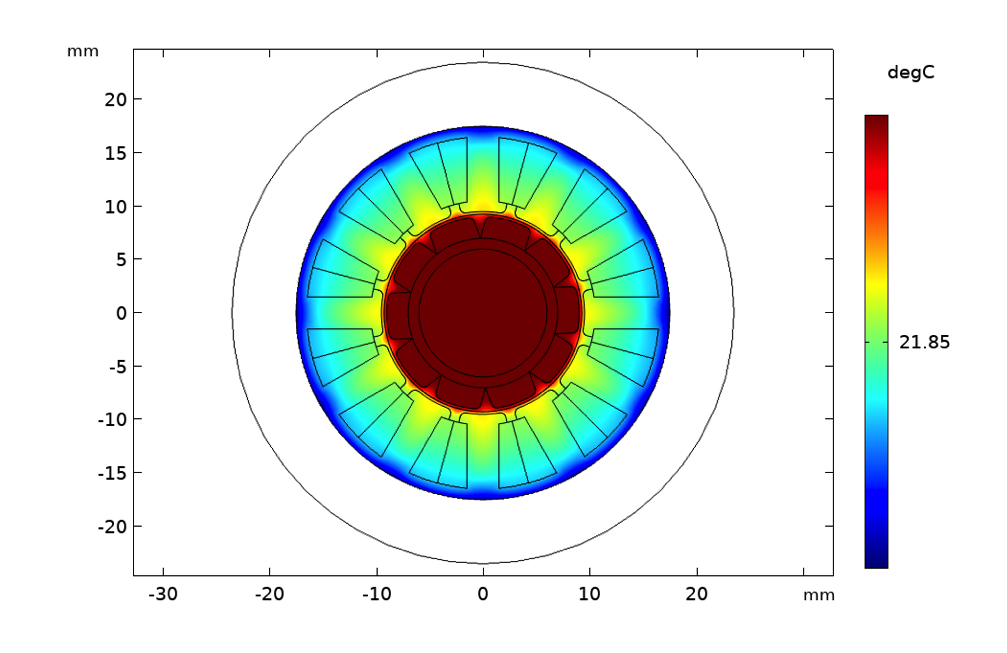
Temperaturanstieg bei natürlicher Luftkonvektion (links), erzwungener Luftkonvektion mit einer Strömungsgeschwindigkeit von 1 m/s (Mitte) und erzwungener Wasserkühlung mit einer Strömungsgeschwindigkeit von 50 mm/s (rechts).

Die Surface Plots zeigen die Temperatur in Grad bei einer Rotordrehzahl von 3000 U/min und einem Statorstrom von 2 A. Die bei natürlicher Konvektion benötigte Isolationsklasse 180 (H) lässt sich in diesem Fall durch eine einfache Sichtprüfung ermitteln. Bei erzwungener Konvektion reduziert sich der Isolationsbedarf auf Klasse 130 (B) und bei Wasserkühlung ist eine Isolation der Klasse 105 (A) ausreichend. Wir gehen hier davon aus, dass das Material der Permanentmagnete unter Berücksichtigung der thermischen Entmagnetisierungseffekte angemessen ausgewählt wurde.

Untersuchung des Wirkungsgrads von Elektromotoren

Letztendlich geht es bei der Analyse eines Motordesigns darum, seinen Wirkungsgrad zu ermitteln. Dieser gibt Aufschluss darüber, welcher Anteil der Eingangsleistung als mechanische Ausgangsleistung gewonnen wird. Der Wirkungsgrad einer rotierenden Maschine variiert mit dem erzeugten elektromagnetischen Drehmoment und der Rotordrehzahl. Im Idealfall sollte die Maschine mit maximalem Wirkungsgrad betrieben werden, aber in der Praxis muss auch die Drehmoment-Drehzahl-Kurve der vom Motor angetriebenen Last berücksichtigt werden. Infolgedessen wird der Motor in einem gewissen Betriebsbereich genutzt. Der nächstbeste Ansatz besteht darin, einen Motor zu wählen, der in diesem Betriebsbereich die höchsten Effizienzwerte aufweist.

An dieser Stelle tritt die Effizienzkarte in den Vordergrund. Die Effizienzkarte eines Motors ist ein Plot des Wirkungsgrads in Abhängigkeit von der Variation der Rotordrehzahl und dem elektromagnetischen Drehmoment. Anders gesagt kann es auch als Plot des Wirkungsgrads im Zustandsraum von Drehmoment und Drehzahl beschrieben werden. Die Effizienzkarte kann mit der Lastkennlinie überlagert werden, um den Gesamtwirkungsgrad des Systems für die gegebene Lastkurve zu bestimmen.

Die Last für Elektrofahrzeuge wird durch Fahrzyklen mit Drehmoment und Drehzahl charakterisiert. Der Fahrzyklus besteht aus dem Drehmoment der Last und der zeitlichen Variation der Drehzahl. Zu jedem Zeitpunkt gibt eine Kombination aus Drehmoment- und Drehzahlwert das Verhalten der Last an. Das Streudiagramm all dieser Drehmoment-Drehzahl-Datenpunkte auf der Effizienzkarte hilft bei der Bestimmung des Gesamtwirkungsgrads, den der Motor für einen bestimmten Fahrzyklus bietet. Dies ermöglicht die Abschätzung der Gesamtenergie, die der Motor während des gesamten Fahrzyklus verbraucht, und folglich die Vorhersage der Reichweite des Elektrofahrzeugs nach einer einzigen Aufladung.

COMSOL Multiphysics^® bietet integrierte Modellierungsfeatures, mit denen Sie ganz einfach die Effizienzkarte für Ihr Motordesign erstellen können. Das Feature Force Calculation berechnet das elektromagnetische Drehmoment. Die Unterfunktion Loss Calculation hilft bei der Ermittlung der Eisen- und Kupferverluste. Das Interface Heat Transfer kann zur Berechnung des verlustbedingten Temperaturanstiegs verwendet werden, wobei eine vollständige Kopplung mit dem Interface Rotating Machinery, Magnetic unter dem Knoten Multiphysics möglich ist, um die elektromagnetischen Effekte des Temperaturanstiegs einzubeziehen. Schließlich ermöglicht das Feature Table Graph das Erstellen der Effizienzkarte.

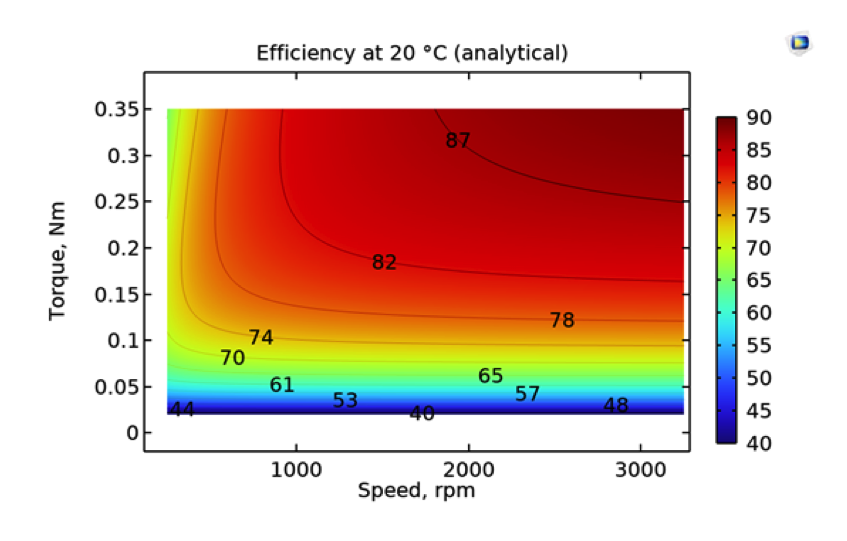
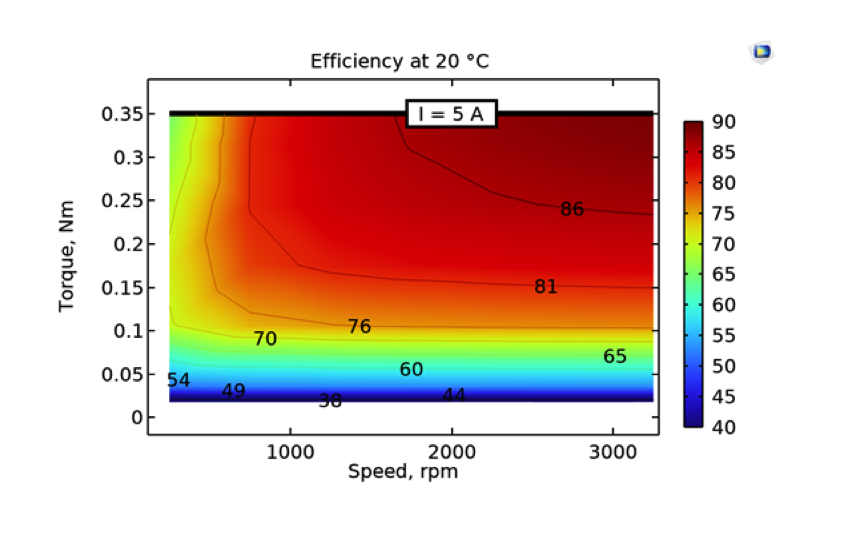
Eine analytisch erstellte Effizienzkarte mit empirischen Koeffizienten (links) und eine aus einer parametrischen Simulation gewonnene Effizienzkarte.

Hier zeigen alle Effizienzkarten den prozentualen Wirkungsgrad. Wie im ersten Abschnitt erläutert, wurde die erste Effizienzkarte analytisch erstellt. Die zweite Effizienzkarte wurde direkt aus einer parametrischen Analyse gewonnen. Die horizontale Linie am oberen Rand des Plots zeigt, dass das maximale Drehmoment einem Statorstrom von 5 A entspricht. Die analytische und die numerische Effizienzkarte zeigen eine gute Übereinstimmung.

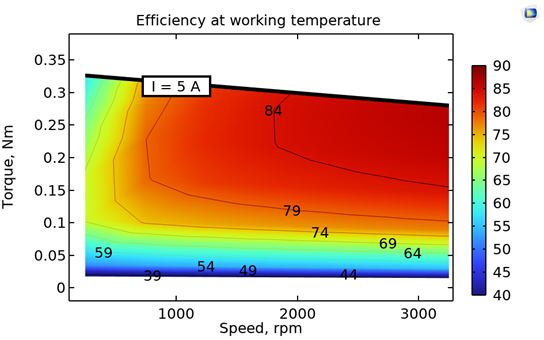
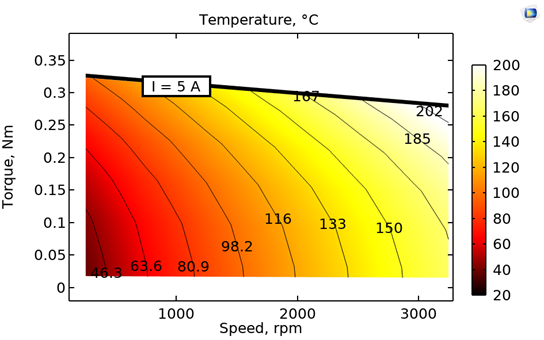
Eine aus Simulationen gewonnene Effizienzkarte, die die Auswirkungen des Temperaturanstiegs berücksichtigt (links), und eine Motortemperaturkarte (rechts).

Im Gegensatz zu den ersten beiden Effizienzkarten beinhaltet die dritte Karte den Effekt des Temperaturanstiegs bei natürlicher Luftkonvektionskühlung. Es ist eine Verringerung der durchschnittlichen Rotordrehmomentwerte für denselben Bereich von Statorstromwerten zu beobachten, nachdem der Effekt des Temperaturanstiegs berücksichtigt wurde. Außerdem sinkt das Drehmoment mit der durch höhere Drehzahlen ansteigenden Temperatur (infolge der erhöhten Verluste) weiter, da der remanente Fluss in den Permanentmagneten des Rotors abnimmt. Dies kann man an der Linie für “I = 5A” im oberen Teil des Plots erkennen. Das Nettoergebnis ist eine Änderung der Effizienzverteilung aufgrund des Temperaturanstiegs. Dadurch lässt sich die Eignung eines bestimmten Motordesigns für die betreffende Anwendung besser beurteilen. Die Temperaturkarte zeigt die durchschnittliche Statortemperatur. Sie erleichtert die Bestimmung der erforderlichen Isolationsklasse und des Materials der Dauermagnete, indem sie sich auf den relevanten Betriebsbereich des Motors konzentriert.

Schlussbemerkungen

Wir haben einen kurzen Blick auf die Energiebilanz im Rahmen von Motorsimulationen geworfen. Eine solche Überprüfung der Energiebilanz hilft Ihnen, die Ergebnisse eines beliebigen FEM-Simulationstools auf ihre Richtigkeit zu überprüfen.

Mithilfe von parametrischen Analysen können die Variation des elektromagnetischen Drehmoments und die Eisen- und Kupferverluste mit der Rotordrehzahl und dem Statorstrom untersucht werden. Durch solche Analysen können die Drehmomentkonstante und empirische Koeffizienten extrahiert werden, um die Verluste bei jeder Drehzahl und dem Stromwert für ein gegebenes Motordesign zu schätzen.

Wir haben den Temperaturanstieg aufgrund von Verlusten in Motoren untersucht, welcher einen großen Einfluss auf das elektromagnetische Drehmoment, den Wirkungsgrad und die erforderliche Isolationsklasse und das Material der Permanentmagnete hat. Eine komparative Studie des Temperaturanstiegs unter verschiedenen Kühlbedingungen erleichtert die Auswahl einer geeigneten Kühlmethode.

Schließlich haben wir Effizienzkarten diskutiert, die bei der Entscheidung, ob ein bestimmtes Motordesign den Anforderungen einer Anwendung entspricht, eine entscheidende Rolle spielen. Die Prüfung der Effizienzkarte unter Berücksichtigung des Temperaturanstiegs ermöglicht es uns, die Leistung der Maschine im Hinblick auf die vorgesehene Anwendung genauer zu beurteilen.

Versuchen Sie es selbst

Probieren Sie selbst aus, den Verlust, die Temperatur und den Wirkungsgrad eines Elektromotors zu berechnen. Klicken Sie auf diese Schaltfläche, um die MPH-Datei für das hier behandelte Modell zu öffnen: