Veröffentlichungen und Präsentationen

The storage of CO2 in the sub-surface is seen as a technology that can contribute to the generally accepted goal of a de-carbonized society. As real field experiments are hardly feasible, many current studies utilize the capabilities of numerical modelling. Concerning the practical application of CO2 storage many questions are still unanswered. In the most favoured scenario CO2 concentrated in brine is pressed into a deep geological formation. Eventually the brine will start to dissolve into deeper formations by diffusion. Increasing concentrations in the lower permeable layer will induce convective patterns, which in turn influence the diffusive transport into the aquifer.
Convection is a multi-physics phenomenon, in which flow and transport processes are coupled with the fluid density is the crucial coupling parameter. For the highly dynamic processes of CO2 storage the initial phase with pure diffusion is followed by a convection phase. The latter can be sub-divided in an early stage with high but fluctuating mass transfer; and a late stage, in which mass transfer is decreasing. Anisotropy and inhomogeneity of the geological formation strongly influence the spatial and temporal dynamics of these processes. 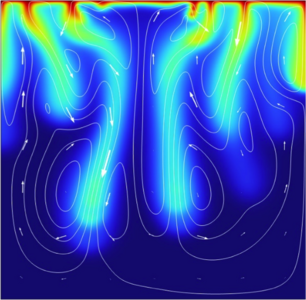The various stages are simulated using the multiphysics capabilities of COMSOL. In the model inhomogeneity is realized by random distributions. Anisotropies are considered to be present in the permeability and the effective diffusivity of the formation. The model results reveal strong fingering patterns (Figures 1 and 2) that effect the brine transfer into the system, represented by the dimensionless Sherwood number Sh. Figure 3, that depicts the development of Sh in time, results from various runs of the model. Clearly the initial diffusive stage (with decreasing Sh) can be identified, as well as the sharp increase with the onset of fingering. With more brine content within the formation Sh finally decreases. Solid lines represent the homogeneous situation with different anisotropy ratios. Dots (in same colour) show the deviation from the homogeneous case, if the aquifer is inhomogeneous.
In summary: the duration of the stages and the size of brine entering the system depend strongly on direction dependence and disturbances of the physical parameters. Despite the differences in the single scenarios the duration of the early diffusion stage as well as the time and amount of maximum brine transfer turn out to vary slightly. In the late convection stage the range of fluctuations is decreasing and at the final simulated time the Sh numbers end up in a similar range.