Veröffentlichungen und Präsentationen

In inductive heating simulations the electromagnetic properties of the steel have a significant impact on the temperature pattern along the heated product. Indeed, taking into account the non-linearity of the ferromagnetic material properties is a key point to have relevant simulation results. In particular, it is important to correctly include the nonlinear relationship between the magnetic flux and the magnetic field intensities through a variable relative permeability. Unfortunately, finding the exact solution to this problem implies the use of time-dependent solvers which lead to extremely high computation times.

In order to overcome this difficulty, a method extracted from literature was successfully implemented in COMSOL Multiphysics® software [1]. The method consists in solving the problem by “considering an equivalent fictitious material where the relative permeability is assumed to be constant in time but different from point to point and is related to the nonlinear B-H characteristics curve with help of the stored magnetic co-energy density”.

This method introduces an effective equivalent magnetic permeability and a fictive maximal magnetic field. Figure 1 synthesizes the different steps of the iterative procedure (for more details see [1]). This iterative procedure has been implemented in COMSOL using segregated solvers.

Concretely, as depicted in Figure 2, the study is shared in two steps. The first one is a frequency resolution, this is dedicated to solve the potential vector A and fictive magnetic permeability while the second one is a time dependent resolution devoted to solve thermal pattern.

The geometry on which the iterative method has been tested is composed of a three turns coil and a pipe surrounded by air. The coil is made of copper whereas the pipe is made of steel. The frequency is set equal to 50 Hz. The model is a 2D axisymmetrical model.

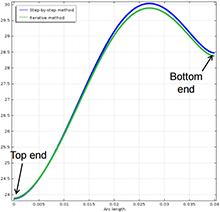
The results obtained by the iterative method have been compared to the classical step by step solution. The comparison has been done in terms of temperature pattern and computational time. The graphs hereafter present the temperature after 5 seconds of inductive heating. The initial pipe temperature is set equal to 20°C.

As shown in Figure 3 and Figure 4, the agreement between the two methods is very good. After 5 seconds the maximal temperature difference is 0.2°C. More precisely, at the middle of the coil the mean temperature of the pipe wall is 29°C instead of 29.2°C that mean a difference of 2%.

The computational times for iterative and classical method are respectively are 39s and 1hr 30min that mean the computational time of the iterative method is 140 times faster than the classical step by step method.

To conclude: the implementation feasibility has been proven for a simple geometry. The results provided by the iterative method are very promising. Indeed, compared with the classical step by step method the computational time is 140 times faster and the pipe warming difference is only 2% in comparison to the classical step by step solution.