Veröffentlichungen und Präsentationen

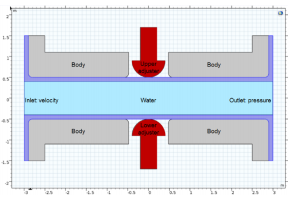
Valves are widely used to control fluid flow in various engineering applications. It’s crucial to study the flow characteristics inside the valve and the fluid-structure interaction between the fluid and valve’s sleeve for design, optimization and improvement of valves. However, because of complex valve geometry, complicated contact status, large deformation, nonlinear material characteristics and fast fluid flow, it is still a big challenge for scientists and engineers to well understand all the necessary mechanical phenomena no matter via experiment or simulation.

The interaction between the fluid and the valve sleeves is two-way coupled: the fluid pressure influences the deformation of the valve sleeves, and the deformation/displacement of valve sleeves influence the fluid flow. Thus, three physics types in COMSOL Multiphysics are added to perform the 2-way coupling analysis: Laminar flow, Solid Mechanics, and Moving Mesh. The valve sleeves have surface contact with the other parts of the valve and especially are pushed by the valve actuators to control the opening percentage of the valve with a large deformation. The contact pressure method is defined as the Augmented Lagrangian method. The sleeves are predicted by Mooney-Rivlin (two parameters) hyperealstic material model. Piecewise functions are set up to define the movements of the valve sleeves. In the Moving Mesh physics, the inlet and outlet defined in Laminar Flow physics are defined with prescribed mesh displacement with a zero value, while the wall (between the fluid and valve sleeves) defined in Laminar Flow physics are defined with prescribed mesh displacement. An example is presented to show the modeling method has the ability of predicting complicated fluid-structure interaction including hyperelastic material model and contact analysis.

After this topic, the audiences will be able to apply COMSOL Multiphysics to (1) perform complicated fluid-structure interaction via Multiphysics simulation; (2) define complicated contact pairs; and (3) define multiple time zones for complicated nonlinear FEA.