
Die Eigenfrequenzanalyse ist ein integraler Bestandteil des numerischen Modellierungs-Toolkits. Die Eigenmoden eines linearen Systems weisen oft unterschiedliche qualitative Merkmale auf und entwickeln sich über einen Parameterbereich, wie beispielsweise die Frequenz, unterschiedlich. Wir werden oft gefragt, ob es eine Möglichkeit gibt, diese Familien von Eigenmodenlösungen über den parametrischen Sweep hinweg zu verfolgen und zu kategorisieren. In diesem Blog-Beitrag zeigen wir, wie dies mit dem Modenüberlappungsintegral in der Software COMSOL Multiphysics® möglich ist.
Eigenmoden und das Überlappungsintegral
Kurzer Test: Was haben die Entwicklung eines Glasfaserkabels für Kommunikationssysteme der nächsten Generation, die Optimierung einer Brückenkonstruktion zur Minimierung unerwünschter mechanischer Resonanzen und die Perfektionierung der akustischen Gestaltung Ihres Wohnzimmers gemeinsam?
In jedem dieser Szenarien müssen wir die Eigenmoden des Systems gut verstehen. Die Eigenmoden sowie die zugehörigen Eigenwerte – die sogenannten Eigenfrequenzen – beschreiben, wie ein lineares System auf externe Anregungen reagiert, und spielen daher eine entscheidende Rolle bei der Gestaltung seines Designs. In bestimmten Fällen möchten wir die Kopplung an eine oder wenige Eigenmoden maximieren, wie zum Beispiel bei einem Hohlraumfilter für die Hochfrequenzkommunikation oder bei einem Lautsprechertreiber. In anderen Situationen kann die Kopplung an diese Resonanzmoden katastrophale Folgen haben, wie zum Beispiel den Einsturz einer Brücke.
Wenn wir die Parameter unseres Systems, wie zum Beispiel die Betriebsfrequenz oder die geometrischen Abmessungen, in einem parametrischen Sweep abstimmen, ändern sich auch die Eigenmoden und Frequenzen. Diese Moden behalten jedoch oft eine qualitative Ähnlichkeit bei. Als einfaches Beispiel betrachten wir die Wellengleichung auf einer elliptischen 2D-Membran – wie die vibrierende Oberfläche eines Trommelfells oder einer Chladni-Platte.
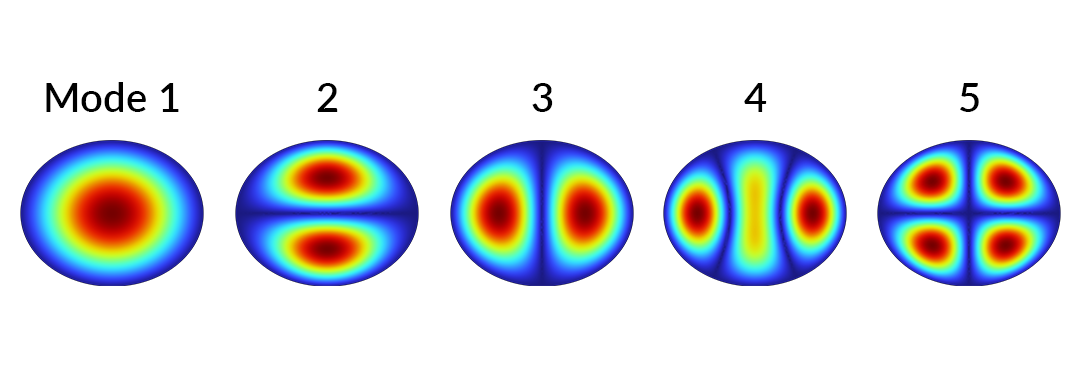
Die ersten fünf Eigenmodenlösungen der 2D-Wellengleichung auf einer elliptischen Membran mit festen Rändern.
Eine Eigenfrequenzstudie zeigt die ersten fünf Eigenmoden, deren Auslenkungen oben dargestellt sind. Lassen Sie uns nun einen Sweep über die vertikale Höhe der Ellipse durchführen.
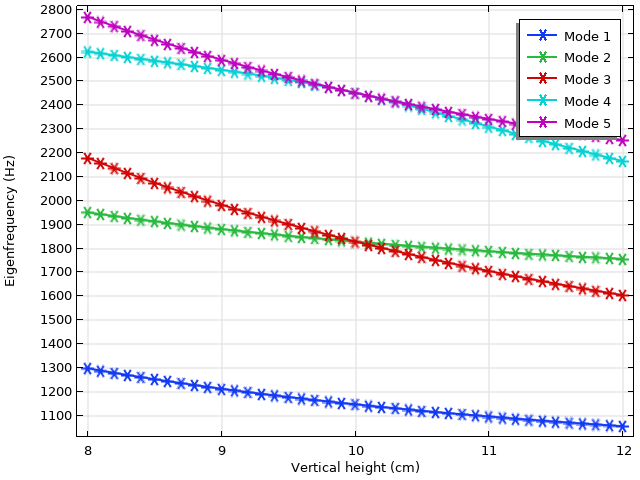
Die Eigenfrequenzen der ersten fünf Moden sind als Plot gegen die vertikale Höhe des elliptischen Gebiets aufgetragen. Beachten Sie die Entartungen zwischen den Moden 2 und 3 sowie zwischen den Moden 4 und 5 bei einer Höhe von 10 cm, wenn das Gebiet perfekt kreisförmig ist.
Die Eigenfrequenzen der ersten fünf Moden sind im obigen Plot dargestellt. Das Modellgebiet ist bei einer vertikalen Höhe von 10 cm perfekt kreisförmig. Dies führt zu Entartungen zwischen den Moden 2 und 3 sowie den Moden 4 und 5. Tatsächlich vertauschen die Moden 2 und 3 nach dem Entartungspunkt die Reihenfolge im Eigenwertplot. Dieses Verhalten ist in vielen Eigenfrequenzstudien zu beobachten. Wie behalten wir diese Moden im Eigenwerteplot im Auge, wenn ihre Reihenfolge durcheinander geraten ist? Um diese Frage zu beantworten, sehen wir uns eine der Moden genauer an.
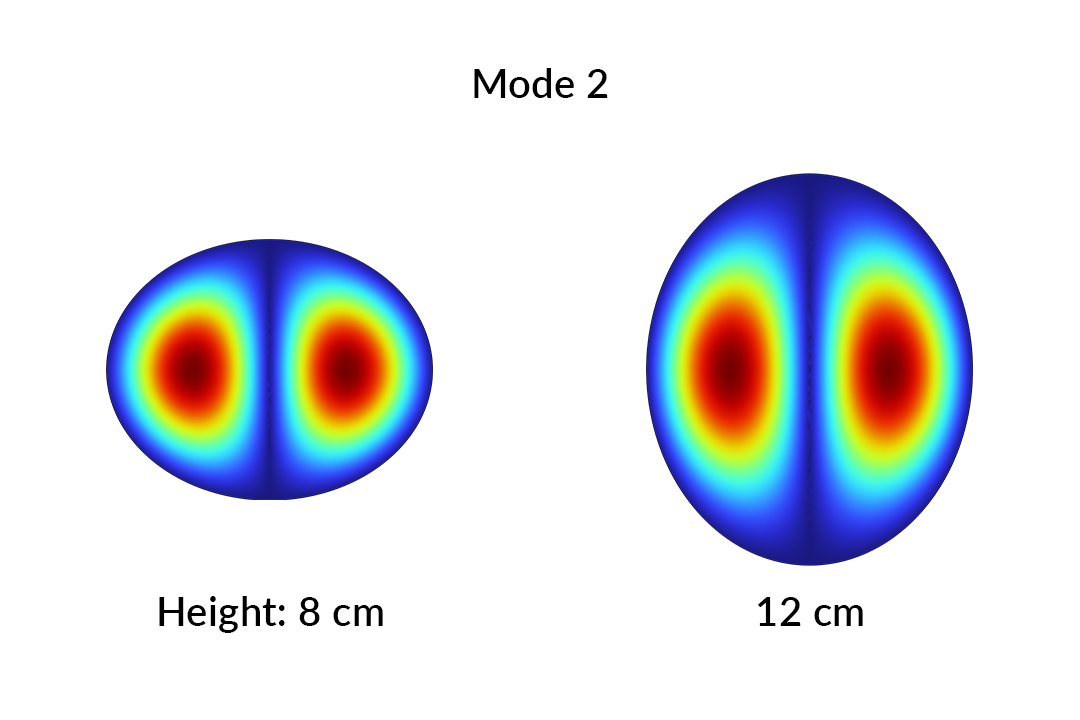
Mode 2 an den beiden Extremen des Parameterbereichs.
Mode 2 ist oben bei einer Höhe von 8 cm und bei einer Höhe von 12 cm dargestellt. Für das menschliche Auge ist die Ähnlichkeit zwischen den Moden offensichtlich. Wir können diese Ähnlichkeit mit dem Modenüberlappungsintegral quantifizieren:
Die Variablen u_i und u_j stellen zwei beliebige Eigenmodenlösungen dar. Der entscheidende Teil dieser Gleichung befindet sich im Zähler: Wir bilden das innere Produkt zwischen den beiden Moden. Der Nenner normalisiert den Wert der Überlappung M, sodass er zwischen 0 und 1 liegt.
Die Überlappung einer Mode mit sich selbst ist 1. Die Überlappung zwischen verschiedenen Eigenmoden bei demselben Parameterwert ist 0, da sie zueinander orthogonal sind. Bei Moden mit unterschiedlichen Parameterwerten liegt M nahe bei 1, vorausgesetzt, die Moden sind qualitativ ähnlich. Beispielsweise haben die beiden oben genannten Moden einen Überlappungswert von M = 0,95, was unsere visuelle Identifizierung bestätigt. Zwei unähnliche Moden haben einen Überlappungswert nahe 0.
Mit dieser Metrik können wir ein Moden-Matching-Schema einrichten, indem wir einen bestimmten Schwellenwert für den Überlappungswert festlegen. Dies kann verwendet werden, um Moden in Dispersionsplots herauszufiltern oder zu gruppieren und sogar automatisch Modenprofilanimationen mithilfe einer Modellmethode zu generieren. In den folgenden Abschnitten werfen wir einen Blick auf diese Strategie und Anwendungen in verschiedenen physikalischen Disziplinen.
Beispiel 1: Ein optisch anisotroper Wellenleiter
In einem früheren Blog-Beitrag zum Thema Modellierung optisch anisotroper Medien haben wir uns mit den Transversalmoden eines optisch anisotropen Wellenleiters befasst. Diese Moden können nach der vorherrschenden Richtung des elektrischen Feldes sowie nach der Anzahl der Amplitudenmaxima in der Transversalebene gruppiert werden. Eine Auswahl der Moden E^x_{ij} ist unten dargestellt.
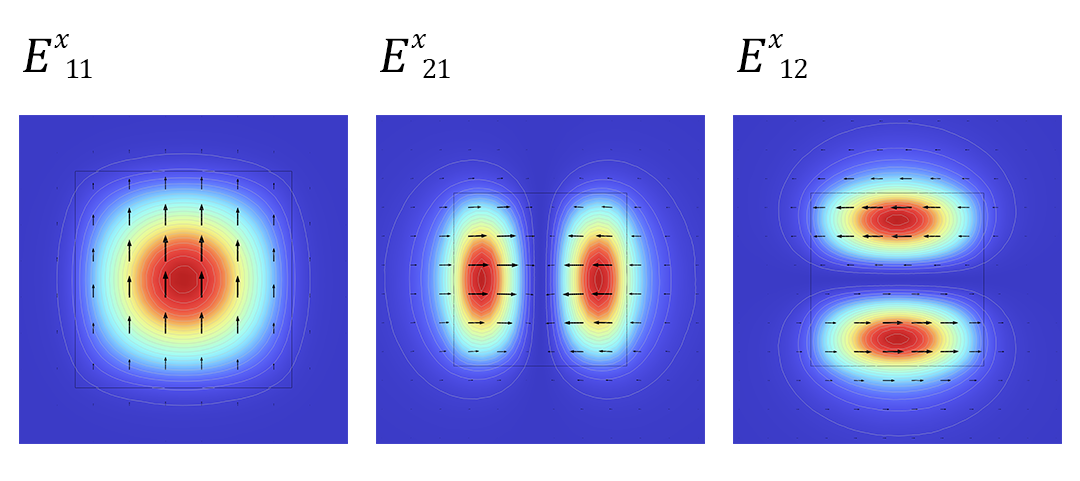
Die ersten drei Eigenmoden E^x_{ij} in einem optisch anisotropen Wellenleiter.
Da der Hauptzweck des Wellenleiters darin besteht, den Lichtfluss zu steuern, ist es entscheidend, das Verhalten dieser Ausbreitungsmoden zu verstehen. Bei jeder Frequenz ist jeder Mode ein effektiver Brechungsindex zugeordnet, der bestimmt, wie schnell sie sich ausbreiten, welche effektive Wellenlänge sie haben und wie stark sie gedämpft werden (wenn im Modell Verluste auftreten). Wir verwenden den Dispersionsplot, um darzustellen, wie sich der effektive Brechungsindex als Funktion der Frequenz ändert.
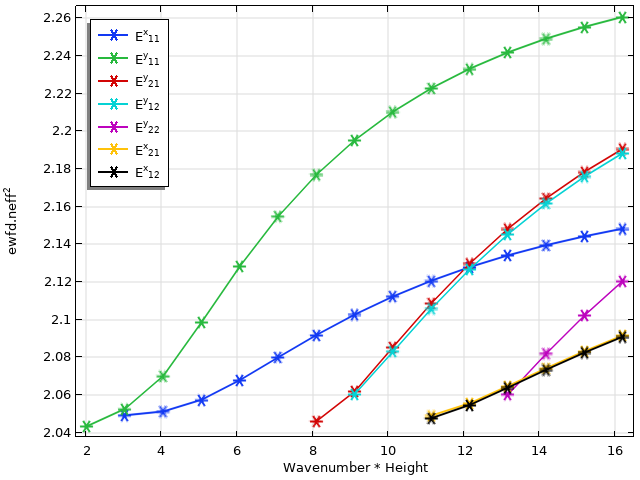
Der Dispersionsplot für den Wellenleiter ist oben dargestellt. Die zahlreichen Modenübergänge machen es erforderlich, die Eigenmoden zu kategorisieren, um sie korrekt zu benennen.
In der Rohausgabe der Modenanalyse-Studie sind die effektiven Brechungsindizes nicht auf sinnvolle Weise gruppiert oder geordnet, da der Löser a priori keine Kenntnis von diesen Moden hat. Wir wenden die Überlappungsintegralberechnung an, um diese Eigenwerte nach Modenprofil zu kategorisieren. Da jeder effektive Indexwert nun mit einer bestimmten Mode von E^x_{ij} oder E^y_{ij} verknüpft ist, können wir ganz einfach Filter und Plot-Optionen verwenden, um jede Mode in den Legenden der Plots farblich zu kennzeichnen und zu kommentieren. Diese Methode ist in der Lage, die mehrfachen Modenübergänge sowie Moden mit sehr nah beieinander liegenden Eigenwerten korrekt aufzulösen, wie zum Beispiel zwischen den Moden E^{x,y}_{12} und E^{x,y}_{21}.
Beispiel 2: Eigenfrequenzen einer rotierenden Schaufel
Das Verständnis der Resonanzmoden eines rotierenden Bauteils, wie zum Beispiel eines Windturbinenblatts oder eines Elektromotors, ist für Anwendungen wie die Stabilitätsanalyse oder die Minimierung von Geräuschen und Vibrationen von entscheidender Bedeutung. Als einfaches Beispiel werfen wir einen Blick auf das Modell Eigenfrequenz einer rotierenden Schaufel in der Application Library.
Wenn die rechteckige Schaufel mit zunehmender Winkelgeschwindigkeit gedreht wird, erwarten wir, dass zwei wesentliche konkurrierende Phänomene dominieren: Spannungssteifigkeit und Spin Softening. Ersteres versteift die Schaufel aufgrund des stationären Spannungsfeldes durch den Zentrifugaleffekt und führt zu einem Anstieg der Eigenfrequenz. Letzteres weicht die Schaufel aufgrund der radialen Bewegungsverstärkung auf, was zu einem Abfall der Eigenfrequenz führt. Das Gleichgewicht dieser Effekte lässt sich am besten in einem Campbell-Diagramm darstellen, in dem die Eigenfrequenzen als Funktion der Winkelgeschwindigkeit dargestellt werden.
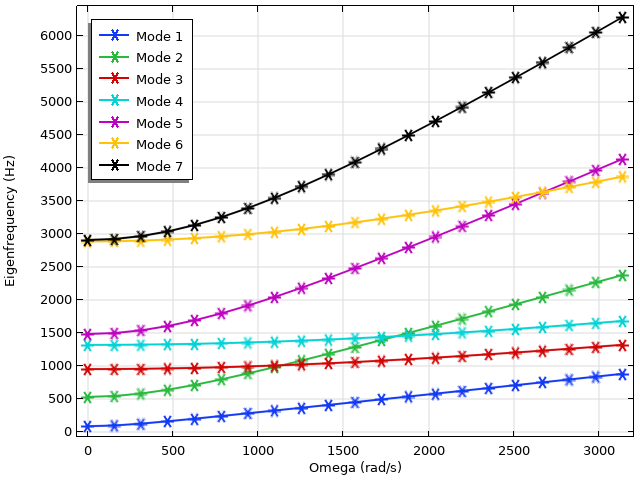
Campbell-Diagramm einer rotierenden Schaufel. Beachten Sie die deutliche Zunahme der Eigenfrequenzen der Moden 2 und 5.
Das Campbell-Diagramm für die ersten sieben Eigenmoden ist oben dargestellt. Im Allgemeinen beobachten wir einen Aufwärtstrend bei den Eigenfrequenzen, was darauf hindeutet, dass die Spannungssteifigkeit eine große Rolle spielt. Dies ist bei den Moden 2 und 5 noch ausgeprägter, deren Eigenwerte dramatisch ansteigen und die der anderen Moden im untersuchten Parameterbereich überkreuzen. Die Verschiebung und Spannungen der ersten sechs Moden sind unten dargestellt.
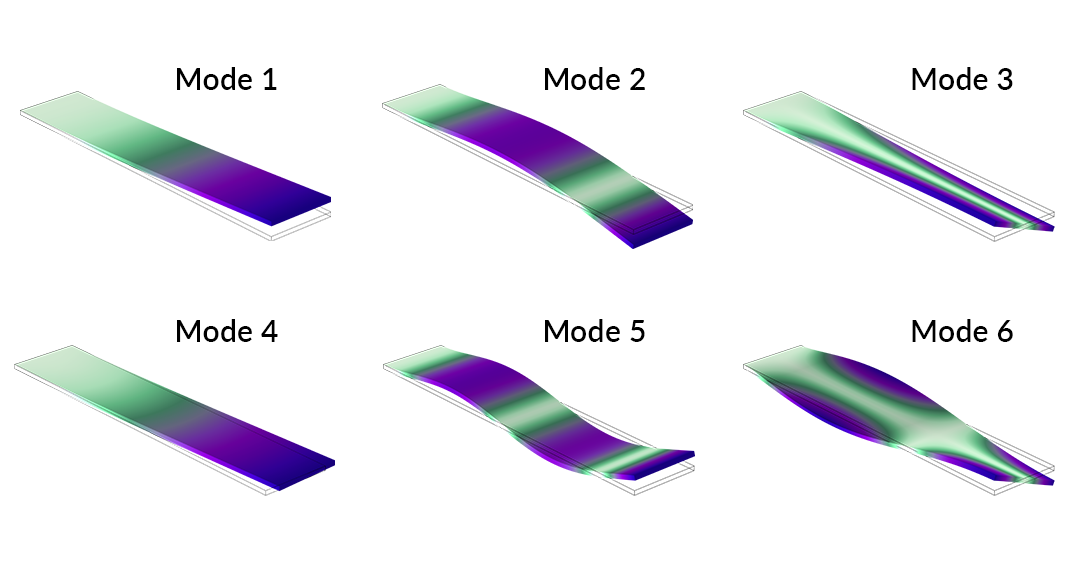
Die ersten sechs Eigenmoden einer rotierenden Schaufel.
In einem komplexeren System kann das Campbell-Diagramm dichter mit Eigenfrequenzen gefüllt sein, die sowohl steigende als auch fallende Trends aufweisen. Das Verständnis und die Visualisierung dieser Trends ist wichtig, beispielsweise bei der Bestimmung kritischer Geschwindigkeiten. Das Modenüberlappungsintegral erleichtert die Kategorisierung und Verfolgung des Verhaltens dieser Modenfamilien.
Beispiel 3: Eigenmoden in einem Schalldämpfer mit elastischen Wänden
Die Multiphysik-Simulation spielt eine entscheidende Rolle bei der Konstruktion von Schalldämpfern für Verbrennungsmotoren. Neben der Modellierung von Druckwellen in der Luftmasse muss auch die Wechselwirkung der Luftmasse mit dem Schalldämpfergehäuse berücksichtigt werden. Dies führt zu einem genaueren Übertragungsprofil über den gesamten Frequenzbereich.
Eine Auswirkung der Akustik-Struktur-Interaktion ist die Einführung vieler weiterer Resonanzmoden, wie in diesen beiden Beispielen dargestellt: Eigenmoden in einem Schalldämpfer und Eigenmoden in einem Schalldämpfer mit elastischen Wänden. Schauen wir uns das zweite Modell genauer an. Wir führen eine Modenanalyse des Schalldämpferquerschnitts über einen Frequenzbereich durch, um die Modenprofile und ihre entsprechenden Grenzfrequenzen zu bestimmen.
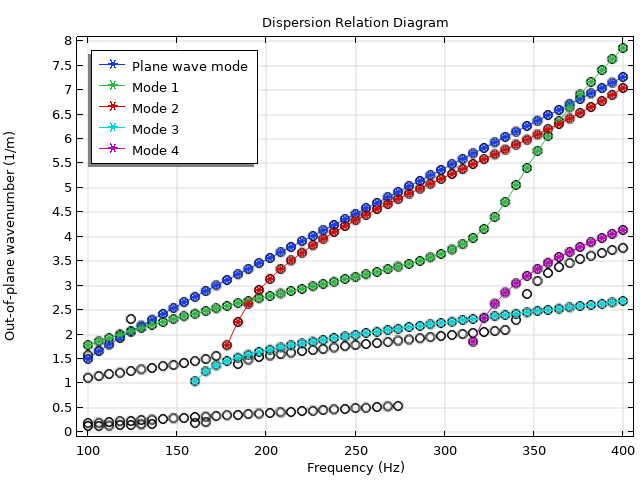
Dispersionsplot des Schalldämpfers mit elastischen Wänden. Neben der ebenen Wellenmode (blau) sind aufgrund der Wechselwirkung zwischen der Luftmasse und den Schalldämpferwänden viele andere Modenfamilien vorhanden. Eine Teilmenge davon wird mithilfe der Modenüberlappungsmethode verfolgt.
Eine Auswahl von Moden und ihre Ausbreitungskonstanten sind im obigen Dispersionsplot gegen die Frequenz aufgetragen. Im Datensatz sind eindeutig Trends zu erkennen, die wahrscheinlich bestimmten Modenfamilien entsprechen. Beispielsweise bildet die ebene Wellenmode eine gerade diagonale Linie, die den gesamten Bereich durchschneidet. Durch Anwendung des Überlappungsintegrals können wir das erwartete Verhalten der ebenen Wellenmode bestätigen und mehrere andere Moden über den Frequenzbereich hinweg verfolgen. Diese Modenprofile sind unten dargestellt.
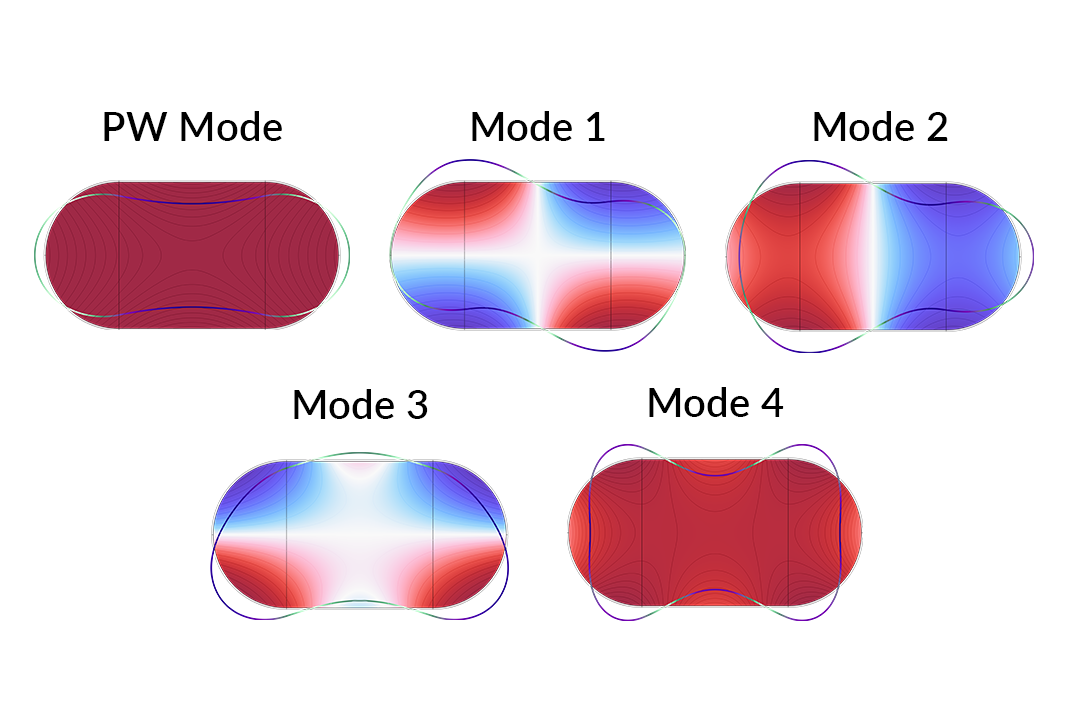
Eine Auswahl von Modenprofilen im Schalldämpfer mit elastischen Wänden.
Mithilfe einer Modellmethode können wir sogar automatisch eine Animation der Modenentwicklung über den Frequenzbereich generieren.
Die Entwicklung von Mode 3 wird mithilfe einer Modellmethode über den gesamten Parameterbereich hinweg verfolgt und animiert.
Die obige Animation zeigt, wie sich Mode 3 von der Nähe ihres Grenzwerts bei 160 Hz bis zur Obergrenze der Studie bei 400 Hz dramatisch verändert und dabei mehrere andere Eigenmoden durchläuft. Die Verfolgung der Entwicklung einzelner Modenfamilien wird mithilfe des Modenüberlappungsintegrals viel einfacher.
Nächste Schritte
In diesem Blog-Beitrag haben wir die Verwendung des Modenüberlappungsintegrals demonstriert, das uns dabei hilft, Moden in Eigenfrequenzstudien zu verfolgen und zu kategorisieren. Wenn Sie mehr über dieses Thema lernen möchten, klicken Sie auf die Schaltfläche unten, die Sie zum entsprechenden Artikel im Learning Center führt:
Die in diesem Blog-Beitrag besprochenen Modelle können Sie außerdem in der Application Gallery herunterladen:
- Optisch anisotroper Wellenleiter
- Eigenfrequenz einer rotierenden Schaufel
- Eigenmoden in einem Schalldämpfer mit elastischen Wänden



Kommentare (0)