In dieser Blog-Serie werden wir die Simulation von Ionen- oder Elektronenstrahlen mithilfe von Teilchenverfolgungstechniken untersuchen. Wir beginnen mit einigen Hintergrundinformationen zu Wahrscheinlichkeitsverteilungsfunktionen und den verschiedenen Möglichkeiten, wie Sie in der COMSOL Multiphysics® Software Zufallszahlen aus diesen Funktionen ziehen können. In späteren Kapiteln werden wir zeigen, wie die zugrunde liegende Mathematik verwendet werden kann, um die Ausbreitung von Ionen- und Elektronenstrahlen in realen Systemen genau zu simulieren.
Die Motivation für die Verwendung von Wahrscheinlichkeitsverteilungsfunktionen
Energetische Ionen- und Elektronenstrahlen sind ein Thema von großem Interesse in der Grundlagenforschung der Teilchen- und Kernphysik. Sie werden aber auch in einer Vielzahl von Anwendungsbereichen genutzt, darunter Kathodenstrahlröhren, die Herstellung medizinischer Isotope und die Behandlung von Atommüll. Bei der genauen rechnerischen Modellierung der Strahlenausbreitung sind die Anfangswerte der Teilchenposition und der Geschwindigkeitskomponenten von besonderer Bedeutung.
Wenn wir Ionen oder Elektronen in einem Strahl für eine Teilchenverfolgungssimulation freisetzen, müssen wir diese Partikel oft als diskrete Punkte im Phasenraum erfassen. Bevor wir uns jedoch zu sehr damit beschäftigen, was der Phasenraum ist und was Ionen oder Elektronen mit ihm zu tun haben, wollen wir mehr über Wahrscheinlichkeitsverteilungsfunktionen erfahren und wie sie in COMSOL Multiphysics® genutzt werden können.
Eine Einführung zu Wahrscheinlichkeitsverteilungsfunktionen
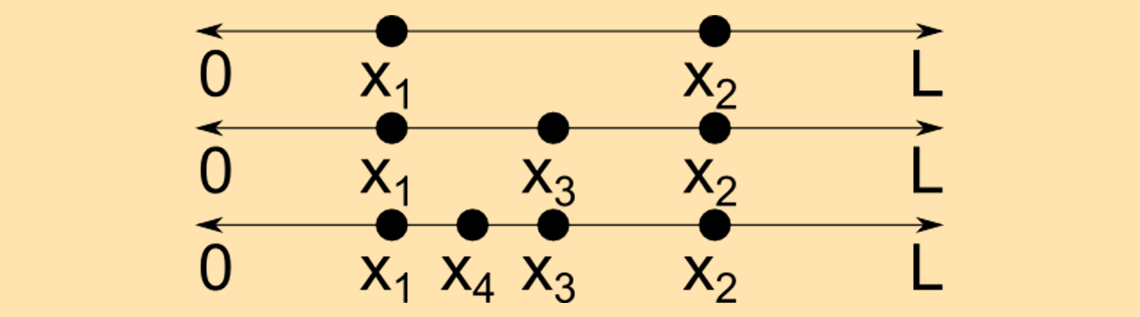
Lassen Sie uns mit ein paar Definitionen beginnen. Eine kontinuierliche Zufallsvariable x ist eine Zufallsvariable, die unendlich viele Werte annehmen kann. Nehmen wir zum Beispiel an, dass ein Punkt x1 zufällig entlang eines Liniensegments der Länge L ausgewählt wird. Dann wird ein zweiter Punkt x2 an einer anderen Stelle entlang dieser Linie ausgewählt. Unter der Annahme, dass diese beiden Punkte unterschiedlich sind, können wir dann einen dritten unterschiedlichen Punkt x_3 = (x_1+x_2)/2 auswählen, der ebenfalls auf der Linie liegt, dann einen vierten Punkt x_4 = (x_1+x_3)/2 und so weiter, so dass wir unendlich viele unterschiedliche Punkte erhalten können. Dies wird im Folgenden veranschaulicht.
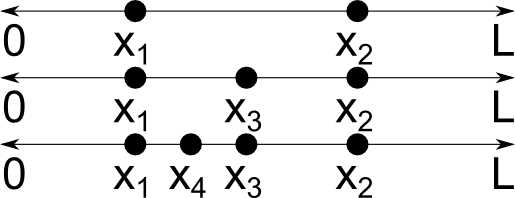
Die andere Art von Zufallsvariable wird übrigens diskrete Zufallsvariable genannt und kann nur bestimmte Werte annehmen. Denken Sie an das Werfen einer Münze oder das Ziehen einer Karte aus einem Stapel; die Anzahl der Ergebnisse ist endlich.
Eine 1D-Wahrscheinlichkeitsverteilungsfunktion oder Wahrscheinlichkeitsdichtefunktion f(x) beschreibt die Wahrscheinlichkeit, dass der Wert der kontinuierlichen Zufallsvariablen einen bestimmten Wert annimmt. Zum Beispiel beschreibt die Wahrscheinlichkeitsverteilungsfunktion
(1)
\begin{array}{cc}
0 & x\leq 0\\
1 & 0\textless x \textless 1\\
0 & 1\leq x
\end{array}
\right.
eine Variable x, die eine gleichmäßige Chance hat, einen beliebigen Wert im offenen Intervall (0, 1) anzunehmen, aber keine Chance hat, einen anderen Wert anzunehmen. Diese Wahrscheinlichkeitsverteilungsfunktion, eine Gleichverteilung, ist unten abgebildet.
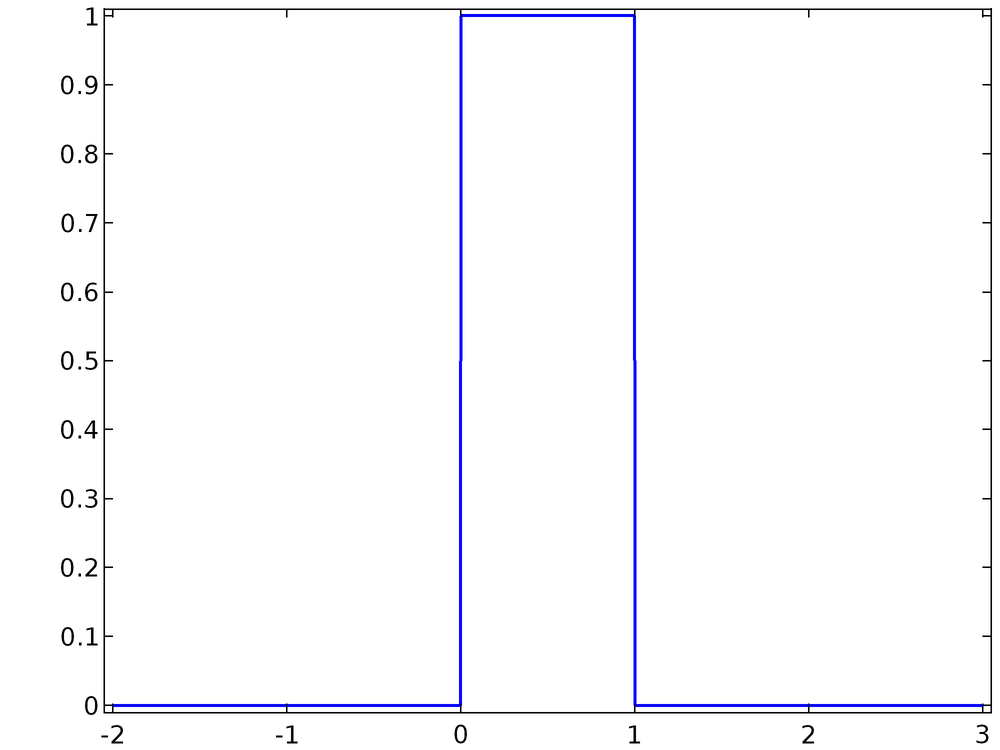
Wahrscheinlichkeitsverteilungsfunktionen können auch auf diskrete Zufallsvariablen angewandt werden, und sogar auf Variablen, die in einigen Intervallen kontinuierlich und in anderen diskret sind. Eine alternative Möglichkeit, eine solche Zufallsvariable zu interpretieren, besteht darin, sie als kontinuierliche Zufallsvariable zu behandeln, für die die Wahrscheinlichkeitsverteilungsfunktion eine oder mehrere Dirac-Delta-Funktionen enthält. In dieser Blog-Serie werden wir nur kontinuierliche Zufallsvariablen betrachten.
Die Wahrscheinlichkeitsverteilungsfunktion (WVF) ist normalisiert, wenn
Mit anderen Worten, die Gesamtwahrscheinlichkeit, dass die Variable x einen Wert irgendwo im Bereich (-∞, ∞) annimmt, ist Eins.
Eine kumulative Verteilungsfunktion F(x) ist die Wahrscheinlichkeit, dass der Wert der kontinuierlichen Zufallsvariablen im Intervall (-∞, x) liegt. Die Wahrscheinlichkeitsverteilungsfunktion und die kumulative Verteilungsfunktion (KVF) sind durch Integration miteinander verbunden,
Aus der obigen Definition geht hervor, dass, wenn die WVF normalisiert ist,
Die WVF aus Gleichung (1) und die entsprechende KVF sind unten eingezeichnet. Es ist klar, dass die WVF, wie beschrieben, normalisiert ist.
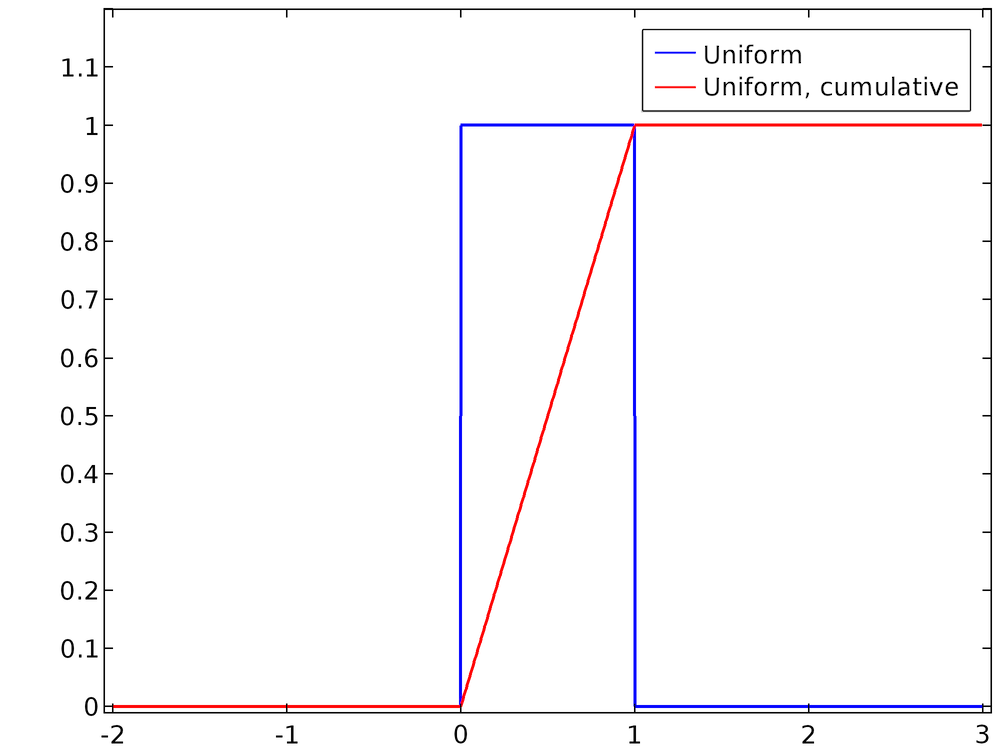
Zufallszahlen aus einer 1D-Verteilung
Die Auswahl eines Zufallswertes aus einer Gleichverteilung ist normalerweise recht einfach. In den meisten Programmiersprachen sind Routinen zur Erzeugung gleichmäßig verteilter Zufallszahlen leicht verfügbar. Nehmen wir jedoch an, dass wir eine viel willkürlichere Verteilung wie die unten gezeigte haben.
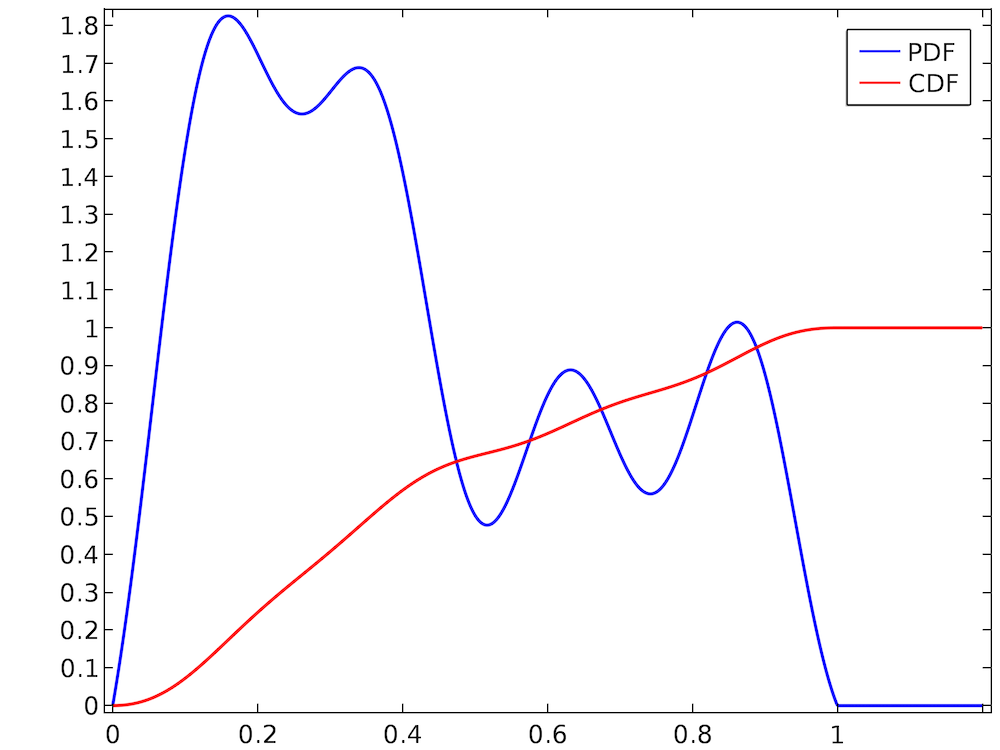
Die Zufallszahl nimmt Werte im Intervall (0, 1) an, und die WVF ist normalisiert, da die KVF bei 1 endet. Die Verteilung ist jedoch eindeutig nicht gleichmäßig. So liegt die Zufallszahl beispielsweise viel eher im Bereich (0.2, 0.3) als im Bereich (0.7, 0.8). Einfach eine eingebaute Routine zu verwenden, die gleichmäßig verteilte Zufallszahlen aus dem Intervall (0, 1) nimmt, wäre nicht korrekt. Daher müssen wir uns alternative Wege überlegen, um Zufallszahlen aus dieser willkürlich aussehenden WVF zu ziehen.
Dies bringt uns zu einer der grundlegendsten Methoden für die Stichprobenziehung von Werten aus einer WVF, der Inversionsmethode. Sei U eine gleichmäßig verteilte Zufallszahl zwischen Null und Eins. (Mit anderen Worten, U folgt der Verteilungsfunktion, die durch Gleichung (1) gegeben ist.) Um eine Zufallszahl mit einer (möglicherweise ungleichmäßigen) WVF f(x) zu erhalten, gehen Sie wie folgt vor:
- Normalisieren Sie die Funktion f(x), wenn sie nicht bereits normalisiert ist.
- Integrieren Sie die normalisierte WVF f(x), um die KVF, F(x), zu berechnen.
- Invertieren Sie die Funktion F(x). Die resultierende Funktion ist die inverse kumulative Verteilungsfunktion oder Quantilsfunktion F-1(x). Da wir f(x) bereits normalisiert haben, können wir dies auch als inverse normale kumulative Verteilungsfunktion oder einfach als inverse normale KVF bezeichnen.
- Setzen Sie den Wert der gleichmäßig verteilten Zufallszahl U in die inverse normale KVF ein.
Zusammengefasst ist F-1(U) eine Zufallszahl mit einer WVF f(x), wenn U \in \left(0,1\right). Schauen wir uns ein Beispiel an, bei dem diese Methode für eine Stichprobe aus einer nicht-gleichverteilten WVF verwendet wird.
Beispiel 1: Die Rayleigh-Verteilung
Die Rayleigh-Verteilung taucht recht häufig in Gleichungen zur Dynamik verdünnter Gase und zur Strahlphysik auf. Sie ist gegeben durch
(2)
\begin{array}{cc}
0 & x\textless 0 \\
\frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right) & x\geq 0
\end{array}
\right.
wobei σ ein noch zu spezifizierender Skalierungsfaktor ist. Wir können überprüfen, ob die Rayleigh-Verteilung, wie oben geschrieben, normalisiert ist,
\int_{0}^{\infty} \frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right)dx
&= \lim_{x \rightarrow \infty} \left.-\exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)\right|^x_0\\
&= 1-\lim_{x \rightarrow \infty}\exp\left(-\frac{x^2}{2\sigma^2}\right)\\
&= 1
\end{aligned}
Die KVF ist
F(x)
&=\int_{0}^{x} \frac{x^\prime}{\sigma^2} \exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)dx^\prime\\
&= \left.-\exp\left(-\frac{x^\prime^2}{2\sigma^2}\right)\right|^x_0\\
&= 1-\exp\left(-\frac{x^2}{2\sigma^2}\right)
\end{aligned}
Für σ = 1 sind die normalisierte Rayleigh-Verteilung und ihre KVF unten eingezeichnet. Für größere Werte von x ist es offensichtlich, dass sich die KVF Eins annähert.
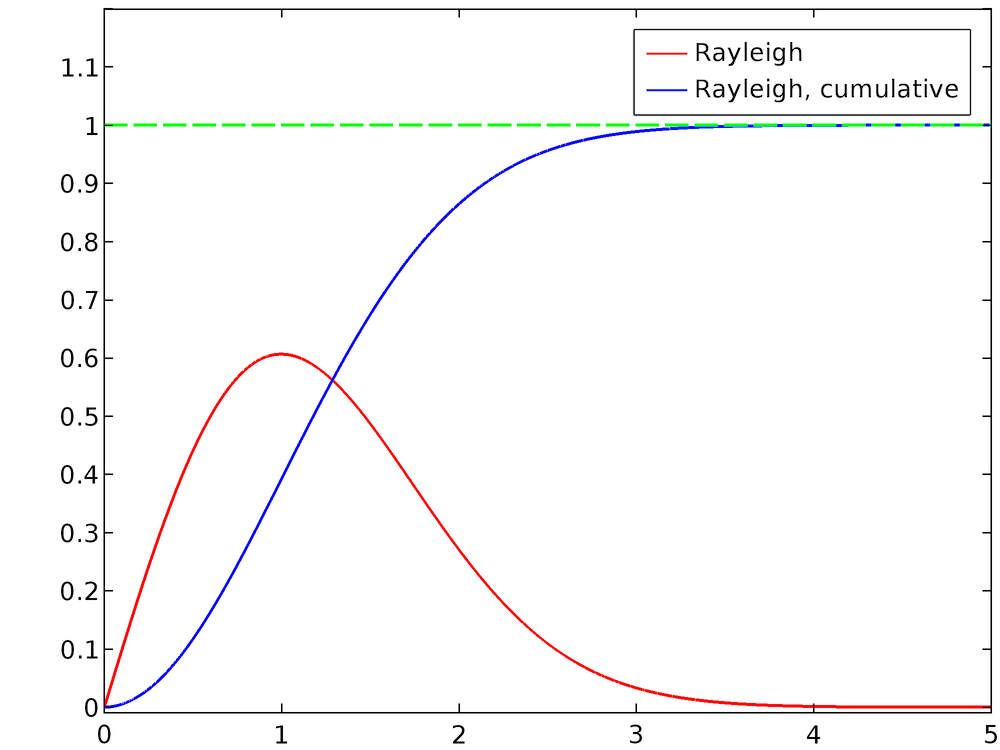
Um die inverse normale KVF zu berechnen, setzen Sie y = F(x) und lösen für x:
y &= F(x)\\
y &= 1-\exp\left(-\frac{x^2}{2\sigma^2}\right)\\
\exp\left(-\frac{x^2}{2\sigma^2}\right) &= 1-y\\
-\frac{x^2}{2\sigma^2} &= \log\left(1-y\right)\\
x &= \sigma \sqrt{-2 \log\left(1-y\right)}
\end{aligned}
Ersetzen Sie nun die Variable y durch die gleichmäßig verteilte Zufallszahl U ,
Da U gleichmäßig im Intervall (0, 1) verteilt ist und sein Wert noch nicht bestimmt wurde, können wir diesen Ausdruck weiter vereinfachen, indem wir feststellen, dass U und 1 – U genau der gleichen WVF folgen. So erhalten wir den endgültigen Ausdruck für den Stichprobenwert von x,
(3)
Als Nächstes werden wir besprechen, wie Gleichung (3) in einem COMSOL-Modell verwendet werden kann, um Werte aus der Rayleigh-Verteilung zu ziehen.
Beachten Sie, dass die inversen normale KVF nicht immer analytisch berechnet werden kann. Es gibt nicht immer eine geschlossene analytische Lösung für das Integral einer beliebigen Funktion, und es ist nicht immer möglich, einen Ausdruck für die Umkehrung der KVF zu schreiben. Die Rayleigh-Verteilung wurde hier absichtlich verwendet, weil ihre inverse normale KVF abgeleitet werden kann, ohne dass dafür numerische oder approximative Methoden nötig sind.
Zufallsstichproben in COMSOL Multiphysics®
Wir können die Ergebnisse der obigen Analyse verwenden, um in COMSOL Multiphysics® eine Stichprobe aus einer beliebigen 1D-Verteilung, z.B. der Rayleigh-Verteilung, zu ziehen. Betrachten wir zunächst die eingebauten Funktionen für das Ziehen aus bestimmten Verteilungstypen.
Es gibt mehrere Möglichkeiten, in COMSOL Multiphysics® Pseudozufallszahlen zu definieren (auf die Bedeutung von “Pseudozufallszahlen” gehen wir später noch ein). Sie können die Funktion Random verwenden, die über die Knoten Global Definitions und Definitions verfügbar ist, um eine Pseudozufallszahl mit einer gleichmäßigen oder normalen Verteilung zu definieren. Wenn eine Gleichverteilung verwendet wird, geben Sie den Mittelwert und den Bereich an. Für einen Mittelwert μu und einen Bereich σu ist die WVF
\begin{array}{cc}
0 & x \leq \mu_u-\frac{\sigma_u}{2}\\
\frac{1}{\sigma_u} & \mu_u-\frac{\sigma_u}{2} \textless x \textless \mu_u + \frac{\sigma_u}{2}\\
0 & \mu_u + \frac{\sigma_u}{2} \leq x\\
\end{array}
\right.
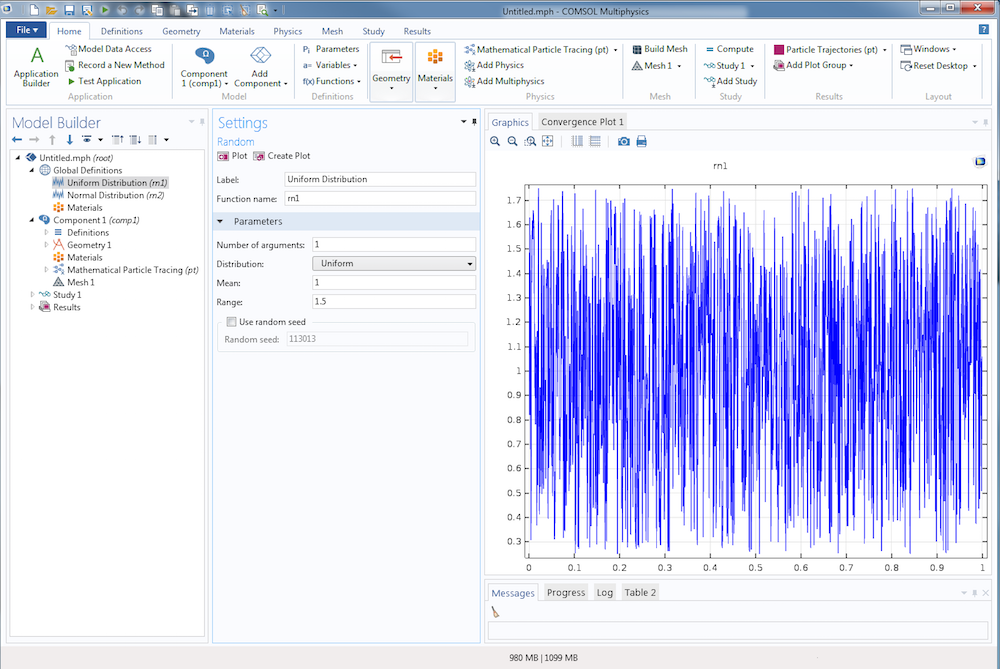
Ein Beispiel für eine Gleichverteilung mit einem Mittelwert von 1 und einem Bereich von 1,5 ist unten abgebildet.
Wenn eine Normal– oder Gaußsche Verteilung verwendet wird, geben Sie den Mittelwert und die Standardabweichung an. Für einen Mittelwert von μn und eine Standardabweichung von σn lautet die WVF
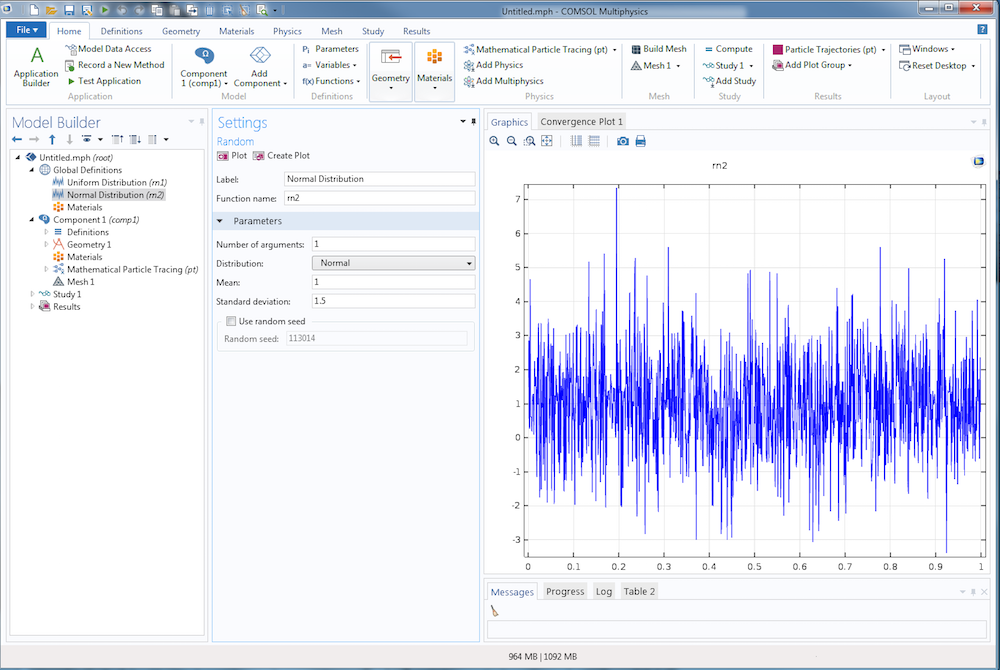
Ein Beispiel für eine Normalverteilung mit einem Mittelwert von 1 und einer Standardabweichung von 1,5 ist unten abgebildet. Wie bei der Gleichverteilung ist die Kurve gezackt und unvorhersehbar. Anders als bei der Gleichverteilung sind die Punkte entlang der Kurve in der Nähe der Linie y = 1 sehr dicht und fallen von dort aus allmählich ab.
Für die Default-Einstellungen, bei denen der Mittelwert 0 und der Bereich oder die Standardabweichung 1 ist, werden die beiden Verteilungen unten verglichen.
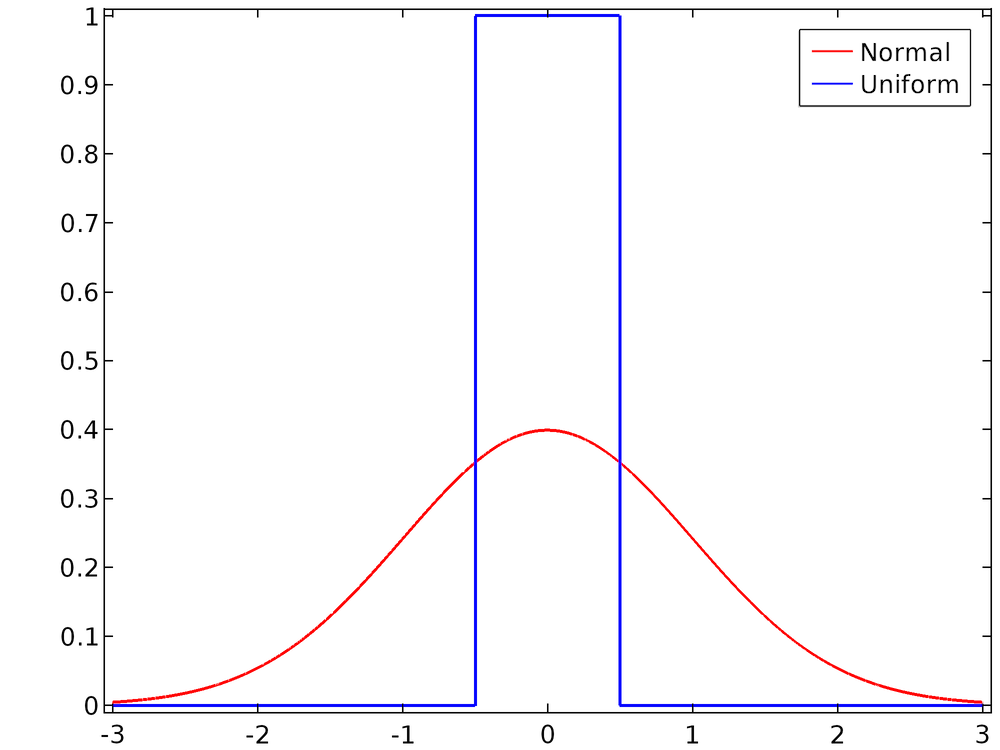
Vergleich der gleichverteilten WVF mit dem Einheitsbereich und der Gaußschen WVF mit der Einheitsstandardabweichung.
Anstatt die Funktion Random zu verwenden, können Sie auch die eingebauten Funktionen random und randomnormal in einem beliebigen Ausdruck verwenden. Die Funktion random ist eine Gleichverteilung mit einem Mittelwert von 0 und einem Bereich von 1. Die Funktion randomnormal ist eine Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1.
Wenn wir uns daran erinnern, dass wir für Gleichung (3) eine Zahl U benötigen, die gleichmäßig aus dem Intervall (0, 1) gezogen wird, haben wir zwei Möglichkeiten:
- Die Funktion Random mit einem Mittelwert von 0,5 und einem Bereich von 1 verwenden.
- Die eingebaute Funktion
randomverwenden und 0.5 hinzufügen.
Im folgenden Fall gehen wir davon aus, dass der zweite Ansatz verwendet wird, obwohl beide möglich sind.
Zufallszahlen, Pseudozufallszahlen und Seeding
Wir haben bereits erwähnt, dass die oben genannten Methoden verwendet werden, um Pseudozufallszahlen zu erzeugen. Pseudozufallszahlen bedeutet, dass die Zufallszahl auf deterministische Weise aus einem Ausgangswert oder Seed erzeugt wird. Bei der eingebauten Zufallsfunktion random ist der Seed das Argument (oder die Argumente) für die Funktion. Im Vergleich dazu können echte Zufallszahlen nicht von einem Programm allein erzeugt werden, sondern erfordern eine natürliche Quelle der Entropie, d.h. einen natürlichen Prozess, der von Natur aus unvorhersehbar und unwiederholbar ist, wie z.B. radioaktiver Zerfall oder atmosphärisches Rauschen.
Es gibt mehrere Gründe, warum es bequemer ist, mit Pseudozufallszahlen als mit echten Zufallszahlen zu arbeiten. Ihre Reproduzierbarkeit kann für die Fehlersuche bei Monte-Carlo-Simulationen genutzt werden, da man dasselbe Ergebnis erhält, wenn man eine Simulation mehrmals hintereinander mit demselben Seed durchführt, was es einfacher macht, Änderungen an anderen Stellen des Modells zu erkennen. Da sie keine natürliche Entropiequelle benötigen, die nur eine endliche Menge an Entropie in der Umgebung in einer endlichen Zeit ernten kann, ist es weniger wahrscheinlich, dass Pseudozufallszahlen die erforderliche Simulationszeit erhöhen als echte Zufallszahlen.
Im Gegenzug für die Bequemlichkeit von Pseudozufallszahlen müssen einige zusätzliche Vorsichtsmaßnahmen getroffen werden. Die Pseudozufallszahl ist für verschiedene Werte des Seeds unterschiedlich, aber derselbe Seed wird wiederholt dieselbe Zahl erzeugen. Um dies in einem COMSOL-Modell zu sehen, erstellen Sie einen Knoten Global Evaluation und werten die eingebaute Funktion random wiederholt mit einem konstanten Wert aus, z.B. random(1). Die Ausgabe steht in keinem offensichtlichen Zusammenhang mit der Zahl 1 (in diesem Sinne erscheint sie also “zufällig”), aber der Wert bleibt gleich, wenn der Ausdruck mehrfach ausgewertet wird (und somit erscheint die Verteilung der Werte nicht zufällig). Dies wird unten veranschaulicht.
Wenn bei jeder Auswertung der Zufallszahl ein anderer Seed verwendet wird, erhalten Sie bei jeder Auswertung der Zufallszahl ein anderes Ergebnis. Sehen Sie sich die Tabelle im folgenden Screenshot an, in der die Zeit als Eingabeargument für die Zufallsfunktion verwendet wird, und vergleichen Sie sie mit der vorherigen Auswertung.
Monte-Carlo-Simulationen von Teilchensystemen beinhalten oft große Gruppen von Teilchen, die mit zufälligen Anfangsbedingungen freigesetzt werden und zufälligen Kräften ausgesetzt sind. Einige Beispiele für Zufallsphänomene, an denen Gruppen von Teilchen beteiligt sind, sind:
- Bei der Freisetzung von Ionen- und Elektronenstrahlen wird die Anfangsposition jedes Ions im Phasenraum aus einer Verteilung abgetastet – ein Schwerpunkt der nachfolgenden Blog-Beiträge in dieser Serie
- Neutralisierung von Ionen durch zufällige Ladungsaustauschkollisionen mit einem verdünnten Hintergrundgas
- Turbulente Dispersion von Teilchen in einer Fluidströmung mit hoher Reynolds-Zahl
- Modellierung der Partikeldiffusion mit einer Brownschen Kraft
Wenn jedes Teilchen die gleichen pseudozufälligen Zahlen erhält, ist die Simulation natürlich völlig unphysikalisch. Im Falle von Ionen, die mit einem Hintergrundgas interagieren, würde zum Beispiel jedes Ion zu exakt denselben Zeiten wie alle anderen Ionen mit den Gasmolekülen oder Atomen kollidieren. Um dies zu verhindern, müssen alle Zufallszahlen, die an der Teilchensimulation beteiligt sind, mit Seeds versehen werden, die für jedes Teilchen einzigartig sind.
Ein Ansatz ist die Verwendung des Teilchenindex, einer Ganzzahl, die für jedes Teilchen einzigartig ist, als Teil des Seeds. Die Variable für den Teilchenindex lautet <scope>.pidx, wobei <scope> ein eindeutiger Bezeichner für die Instanz des Physik-Interfaces ist. Für das Mathematical Particle Tracing Interface lautet der Teilchenindex normalerweise pt.pidx. Die Funktion random(pt.pidx) liefert für jedes Teilchen eine andere Pseudozufallszahl.
Eine weitere Komplikation ergibt sich, wenn die Teilchen während ihrer gesamten Lebensdauer zufälligen Kräften ausgesetzt sind. Wenn beispielsweise eine Zufallszahl verwendet wird, um zu bestimmen, ob es zu einer Kollision mit einem Gasmolekül kommt, möchten Sie nicht zu jedem Zeitpunkt dieselbe Zufallszahl für ein bestimmtes Teilchen verwenden – dann könnte das Teilchen nur bei jedem einzelnen Zeitschritt eine Kollision erleiden oder überhaupt nicht! Die Lösung besteht darin, einen Zufallszahlen-Seed zu definieren, der mehrere Argumente verwendet: mindestens ein Argument, das sich von den Teilchen unterscheidet, und eines, das sich von den verschiedenen simulierten Zeiten unterscheidet. Zusätzliche Argumente können erforderlich sein, wenn die Simulation mehrere Pseudozufallszahlen erfordert, die unabhängig voneinander gesampelt werden müssen. Eine typische Verwendung der Zufallsfunktion könnte dann eine Form wie zufällig(pt.pidx,t,1) annehmen, wobei das letzte Argument 1 durch andere numerische Werte ersetzt werden kann, wenn zusätzliche unabhängige Pseudozufallszahlen benötigt werden.
Ergebnisse: Die Rayleigh-Verteilung
Kehren wir zu dem ursprünglichen Problem der Stichprobenziehung aus der Rayleigh-Verteilung zurück. Nehmen wir an, wir haben eine Teilchenpopulation und wollen eine Stichprobe pro Teilchen ziehen, so dass die resultierenden Werte der Rayleigh-Verteilung folgen. In diesem Beispiel verwenden wir Gleichung (2) mit σ = 3. Definieren Sie in einem COMSOL-Modell die folgenden Variablen:
| Name | Ausdruck | Beschreibung |
|---|---|---|
rn
|
0.5+random(pt.pidx)
|
Zufälliges Argument
|
sigma
|
3
|
Skalierungsparameter
|
val
|
sigma*sqrt(-2*log(rn))
|
Aus der Raleigh-Verteilung gezogener Wert
|
Beachten Sie, dass die letzte Zeile nur Gleichung (3) ist. Die folgende Darstellung ist ein Histogramm des Wertes von rn für eine Population von 1000 Teilchen. Die glatte Kurve ist die exakte Rayleigh-Verteilung, die mit einer Analytic Funktion definiert wurde.
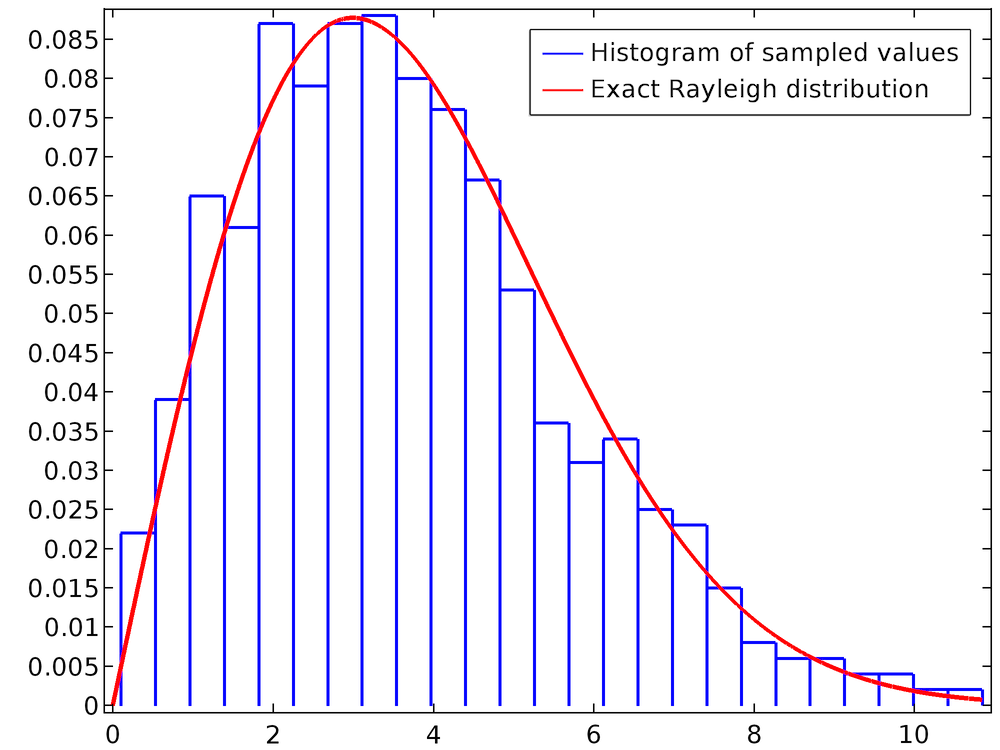
Bei Kurven mit vielen feinen Details kann eine größere Anzahl von Teilchen erforderlich sein, um die WVF genau zu erfassen.
Ein Hinweis zu Interpolationsfunktionen
Wenn eine WVF in COMSOL Multiphysics® als Interpolation Funktion anstelle einer Analytic oder Piecewise Funktion eingegeben wird, können Sie integrierte Funktionen verwenden, um automatisch eine Zufallsfunktion zu definieren, die eine Stichprobe aus der angegebenen WVF zieht.
Angenommen, wir haben eine Interpolationsfunktion, die linear zwischen den folgenden Datenpunkten interpoliert:
| x | f(x) |
|---|---|
| 0 | 0 |
| 0.2 | 0.6 |
| 0.4 | 0.7 |
| 0.6 | 1.2 |
| 0.8 | 1.2 |
| 1 | 0 |
Der folgende Screenshot zeigt, wie diese Daten in die Interpolationsfunktion eingegeben werden können. Wenn Sie das Kontrollkästchen Define random function im Einstellungsfenster für die Funktion Interpolation aktivieren, können Sie automatisch eine Funktion rn_int1 definieren, die aus dieser Verteilung Stichproben zieht. Im Grafikfenster zeigt das Histogramm eine Zufallsstichprobe von 1000 Datenpunkten, und die kontinuierliche Kurve ist die Interpolationsfunktion selbst. Die zusätzlichen Faktoren 20 und 0,74 werden zur Korrektur der Anzahl der Bins bzw. zur Normalisierung der Interpolationsfunktion verwendet.
Die Stärke von Wahrscheinlichkeitsverteilungsfunktionen
Bis jetzt haben wir gesehen, wie Wahrscheinlichkeitsverteilungsfunktionen, kumulative Verteilungsfunktionen und ihre Inversen zusammenhängen. Wir haben auch verschiedene Techniken für die Stichprobenziehung aus gleichmäßigen und ungleichmäßigen WVF in COMSOL-Modellen besprochen. Im nächsten Beitrag unserer Serie über Phasenraumverteilungen in der Strahlphysik werden wir die Physik von Ionen- und Elektronenstrahlen erläutern und zeigen, wie wichtig das Verständnis von WVF für die genaue Modellierung von Strahlsystemen ist.
Weitere Beiträge in dieser Serie
- Phasenraumverteilungen und Emissionsvermögen in 2D-Strahlen geladener Teilchen (Teil 2)
- Ziehen aus Phasenraumverteilungen in 3D-Strahlen geladener Teilchen (Teil 3)
Referenzen
- Humphries, Stanley. Charged particle beams. Courier Corporation, 2013.
- Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.







Kommentare (0)