Welches Turbulenzmodell wähle ich für meine CFD-Anwendung?

Die COMSOL Multiphysics^®-Software bietet verschiedene Formulierungen für die Lösung turbulenter Strömungsprobleme: das L-VEL-, das algebraische yPlus-, das Spalart-Allmaras-, das k-ε-, das k-ω-, das k-ε-Modell mit niedriger Reynolds-Zahl, das SST- und das v2-f-Turbulenzmodell. Diese Formulierungen sind im CFD Module verfügbar, und die Modelle L-VEL, algebraisches yPlus, k-ε und k-ε mit niedrige Reynolds-Zahl sind auch im Heat Transfer Module verfügbar. In diesem Blog-Beitrag erfahren Sie, warum Sie diese verschiedenen Turbulenzmodelle verwenden, wie Sie zwischen ihnen wählen und wie Sie sie effizient einsetzen können.

Dieser Beitrag wurde ursprünglich im Jahr 2013 veröffentlicht. Er wurde inzwischen aktualisiert und enthält nun alle Turbulenzmodelle, die derzeit mit dem CFD Module ab Version 5.3 der COMSOL^®-Software verfügbar sind.

Einführung in die Modellierung von Turbulenz

Betrachten wir zunächst die Fluidströmung über eine flache Platte, wie in der Abbildung unten dargestellt. Das gleichmäßige Geschwindigkeitsprofil trifft auf die Vorderkante der flachen Platte, und eine laminare Randschicht beginnt sich zu entwickeln. Die Strömung in diesem Bereich ist sehr vorhersehbar. Nach einer gewissen Entfernung beginnen sich in der Randschicht kleine chaotische Oszillationen zu entwickeln und die Strömung geht langsam in Turbulenz über und wird schließlich vollständig turbulent.

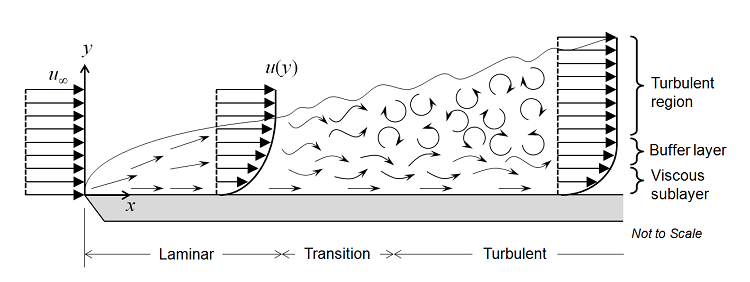
Der Übergang zwischen diesen drei Regionen lässt sich mithilfe der Reynolds-Zahl definieren, Re=\rho v L/\mu, wobei \rho die Fluiddichte, v die Geschwindigkeit, L die charakteristische Länge (in diesem Fall der Abstand von der Vorderkante), und \mu die dynamische Viskosität des Fluids ist. Wir gehen davon aus, dass es sich um ein Newtonsches Fluid handelt, was bedeutet, dass die viskose Spannung direkt proportional zur Schergeschwindigkeit ist, mit der dynamischen Viskosität als Proportionalitätskonstante. Dies gilt in guter Näherung für eine Vielzahl von Fluiden in technischen Anwendungen, wie z.B. für Luft oder Wasser. Die Dichte kann in Abhängigkeit vom Druck variieren, obwohl hier davon ausgegangen wird, dass das Fluid nur schwach kompressibel ist, was bedeutet, dass die Mach-Zahl weniger als etwa 0,3 beträgt. Die Option für schwach kompressible Strömung in den Strömungs-Interfaces in COMSOL Multiphysics^® vernachlässigt den Einfluss von Druckwellen auf die Strömungs- und Druckfelder.

Im laminaren Regime kann die Fluidströmung vollständig vorhergesagt werden, indem die Navier-Stokes-Gleichungen gelöst werden, die die Geschwindigkeits- und Druckfelder liefern. Gehen wir zunächst davon aus, dass sich das Geschwindigkeitsfeld nicht mit der Zeit ändert. Ein Beispiel dafür finden Sie im Modell der Blasius-Randschicht. Wenn die Strömung beginnt, in Turbulenz überzugehen, kommt es zu Oszillationen in der Strömung, obwohl sich der Einlassdurchfluss nicht mit der Zeit ändert. Es ist dann nicht mehr möglich, anzunehmen, dass die Strömung zeitlich unveränderlich ist. In diesem Fall ist es notwendig, die zeitabhängigen Navier-Stokes-Gleichungen zu lösen, und das verwendete Netz muss fein genug sein, um die Größe der kleinsten Wirbel in der Strömung aufzulösen. Eine solche Situation wird in dem Lehrmodell Strömung an einem Zylinder demonstriert. Beachten Sie, dass die Strömung in diesem Modell zwar instationär, aber dennoch laminar ist. Stationäre und zeitabhängige laminare Strömungsprobleme erfordern keine Zusatzmodule und können mit COMSOL Multiphysics^® alleine gelöst werden.

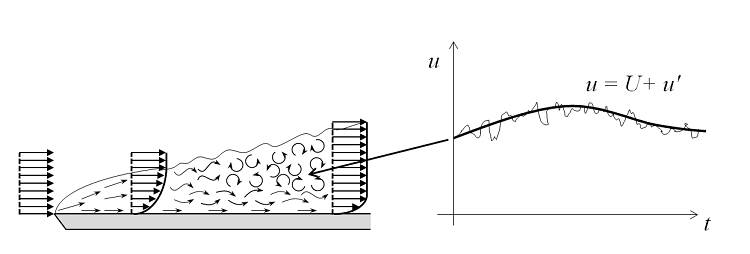
Wenn die Strömungsgeschwindigkeit – und damit auch die Reynolds-Zahl – zunimmt, weist das Strömungsfeld kleine Wirbel auf und die räumlichen und zeitlichen Skalen der Oszillationen werden so klein, dass es rechnerisch nicht mehr möglich ist, sie mit den Navier-Stokes-Gleichungen zu lösen, zumindest in den meisten praktischen Fällen. In diesem Strömungsregime können wir eine Reynolds-gemittelte Navier-Stokes-Formulierung (RANS) verwenden, die auf der Beobachtung beruht, dass das Strömungsfeld (u) im Laufe der Zeit kleine, lokale Oszillationen (u’) enthält und in einem zeitlich gemittelten Sinn (U) behandelt werden kann. Für Ein- und Zweigleichungsmodelle werden zusätzliche Transportgleichungen für Turbulenzvariablen eingeführt, wie z.B. die kinetische Energie der Turbulenz (k in k-ε und k-ω).

Bei algebraischen Modellen werden zur Beschreibung der Turbulenzintensität algebraische Gleichungen eingeführt, die vom Geschwindigkeitsfeld – und in einigen Fällen auch vom Abstand zu den Wänden – abhängen. Aus den Abschätzungen für die Turbulenzvariablen wird eine Wirbelviskosität berechnet, die zur molekularen Viskosität des Fluids hinzukommt. Der Impuls, der von den kleinen Wirbeln übertragen werden würde, wird stattdessen in einen viskosen Transport umgewandelt. Die Turbulenzdissipation dominiert in der Regel überall gegenüber der viskosen Dissipation, außer in der viskosen Schicht in der Nähe von festen Wänden. Hier muss das Turbulenzmodell den Turbulenzgrad kontinuierlich reduzieren, wie zum Beispiel bei Modellen mit niedriger Reynolds-Zahl. Oder es müssen neue Randbedingungen mit Hilfe von Wandfunktionen berechnet werden.

Modelle mit niedriger Reynolds-Zahl

Der Begriff “Modell mit niedriger Reynolds-Zahl” klingt wie ein Widerspruch, da Strömungen ja gerade dann turbulent sind, wenn die Reynolds-Zahl hoch ist. Die Bezeichnung “niedrige Reynolds-Zahl” bezieht sich nicht auf die Strömung auf globaler Ebene, sondern auf den wandnahen Bereich, in dem viskose Effekte dominieren, d.h. auf die viskose Unterschicht in der obigen Abbildung. Ein Modell mit niedriger Reynolds-Zahl ist ein Modell, das das begrenzende Verhalten verschiedener Strömungsgrößen korrekt wiedergibt, wenn der Abstand zur Wand gegen Null geht. So muss ein Modell mit niedriger Reynolds-Zahl z.B. vorhersagen, dass k~y² wenn y→0. Ein korrektes Grenzverhalten bedeutet, dass das Turbulenzmodell zur Modellierung der gesamten Randschicht verwendet werden kann, einschließlich der viskosen Unterschicht und der Pufferschicht.

Die meisten ω-basierten Modelle sind von Haus aus Modelle mit niedriger Reynolds-Zahl. Aber das Standard k-ε-Modell und andere häufig anzutreffende k-ε-Modelle sind keine Modelle mit niedriger Reynolds-Zahl. Einige von ihnen können jedoch mit sogenannten Dämpfungsfunktionen ergänzt werden, die das richtige Grenzverhalten ergeben. Sie werden dann als k-ε-Modelle mit niedriger Reynolds-Zahl bezeichnet.

Modelle mit niedriger Reynolds-Zahl liefern oft eine sehr genaue Beschreibung der Randschicht. Die scharfen Gradienten in Wandnähe erfordern jedoch eine sehr hohe Netzauflösung, was wiederum bedeutet, dass die hohe Genauigkeit mit hohen Rechenkosten verbunden ist. Aus diesem Grund werden für industrielle Anwendungen oft alternative Methoden zur Modellierung der Strömung in Wandnähe eingesetzt.

Wandfunktionen

Die turbulente Strömung in der Nähe einer flachen Wand kann in vier Bereiche unterteilt werden. An der Wand ist die Strömungsgeschwindigkeit gleich Null, und in einer dünnen Schicht darüber wächst sie linear mit dem Abstand zur Wand. Dieser Bereich wird als viskose Unterschicht oder laminare Unterschicht bezeichnet. Weiter von der Wand entfernt befindet sich eine Region, die Pufferschicht genannt wird. In der Pufferregion beginnen die Turbulenzspannungen gegenüber den viskosen Spannungen zu dominieren und sie geht schließlich in eine Region über, in der die Strömung vollständig turbulent ist und die durchschnittliche Strömungsgeschwindigkeit mit dem Logarithmus des Abstands zur Wand wächst. Dies wird als Log-law-Region bezeichnet. Noch weiter von der Wand entfernt, geht die Strömung in den Freistrombereich über. Die viskose und die Pufferschicht sind sehr dünn und wenn der Abstand zum Ende der Pufferschicht \delta beträgt, dann erstreckt sich die logarithmische Region etwa 100\delta von der Wand.

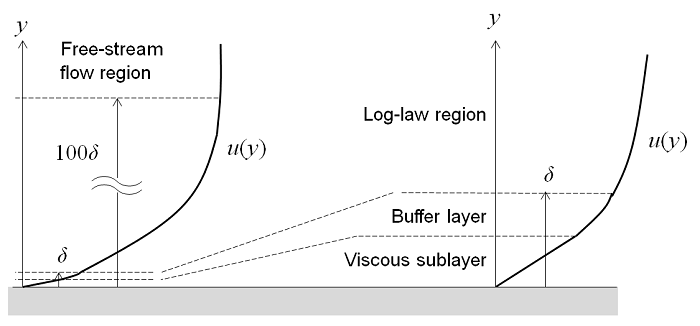
Das Strömungsfeld in allen vier dieser Regionen kann mit einem RANS-Modell berechnet werden. Da die Dicke der Pufferschicht jedoch so gering ist, kann es von Vorteil sein, in dieser Region eine Näherung zu verwenden. Wandfunktionen ignorieren das Strömungsfeld in der Pufferregion und berechnen analytisch eine Fluidgeschwindigkeit ungleich Null an der Wand. Wenn Sie eine Wandfunktion-Formulierung verwenden, gehen Sie von einer analytischen Lösung für die Strömung in der viskosen Schicht aus und die daraus resultierenden Modelle haben einen deutlich geringeren Rechenaufwand. Dies ist ein sehr nützlicher Ansatz für viele praktische technische Anwendungen.

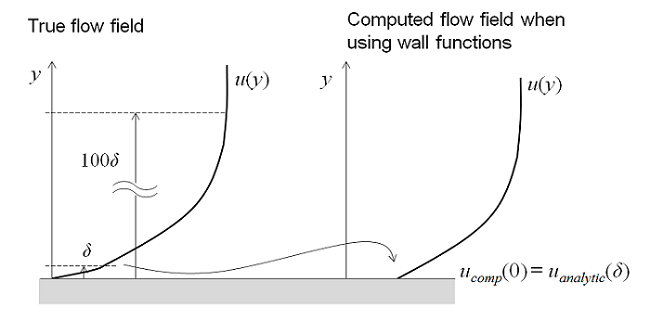
Wenn Sie einen Genauigkeitsgrad benötigen, der über das hinausgeht, was die Wandfunktion-Formulierungen bieten, dann sollten Sie ein Turbulenzmodell in Betracht ziehen, das das gesamte Strömungsregime löst, wie oben für die Modelle mit niedriger Reynolds-Zahl beschrieben. Zum Beispiel möchten Sie vielleicht den Auftrieb und Strömungswiderstand eines Objekts oder den Wärmetransport zwischen dem Fluid und der Wand berechnen.

Automatische Behandlung der Wand

Die automatische Wandbehandlungsfunktion, die seit COMSOL Multiphysics^® Version 5.3 verfügbar ist, kombiniert die Vorteile von Wandfunktionen und Modellen mit niedriger Reynolds-Zahl. Die automatische Wandbehandlung passt die Formulierung an das im Modell verfügbare Netz an, so dass Sie sowohl Robustheit als auch Genauigkeit erhalten. Bei einem groben Randschichtnetz verwendet die Funktion zum Beispiel eine robuste Wandfunktion-Formulierung. Bei einem dichten Randschichtnetz hingegen verwendet die automatische Wandbehandlung eine Formulierung mit niedriger Reynolds-Zahl, um das Geschwindigkeitsprofil vollständig an der Wand aufzulösen.

Der Übergang von einer Formulierung mit niedriger Reynolds-Zahl zu einer Wandfunktion-Formulierung ist fließend. Die Software mischt die beiden Formeln in den Randelementen. Dann berechnet die Software den Wandabstand der Gitterpunkte der Randelemente (dies geschieht in viskosen Einheiten, die durch einen liftoff gegeben sind). Die kombinierten Formulierungen werden dann für die Randbedingungen verwendet.

Alle Turbulenzmodelle in COMSOL Multiphysics^®, mit Ausnahme des k-ε-Modells, unterstützen die automatische Wandbehandlung. Das bedeutet, dass die Modelle mit niedriger Reynolds-Zahl für industrielle Anwendungen verwendet werden können und dass die Fähigkeit zur Modellierung niedriger Reynolds-Zahlen nur dann eingesetzt wird, wenn das Netz fein genug ist.

Über die verschiedenen Turbulenzmodelle

Die acht RANS-Turbulenzmodelle unterscheiden sich in der Art und Weise, wie sie die Strömung in der Nähe von Wänden modellieren, in der Anzahl der zusätzlichen Variablen, für die eine Lösung gefunden wird, und darin, was diese Variablen darstellen. Alle diese Modelle erweitern die Navier-Stokes-Gleichungen um einen zusätzlichen Turbulenz-Wirbelviskositätsterm, aber sie unterscheiden sich darin, wie dieser berechnet wird.

L-VEL und yPlus

Die L-VEL und algebraischen yPlus-Turbulenzmodelle berechnen die Wirbelviskosität mit algebraischen Ausdrücken, die nur auf der lokalen Fluidgeschwindigkeit und dem Abstand zur nächstgelegenen Wand basieren. Sie lösen keine zusätzlichen Transportgleichungen. Diese Modelle lösen die Strömung überall und sind die robustesten und am wenigsten rechenintensiven der acht Turbulenzmodelle. Obwohl sie im Allgemeinen die ungenauesten Modelle sind, liefern sie gute Näherungen für interne Strömungen, insbesondere bei elektronischen Kühlanwendungen.

Spalart-Allmaras

Das Spalart-Allmaras-Modell fügt eine einzige zusätzliche Variable für eine ungedämpfte kinematische Wirbelviskosität hinzu. Es ist ein Modell mit niedriger Reynolds-Zahl und kann das gesamte Strömungsfeld bis hin zur festen Wand auflösen. Das Modell wurde ursprünglich für aerodynamische Anwendungen entwickelt und hat den Vorteil, dass es relativ robust ist und moderate Auflösungsanforderungen hat. Die Erfahrung zeigt, dass dieses Modell Felder, die Scherströmungen, getrennte Strömungen oder abklingende Turbulenzen aufweisen, nicht genau berechnen kann. Sein Vorteil ist, dass es relativ stabil ist und eine gute Konvergenz aufweist.

k-ε

Das k-ε-Modell löst zwei Variablen: k, die kinetische Energie der Turbulenz, und ε (Epsilon), die Dissipationsrate der kinetischen Energie der Turbulenz. In diesem Modell werden Wandfunktionen verwendet, so dass die Strömung in der Pufferregion nicht simuliert wird. Das k-ε-Modell war in der Vergangenheit aufgrund seiner guten Konvergenzrate und seines relativ geringen Speicherbedarfs sehr beliebt für industrielle Anwendungen. Es berechnet Strömungsfelder, die starke Druckgradienten und Krümmungen der Strömung oder Strahlströmungen aufweisen, nicht sehr genau. Bei externen Strömungsproblemen um komplexe Geometrien herum ist es jedoch gut geeignet. So kann das k-ε-Modell beispielsweise zur Lösung der Luftströmung über einen Ahmed-Körper verwendet werden.

Die unten aufgeführten Turbulenzmodelle sind alle nichtlinearer als das k-ε-Modell und es kann oft schwierig sein, sie zu konvergieren, wenn man keine gute Anfangsschätzung hat. Das k-ε Modell kann verwendet werden, um eine gute Anfangsschätzung zu liefern. Lösen Sie das Modell einfach mit dem k-ε-Modell und verwenden Sie dann die neue Funktion Generate New Turbulence Interface, die im CFD Module mit COMSOL Multiphysics^® Version 5.3 verfügbar ist.

k-ω

Das k-ω-Modell ähnelt dem k-ε-Modell, aber es löst ω (omega) – die spezifische Dissipationsrate der kinetischen Energie. Es ist ein Modell für niedrige Reynolds-Zahlen, aber es kann auch in Verbindung mit Wandfunktionen verwendet werden. Es ist nichtlinearer und daher schwieriger zu konvergieren als das k-ε-Modell und es reagiert sehr empfindlich auf die anfängliche Schätzung der Lösung. Das k-ω-Modell ist in vielen Fällen nützlich, in denen das k-ε-Modell nicht genau ist, z.B. bei internen Strömungen, Strömungen mit starker Krümmung, getrennten Strömungen und Jets. Ein gutes Beispiel für eine interne Strömung ist die Strömung durch eine Rohrbiegung.

k-ε mit niedriger Reynolds-Zahl

Das k-ε-Modell mit niedriger Reynolds-Zahl ähnelt dem k-ε-Modell, benötigt aber keine Wandfunktionen: Es kann die Strömung überall lösen. Es ist eine logische Erweiterung des k-ε-Modells und hat viele seiner Vorteile, erfordert aber im Allgemeinen ein dichteres Netz; nicht nur an den Wänden, sondern überall dort, wo die Eigenschaften der niedrigen Reynolds-Zahl zum Tragen kommen und die Turbulenz dämpfen. Manchmal kann es sinnvoll sein, das k-ε-Modell zu verwenden, um zunächst eine gute Anfangsbedingung für die Lösung des k-ε-Modells mit niedriger Reynolds-Zahl zu berechnen. Eine andere Möglichkeit ist, die automatische Wandbehandlung zu verwenden und mit einem groben Randschichtnetz zu beginnen, um Wandfunktionen zu erhalten und dann die Randschicht an den interessanten Wänden zu verfeinern, um Modelle mit niedriger Reynolds-Zahl zu erhalten.

Das k-ε-Modell mit niedriger Reynolds-Zahl kann Auftriebs- und Strömungswiderstandskräfte berechnen und die Wärmeströme können im Vergleich zum k-ε-Modell mit höherer Genauigkeit modelliert werden. Es hat sich auch gezeigt, dass es die Abtrennung und Wiederanbindung für eine Reihe von Fällen durchaus gut vorhersagen kann.

SST

Das SST-Modell ist eine Kombination aus dem k-ε-Modell in der freien Strömung und dem k-ω-Modell in Wandnähe. Es ist ein Modell für niedrige Reynolds-Zahlen und sozusagen das “Go-to”-Modell für industrielle Anwendungen. Es hat ähnliche Auflösungsanforderungen wie das k-ω-Modell und das k-ε-Modell für niedrige Reynolds-Zahlen, aber seine Formulierung beseitigt einige Schwächen, die die reinen k-ω- und k-ε-Modelle aufweisen. In einem Tutorial-Modellbeispiel löst das SST-Modell die Strömung über ein NACA-0012-Tragflächenprofil. Die Ergebnisse sind gut mit experimentellen Daten vergleichbar.

v2-f

In der Nähe von Wandrändern sind die Schwankungen der Geschwindigkeit in den Richtungen parallel zur Wand in der Regel viel größer als in der Richtung senkrecht zur Wand. Die Geschwindigkeitsschwankungen werden als anisotrop bezeichnet. Weiter von der Wand entfernt sind die Schwankungen in allen Richtungen gleich groß. Die Geschwindigkeitsschwankungen werden isotrop.

Das v2-f-Turbulenzmodell beschreibt die Anisotropie der Turbulenzintensität in der turbulenten Randschicht mit zwei neuen Gleichungen, zusätzlich zu den beiden Gleichungen für die kinetische Turbulenzenergie (k) und die Dissipationsrate (ε). Die erste Gleichung beschreibt den Transport von turbulenten Geschwindigkeitsschwankungen normal zu den Stromlinien. Die zweite Gleichung berücksichtigt nichtlokale Effekte wie die wandbedingte Dämpfung der Umverteilung der kinetischen Energie der Turbulenz zwischen der normalen und der parallelen Richtung.

Sie sollten dieses Modell für geschlossene Strömungen über gekrümmten Oberflächen verwenden, zum Beispiel um Wirbelstürme zu modellieren.

Überlegungen zur Vernetzung bei CFD-Problemen

Die Lösung von Strömungsproblemen jeglicher Art – laminar oder turbulent – ist rechenintensiv. Es sind relativ feine Netze erforderlich und es gibt viele Variablen, für die eine Lösung gefunden werden muss. Im Idealfall verfügen Sie über einen sehr schnellen Computer mit vielen Gigabyte Arbeitsspeicher, um solche Probleme zu lösen, aber die Lösungszeiten können bei größeren 3D-Modellen trotzdem Stunden oder Tage betragen. Daher möchten wir ein möglichst einfaches Netz verwenden, das dennoch alle Details der Strömung erfasst.

Wenn wir auf die Abbildung am Anfang dieses Blog-Beitrags zurückblicken, stellen wir fest, dass sich das Geschwindigkeitsfeld bei der flachen Platte (und bei den meisten Strömungsproblemen) in der tangentialen Richtung zur Wand recht langsam, in der normalen Richtung jedoch recht schnell ändert, insbesondere wenn wir die Pufferschichtregion betrachten. Diese Beobachtung motiviert die Verwendung eines Randschichtnetzes. Bei Randschichtnetzen (die bei unserer physikbasierten Vernetzung standardmäßig für Wände verwendet werden) werden dünne Rechtecke in 2D oder dreieckige Prismen in 3D an den Wänden eingefügt. Diese Elemente mit hohem Seitenverhältnis lösen die Variationen der Strömungsgeschwindigkeit senkrecht zum Rand gut auf und reduzieren gleichzeitig die Anzahl der Berechnungspunkte in tangentialer Richtung zum Rand.

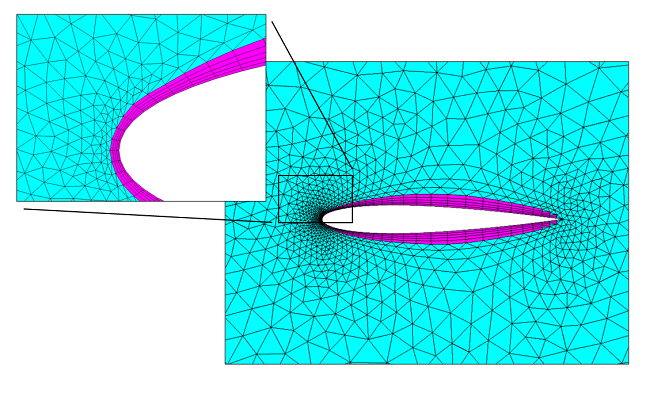
Das Randschichtnetz (magenta) um ein Tragflächenprofil und das umgebende Dreiecksnetz (blau) für ein 2D-Netz.

Das Randschichtnetz (magenta) um einen stumpfen Körper und das umgebende tetraedrische Netz (blau) für ein volumetrisches 3D-Netz.

Auswertung der Ergebnisse Ihres Turbulenzmodells

Sobald Sie eines dieser Turbulenzmodelle zur Lösung Ihrer Strömungssimulation verwendet haben, werden Sie überprüfen wollen, ob die Lösung korrekt ist. Wie bei jedem Finite-Elemente-Modell können Sie das Modell einfach mit immer feineren Gittern ausführen und beobachten, wie sich die Lösung mit zunehmender Netzverfeinerung verändert. Sobald sich die Lösung nicht mehr innerhalb eines für Sie akzeptablen Wertes verändert, kann Ihre Simulation in Bezug auf das Netz als konvergiert betrachtet werden. Es gibt jedoch noch weitere Werte, die Sie bei der Modellierung von Turbulenzen überprüfen müssen.

Bei der Verwendung von Wandfunktion-Formulierungen sollten Sie die wall resolution viscous units überprüfen (dieser Plot wird standardmäßig erzeugt). Dieser Wert gibt an, wie weit in die Randschicht hinein Ihr Berechnungsgebiet beginnt, und sollte nicht zu groß sein. Sie sollten in Erwägung ziehen, Ihr Netz in Richtung der Wandnormalen zu verfeinern, wenn es Regionen gibt, in denen die Wandauflösung mehrere hundert Einheiten überschreitet. Die zweite Variable, die Sie bei der Verwendung von Wandfunktionen überprüfen sollten, ist der wall liftoff (in Längeneinheiten). Diese Variable hängt mit der angenommenen Dicke der viskosen Schicht zusammen und sollte im Verhältnis zu den umgebenden Abmessungen der Geometrie klein sein. Wenn dies nicht der Fall ist, sollten Sie das Netz auch in diesen Regionen verfeinern.

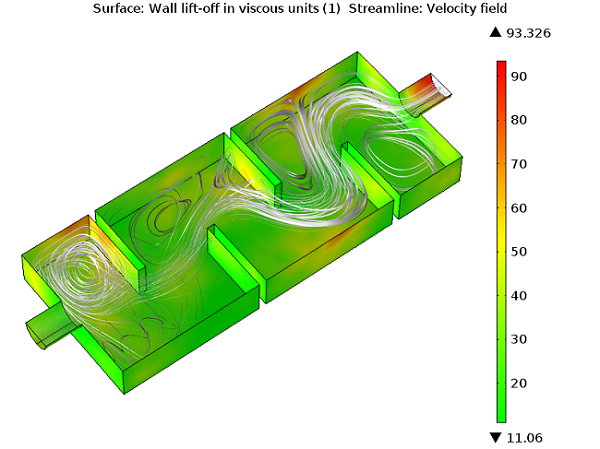
Der maximale wall liftoff in viskosen Einheiten ist kleiner als 100, so dass es nicht notwendig ist, das Randschichtnetz zu verfeinern.

Wenn Sie ein Modell mit einer Wandbehandlung für niedrige Reynolds-Zahlen lösen, überprüfen Sie den dimensionless distance to cell center (ebenfalls standardmäßig erzeugt). Dieser Wert sollte bei den algebraischen Modellen überall in der Größenordnung von Eins liegen und bei allen Zweigleichungsmodellen und dem v2-f-Modell kleiner als 0,5 sein. Wenn dies nicht der Fall ist, müssen Sie das Netz in diesen Regionen verfeinern.

Abschließende Gedanken

In diesem Blog-Beitrag haben wir die verschiedenen in COMSOL Multiphysics^® verfügbaren Turbulenzmodelle besprochen und aufgezeigt, wann und warum Sie jedes einzelne davon verwenden sollten. Die wahre Stärke der COMSOL^®-Software liegt darin, dass Sie Ihre Strömungssimulationen mit anderen physikalischen Modellen kombinieren können, z.B. zur Ermittlung von Spannungen auf einem Solarkollektor bei starkem Wind, zur Modellierung der erzwungenen Konvektion in einem Wärmetauscher oder zum Stofftransport in einem Mischer, um nur einige Möglichkeiten zu nennen.

Wenn Sie daran interessiert sind, die COMSOL^®-Software für Ihre CFD- und Multiphysik-Simulationen zu verwenden, oder wenn Sie eine Frage haben, die hier nicht angesprochen wurde, kontaktieren Sie uns.