Perfectly Matched Layers und Streuungs-Randbedingungen für Probleme der Wellen-Elektromagnetik

Bei der Lösung von Problemen aus der Wellen-Elektromagnetik ist es wahrscheinlich, dass Sie einen Bereich mit offenen Rändern modellieren wollen – d.h. einen Rand des Berechnungsbereichs, durch den eine elektromagnetische Welle ohne jegliche Reflexion hindurchgehen kann. COMSOL Multiphysics bietet hierfür mehrere Lösungen an. Heute werden wir uns die Verwendung von Streuungsrandbedingungen und Perfectly Matched Layers für das Abschneiden von Bereichen ansehen und die jeweiligen Vorteile besprechen.

Warum wollen wir einen Bereich abschneiden?

Wir sind oft an der Modellierung eines strahlenden Objekts, wie etwa einer Antenne, im freien Raum interessiert. Wir können dieses Modell erstellen, um eine Antenne auf einem Satelliten im Weltraum zu simulieren oder, was häufiger vorkommt, eine Antenne, die in einer echofreien Prüfkammer montiert ist.

Eine Antenne im unendlichen freien Raum. Wir wollen nur einen kleinen Bereich um die Antenne herum modellieren.

Solche Modelle können mithilfe der Electromagnetic Waves, Frequency Domain Formulierung im RF Module oder dem Wave Optics Module erstellt werden. Diese Module bieten ähnliche Schnittstellen zur Lösung der Frequenzbereichsform der Maxwell-Gleichungen mithilfe der Finite-Elemente-Methode. (Eine Beschreibung der wichtigsten Unterschiede zwischen diesen Modulen finden Sie in einem früheren Blog-Beitrag mit dem Titel “Computational Electromagnetics Modeling, Which Module to Use?”)

In diesem Blog-Beitrag wollen wir uns auf die Betrachtung von 2D-Problemen beschränken, bei denen sich die elektromagnetische Welle in der x-y-Ebene ausbreitet und das elektrische Feld in z-Richtung polarisiert ist. Wir werden außerdem davon ausgehen, dass unser Modellierungsbereich ein reines Vakuum ist, so dass sich die Maxwell-Gleichungen im Frequenzbereich reduzieren:

wobei E_z das elektrische Feld, die relative Permeabilität und Permittivität \mu_r = \epsilon_r = 1 im Vakuum und k_0 die Wellenzahl ist.

Die Lösung der obigen Gleichung mithilfe der Finite-Elemente-Methode erfordert einen endlichen Modellierungsbereich sowie eine Reihe von Randbedingungen. Wir wollen entlang der Außenseite Randbedingungen verwenden, die für jegliche Strahlung transparent sind. Auf diese Weise wird unser abgeschnittener Bereich eine vernünftige Annäherung an den freien Raum darstellen. Außerdem soll der abgeschnittene Bereich so klein wie möglich sein, da eine geringe Modellgröße die Rechenkosten reduziert.

Betrachten wir nun zwei der in der COMSOL Multiphysics-Simulationsumgebung verfügbaren Optionen für das Abschneiden Ihres Modellierungsbereichs: die Streuungs-Randbedingung und Perfectly Matched Layers.

Die Streuungs-Randbedingung

Eine der ersten transparenten Randbedingungen, die für wellenartige Probleme formuliert wurden, war die Sommerfeld-Strahlungsbedingung, die für 2D-Felder wie folgt beschrieben werden kann:

wobei r die radiale Achse ist.

Diese Bedingung ist genau dann nicht reflektierend, wenn die Ränder unseres Modellierungsbereichs unendlich weit von unserer Quelle entfernt sind, aber natürlich ist ein unendlich großer Modellierungsbereich unmöglich. Auch wenn wir die Sommerfeld-Bedingung nicht exakt anwenden können, so können wir doch eine vernünftige Annäherung an diese Bedingung erreichen.

Betrachten wir die Randbedingung:

Die Ähnlichkeiten zwischen dieser Bedingung und der Sommerfeld-Bedingung sind deutlich zu erkennen. Diese Randbedingung wird formell als Streuungs-Randbedingung (Scattering Boundary Condition, SBC) erster Ordnung bezeichnet und ist in COMSOL Multiphysics leicht zu implementieren. Im Grunde ist sie nichts anderes als eine Robin-Randbedingung mit einem komplexwertigen Koeffizienten.

Wenn Sie ein Beispiel für eine von Grund auf implementierte 2D-Wellengleichung mit dieser Randbedingung sehen möchten, sehen Sie sich bitte das Beispielmodell eines Beugungsmusters an.

Diese Bedingung unterliegt jedoch einer erheblichen Einschränkung. Sie ist nur dann nicht reflektierend, wenn die einfallende Strahlung genau senkrecht auf die Begrenzung auftrifft. Jede Welle, die bei nicht normalem Einfall auf den SBC trifft, wird teilweise reflektiert. Der Reflexionskoeffizient für einen ebenen Welleneinfall auf eine SBC erster Ordnung bei unterschiedlichem Einfall ist unten dargestellt.

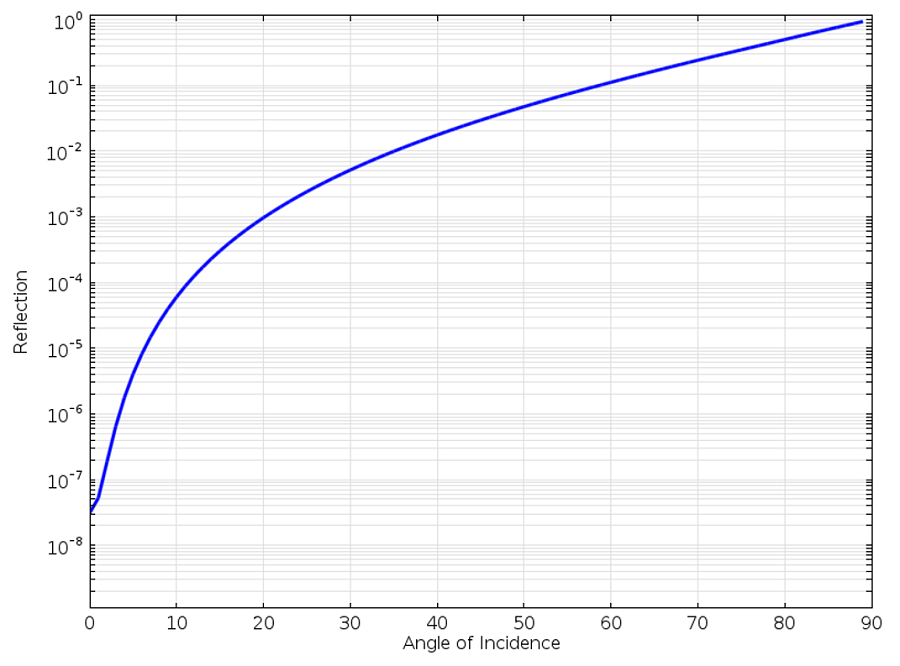
Reflexion einer ebenen Welle an der SBC erster Ordnung unter Berücksichtigung des Einfallswinkels.

Aus dem obigen Diagramm ist ersichtlich, dass die eintreffende ebene Welle bei streifendem Einfall fast vollständig reflektiert wird. Bei einem Einfallswinkel von 60° beträgt die Reflexion etwa 10 %, so dass wir gerne eine bessere Randbedingung hätten.

COMSOL Multiphysics also includes (as of version 4.4) the second-order SBC:

Diese Gleichung fügt einen zweiten Term hinzu, der die zweite tangentiale Ableitung des elektrischen Feldes entlang des Randes enthält. Auch das ist innerhalb der COMSOL-Softwarearchitektur recht einfach zu implementieren.

Vergleichen wir nun den Reflexionskoeffizienten der SBC erster und zweiter Ordnung:

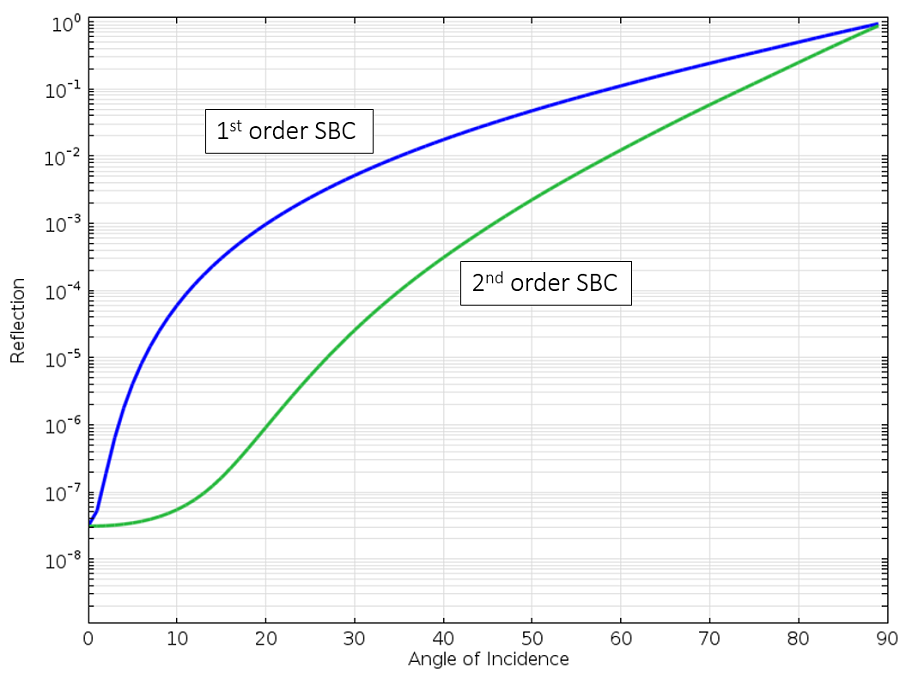
Reflexion einer ebenen Welle an der SBC erster und zweiter Ordnung unter Berücksichtigung des Einfallswinkels.

Wir sehen, dass die SBC zweiter Ordnung gleichmäßig besser ist. Wir können jetzt einen Einfallswinkel von ~75° erreichen, bevor die Reflexion 10 % beträgt. Das ist besser, aber immer noch nicht das Beste, was wir erreichen können. Wenden wir uns nun von den Randbedingungen ab und betrachten Perfectly Matched Layers.

Perfectly Matched Layers

Erinnern wir uns daran, dass wir versuchen, eine Situation wie eine Antenne in einer reflexionsarmen Testkammer zu simulieren, einem Raum mit pyramidenförmigen Keilen aus strahlungsabsorbierendem Material an den Wänden, die jedes reflektierte Signal minimieren. Dies kann unsere physikalische Analogie für den Perfectly Matched Layer (PML) sein, bei der es sich nicht um eine Randbedingung handelt, sondern um einen Bereich, den wir entlang der Außenseite des Modells hinzufügen, der alle ausgehenden Wellen absorbieren sollte.

Mathematisch gesehen ist die PML einfach ein Bereich mit einer anisotropen und komplexwertigen Permittivität und Permeabilität. Ein Beispiel für eine vollständige Ableitung dieser Tensoren finden Sie in Theorie und Berechnung elektromagnetischer Felder. Obwohl PMLs theoretisch nicht reflektierend sind, weisen sie aufgrund der numerischen Diskretisierung, d.h. des Netzes, eine gewisse Reflexion auf. Um diese Reflexion zu minimieren, wollen wir im PML ein Netz verwenden, das sich an der Anisotropie der Materialeigenschaften orientiert. Die entsprechenden PML-Netze werden im Folgenden für kreisförmige 2D- und sphärische 3D-Bereiche dargestellt. Kartesische und sphärische PMLs und ihre angemessene Verwendung werden auch in der Produktdokumentation behandelt.

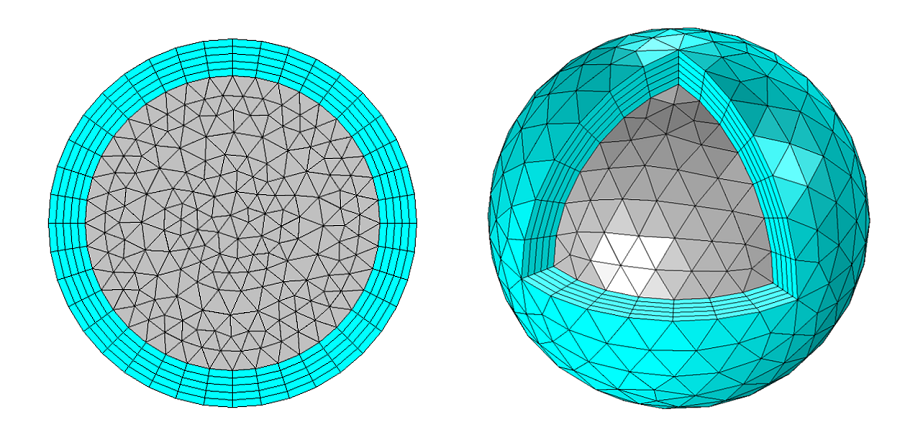
Geeignete Netze für 2D und 3D sphärische PMLs.

In COMSOL Multiphysics 5.0 können diese Netze für 3D-Probleme mithilfe der physikalisch gesteuerten Vernetzung automatisch erstellt werden, wie in diesem Video gezeigt.

Betrachten wir nun die Reflexion von einem PML unter Berücksichtigung des Einfallswinkels im Vergleich zu den SBCs:

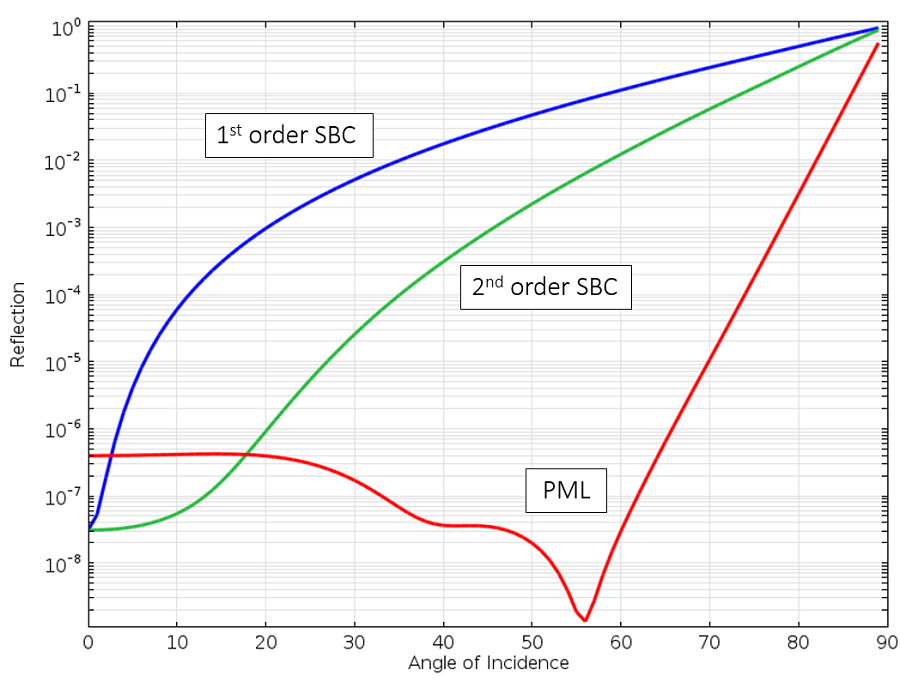
Reflexion einer ebenen Welle an der SBC erster und zweiter Ordnung und am PML unter Berücksichtigung des Einfallswinkels.

Wir sehen, dass der PML über den größten Bereich am wenigsten reflektiert. Es gibt zwar immer noch eine Reflexion, wenn sich die Welle fast genau parallel zur Grenze ausbreitet, aber solche Fälle sind in der Praxis zum Glück eher selten. Eine weitere Eigenschaft des PML, auf die wir jetzt nicht näher eingehen wollen, ist, dass er nicht nur die sich ausbreitende Welle, sondern auch jedes temporäre Feld absorbiert. Physikalisch gesehen kann man sich den PML also wirklich als ein Material mit nahezu perfekter Absorption vorstellen.

Welche Option sollten Sie also verwenden?

PML ist eindeutig der Beste der hier beschriebenen Ansätze. Allerdings benötigt PML im Vergleich zur SBC mehr Speicherplatz.

Wenn Sie sich also in einem frühen Stadium des Modellierungsprozesses befinden und ein Modell erstellen möchten, das etwas weniger rechenintensiv ist, ist die SBC zweiter Ordnung eine gute Option. Sie kann auch in Situationen verwendet werden, in denen Sie guten Grund zu der Annahme haben, dass Reflexionen an der SBC die Ergebnisse, an denen Sie interessiert sind, nicht wesentlich beeinträchtigen werden.

Aus Gründen der Kompatibilität mit früheren Versionen der Software ist die SBC erster Ordnung derzeit die Standardeinstellung, aber mit COMSOL Multiphysics Version 4.4 oder höher kann die SBC zweiter Ordnung genutzt werden. Wir haben hier nur die ebene Wellenform der SBC vorgestellt, aber zylindrische und kugelförmige (in 3D) Formen der SBC erster und zweiter Ordnung sind ebenfalls verfügbar. Sie benötigen zwar weniger Speicherplatz, weisen aber im Vergleich zum PML mehr Reflexion auf.

Die SBC und die PMLs sind geeignete Bedingungen für offene Ränder, bei denen man nicht viel über die Felder an den Rändern a priori weiß. Wenn Sie hingegen einen offenen Rand modellieren wollen, bei dem die Felder eine bestimmte Form haben, z. B. einen Rand, der einen Wellenleiter darstellt, sind die Randbedingungen Port und Lumped Port besser geeignet. Wir werden diese Bedingungen in einem der nächsten Blog-Beiträge besprechen.