Zeit als Raumdimension

Bestimmte Modellierungsprobleme können zu besonders eleganten Lösungen führen. Ein solcher Fall stellte sich kürzlich in Form der Suche nach der zeitperiodischen stationären Lösung für ein Problem mit einer nichtlinearen elektrischen Schaltung dar. Sehen wir uns diesen Fall genauer an und finden wir heraus, wie einige der Kernfunktionen der Software zu einer effizienten Umsetzung beitragen können.

Das Modellierungsszenario: Ein nichtlinearer Transformator

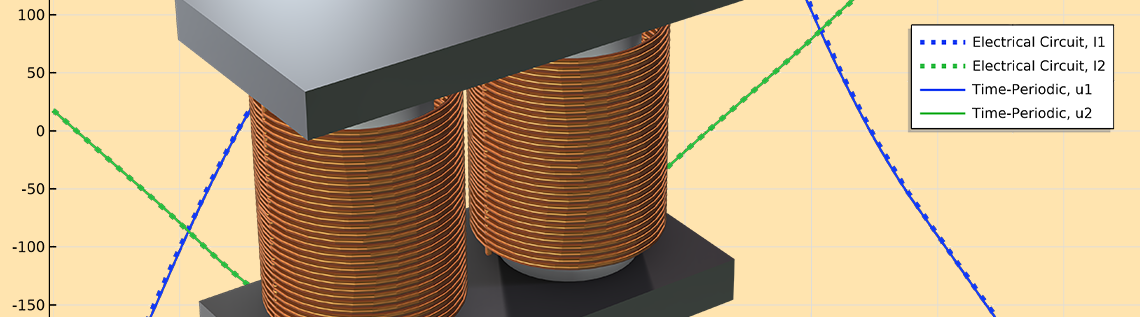
In unserem Blog-Beitrag Using Differential Inductances and the Coil Feature haben wir uns bereits mit dem Fall eines Transformators befasst, der aus zwei Spulen besteht, die um ein nichtlineares Kernmaterial gewickelt sind. Eine angelegte sinusförmige Wechselspannung induziert Ströme in der Primär- und Sekundärspule. Bei ausreichend hohen Strömen verändert die Nichtlinearität des Materials jedoch die differentiellen Induktivitäten erheblich, und die induzierten Ströme sind nicht-sinusförmig. Wir können dieses Verhalten entweder durch ein originalgetreues Modells des Geräts oder durch eine elektrischen Ersatzschaltung modellieren, in der die nichtlinearen differentiellen Induktivitäten berücksichtigt werden. Die Nichtlinearitäten führen zu Strömen, die periodisch sind, wenn auch nicht sinusförmig. Wir können diese graduelle Antwort untersuchen, indem wir ein transientes Modell für viele Perioden ausführen.

Ein Transformator, der aus zwei Spulen besteht, die um einen nichtlinearen Kern gewickelt sind. Die differentiellen Induktivitäten können aus dem Finite-Elemente-Modell extrahiert und in einem Ersatzschaltungsmodell verwendet werden.

Die Ergebnisse der Ausführung des Ersatzschaltungsmodells über viele Perioden zeigen, dass eine allmähliche Annäherung an den zeitperiodischen stationären Zustand erfolgt.

Wenn man sich die Ergebnisse ansieht, wird deutlich, dass wir für viele Perioden simulieren müssen. Wenn wir nur an der zeitperiodischen stationären Lösung interessiert sind, werden die meisten der generierten Daten nicht benötigt. Im Idealfall brauchen wir in dieser Situation eine Methode, die direkt zur zeitperiodischen Lösung führt, und damit werden wir uns hier befassen.

Umformulierung der Ersatzschaltung von Zeit zu Raum

Wenn wir uns unser Modell des elektrischen Stromkreises genauer ansehen, stellen wir fest, dass es nur zwei zeitabhängige Unbekannte gibt: I_1 und I_2, den Strom durch die Primär- und Sekundärwicklung. Betrachten wir nun nicht mehr den Schaltplan, sondern die Spannungsabfälle an den einzelnen Elementen der beiden Stromschleifen.

wobei alle differentiellen Induktivitäten Funktionen beider Ströme sind: \partial L_{ij} (I_1,I_2). Diese Gruppe gekoppelter gewöhnlicher Differentialgleichungen kann auf unzählige Arten gelöst werden. Wir beschränken uns auf den Fall, in dem die angelegte Spannung V_{AC} und die Lösung über eine Periode, T_0, zeitperiodisch ist.

Wir können sofort erkennen, dass es sich hierbei bis auf die Zeitableitungen der Ströme praktisch um eine nichtlineare algebraische Gleichung handelt. Aber was wäre, wenn wir die Zeitableitungen durch Raumableitungen ersetzen würden? Schauen wir mal, wohin uns das führt!

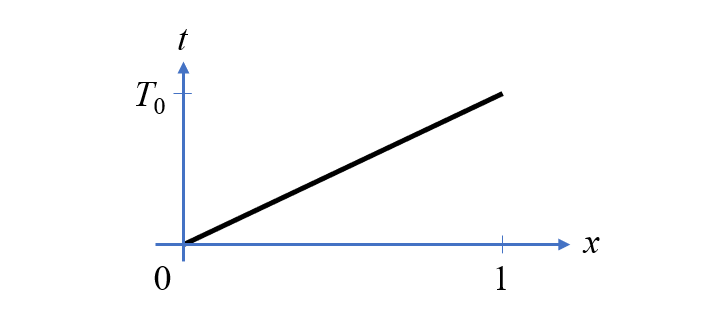
Zeit als Funktion der Position entlang eines 1D-Gebiets.

Wir betrachten ein 1D-Gebiet – eine gerade Linie mit Einheitslänge – in welchem wir zwei räumlich variierende Variablen entlang dieser Linie definieren, u_1 und u_2, und ein Netz entlang dieser Linie einführen, sodass COMSOL Multiphysics^® die Raumableitung, \partial u_1 / \partial x, über den Differentiationsoperator d(u1,x) bilden kann.

Da die räumliche Dimension für die zeitliche Dimension steht, handelt es sich hierbei eigentlich um die Zeitableitung. Mit diesem Gedanken im Hinterkopf können wir nun mit dem Interface Domain ODEs and DAEs eine algebraische Feldgleichung konstruieren, die über eine Strecke der Länge 1 definiert ist. Das Interface ist unten dargestellt, wo unsere beiden Unbekannten definiert sind. Wir werden für diese Felder Lagrange-Elemente verwenden, da dies automatisch ein kontinuierliches Feld gewährleistet und wir die Einheiten der Felder und der Quelle entsprechend einstellen können. Zur besseren Lesbarkeit können wir auch eine Reihe von Variablen definieren, die den Spannungsabfall aufgrund jeder Komponente des Schaltungsmodells beschreiben, wie in den folgenden Screenshots dargestellt.

Einrichten des Interfaces Domain ODEs and DAEs, Benennen der Feldvariablen, Auswählen der Formfunktion und Einstellen der Einheiten.

Die Variablen, die die angelegte Spannung im Zeit-Raum-Bereich definieren, die Ableitungen der Ströme und die Spannungsabfälle an den verschiedenen Komponenten des Schaltkreises.

Diese Variablen werden innerhalb des Features Algebraic Equation des Interfaces Domain ODEs and DAEs verwendet, das über zwei Felder für eine Gleichung verfügt, die immer gleich Null sein muss. Hier geben wir die Summe der potenziellen Abfälle sowie die Quelle für die beiden Stromschleifen ein. Dies sind die zuvor gezeigten Gleichungen. Schließlich werden zwei Pointwise Constraints zum Punkt an einem Ende des Gebiets hinzugefügt. Die Beschränkung basiert hier auf dem Feature Integration, das am anderen Punkt definiert ist. Die Beschränkung von u1-intop1(u1) und u2-intop1(u2) erzwingt die Periodizitätsbedingung.

Aufstellen der Gleichung, die überall in Zeit und Raum entlang des Einheitsgebiets erfüllt ist.

Definition des periodischen Zustands über Pointwise Constraint und das Feature Integration.

Die Lösung dieses stationären Problems erfordert ein relativ feines Netz entlang des Gebiets, wenn das Gerät in den nichtlinearen Bereich gebracht wird. Daher ist die Netzgröße entlang der Einheitslinie der eine Parameter, der bei der Lösung dieses nichtlinearen stationären Modells untersucht werden muss. Die Ergebnisse sind im folgenden Plot dargestellt und werden mit den transienten Ergebnissen verglichen, die eine hervorragende Übereinstimmung zeigen. Tatsächlich kann die geringe Abweichung reduziert werden, indem das transiente Modell mit noch engeren Toleranzen gelöst wird, wodurch die Rechenkosten selbst eines so kleinen Modells um etwa eine Minute steigen, während das stationäre Problem fast augenblicklich gelöst wird.

Vergleich der transienten Ergebnisse, die aus dem elektrischen Schaltungsmodell berechnet wurden, mit den stationären Ergebnissen des zeitperiodischen Ansatzes.

Die Lösung über eine Periode im Raum gibt uns auch die Möglichkeit, den Frequenzinhalt über den Datensatz Spatial FFT zu extrahieren. Die Einstellungen für dieses Feature sind in der folgenden Abbildung dargestellt, wobei ein Datensatz Array 1D hervorgehoben wird, der die Zeit-Raum-Lösung periodisch so strukturiert, dass die Ergebnisse glatter erscheinen. Durch den Plot einer entsprechend normalisierten Größe können wir sehen, wie der Frequenzinhalt mit zunehmender angelegter Spannung zunimmt.

Der Datensatz Spatial FFT verwendet als Eingabe den Array-1D-Datensatz, der die stationären Ergebnisse entlang der Zeitachse wiederholt.

Plot des Frequenzinhalts bei Erhöhung der Wechselspannung.

Abschließende Bemerkungen

In diesem Blog-Beitrag haben wir uns einen besonders attraktiven Ansatz angesehen, um den zeitperiodischen stationären Zustand eines Systems zu lösen, der durch eine Reihe algebraischer Gleichungen beschrieben werden kann. Beachten Sie, dass dieser Ansatz jede Art von Signal zulässt – nicht nur sinusförmige Anregungsfunktionen – solange es eine glatte und zeitperiodische Lösung gibt. Die Erstellung ist einfach und nutzt die Kernfunktionalität von COMSOL Multiphysics^®, wodurch dieser Ansatz für jede Art von Problem nützlich ist, nicht nur für elektrische Schaltungen. Er ist eine gute Technik, die COMSOL-Modellierer in ihrem Werkzeugkasten haben sollten.

Das dazugehörige Beispielmodell steht hier zum Download bereit: