Stufenförmige Drucklager (engl. step thrust bearings) nehmen Axialkräfte in rotierenden Maschinen auf. Da ihre Tragfähigkeit von der Geometrie abhängt, können Sie die Form- und Topologieoptimierung einsetzen, um die Tragfähigkeit eines Lagers zu maximieren. Bei der Formoptimierung wird die Form der Stufen des Lagers verändert, während bei der Topologieoptimierung eine implizite Geometriebeschreibung verwendet wird, sodass die Anzahl der Stufen variieren kann.
Einführung
Stufenförmige Drucklager können mit folgenden Annahmen modelliert werden:
- Die Dicke des Fluidfilms ist deutlich kleiner als die seitlichen Abmessungen des Lagers
- Trägheitseffekte können im Vergleich zu Schereffekten aufgrund des dünnen Schmiermittelfilms vernachlässigt werden
- Volumenkräfte sind vernachlässigbar
- Das Schmiermittel ist ein Newtonsches Fluid
- Geschwindigkeiten außerhalb der Ebene sind vernachlässigbar, weil das Seitenverhältnis des Ölfilms groß ist
- Die Geschwindigkeit hängt analytisch von den Koordinaten außerhalb der Ebene ab
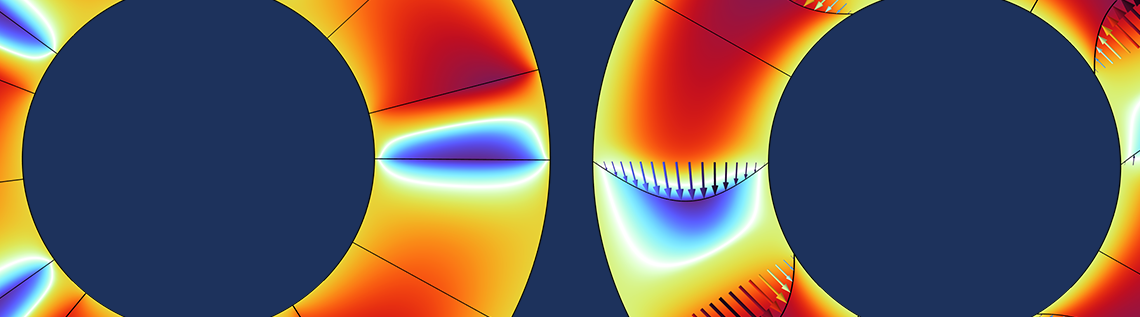
Die Annahmen 2-4 bedeuten, dass die Navier-Stokes-Gleichung zur Stokes-Gleichung vereinfacht werden kann, und die Annahmen 5-6 ermöglichen uns die Annahme, dass die Strömungsgeschwindigkeit proportional zum Druckgradienten ist. Mit diesen Punkten und den anderen Annahmen würde sich die maßgebliche Gleichung auf die Standard-Reynolds-Gleichung für den Druck reduzieren, aber hier wird stattdessen die Jakobsson-Floberg-Olsson-Theorie verwendet, damit die Kavitation berücksichtigt werden kann. Dies ist an der unten skizzierten Druckverteilung zu erkennen. Der Druck nimmt ab, wenn das Fluid die Engstelle durchläuft, und beginnt erst in der Nähe der nächsten Stufe in der nächsten Vertiefung zu steigen.
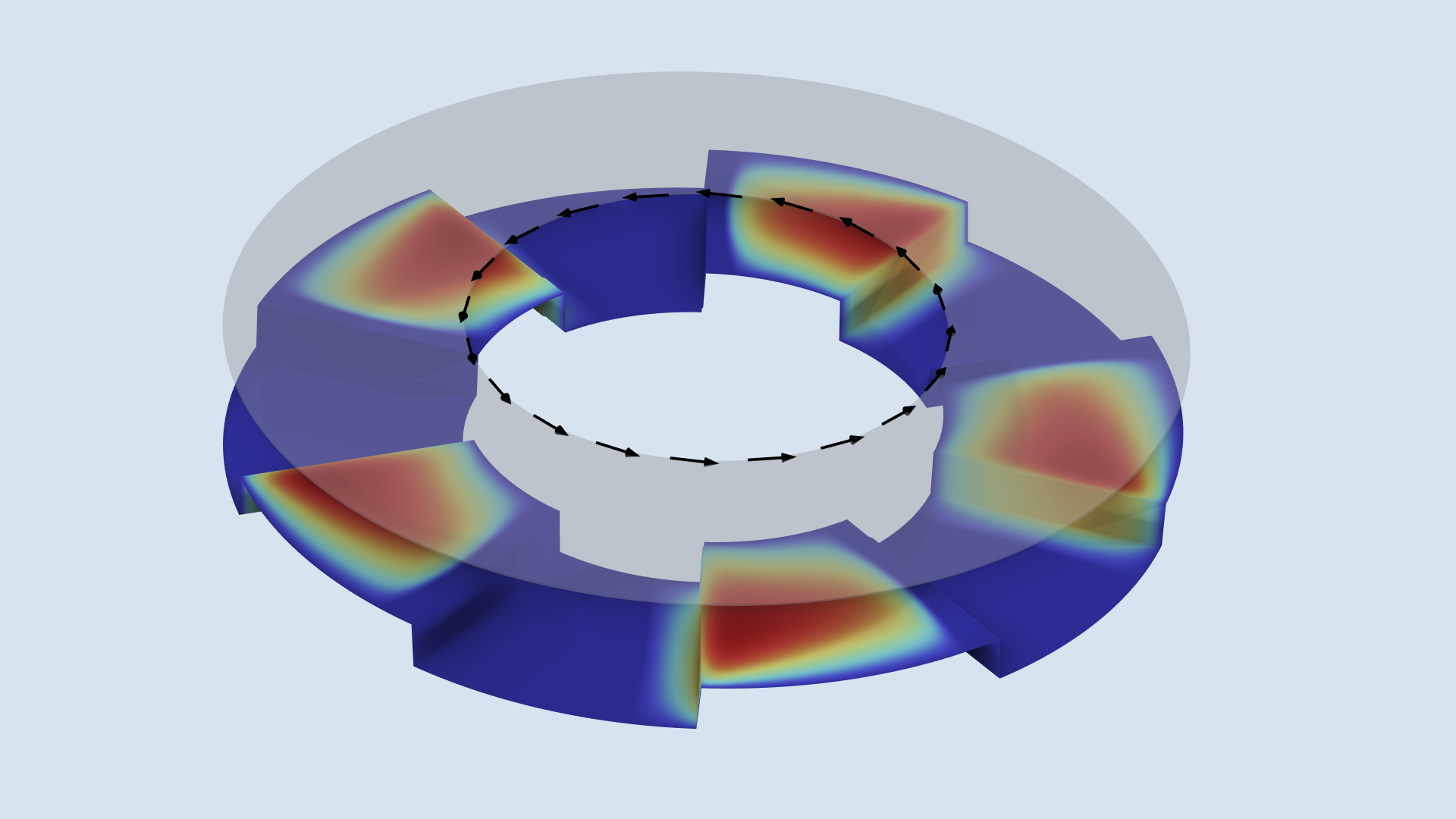
Eine Skizze eines stufenförmigen Drucklagers mit dem Druckring. Die Farben zeigen den Druck an. Die Stufen sind nicht explizit dreidimensional modelliert, so dass der Plot nicht das Berechnungsnetz darstellt.
Die Physik des Lagers wird mit dem Interface Hydrodynamic Bearing in der Software COMSOL Multiphysics® modelliert. Bei diesem Feature wird die Dimension außerhalb der Ebene nicht explizit berücksichtigt. Stattdessen wird eine planare Geometrie verwendet, und die Dickenänderung wird direkt in der Gleichung berücksichtigt, wie in der obigen Abbildung gezeigt.
Die Tragfähigkeit des Lagers hängt von der Druckverteilung ab, die ihrerseits von der Form der Stufen abhängt. Daher ist es sinnvoll, eine Formoptimierung durchzuführen, um die Tragfähigkeit zu maximieren:
wobei \boldmath{f}_\text{c} die auf den Druckring wirkende verteilte Kraft ist, die sich aus den Poiseuille-, Couette- und Normaldruckkomponenten zusammensetzt. Wie bereits erwähnt, berücksichtigt das Modell die Kavitation. Es wird jedoch nicht versucht, die Stärke der Kavitation zu begrenzen.
Formoptimierung
Bei der Formoptimierung wird eine bestehende Form mithilfe von Netzverformungen verändert. Das Interface Shape Optimization beinhaltet eine Reihe von Funktionen für diesen Zweck. In diesem speziellen Fall wird ein Feature der dritten Ordnung Polynomial Shell verwendet, bei dem die Verformung außerhalb der Ebene deaktiviert ist. Es wird für ein Set von Vorder- und Hinterkanten der Rastflächen angewandt und die Netzverformung wird dann mit der Funktion Sector Symmetry auf die anderen Rastflächen übertragen.
Der hier gezeigte Ansatz legt die Position der Punkte auf den kreisförmigen Rändern fest, aber es ist auch möglich, diese Punkte entlang der Ränder zu verschieben. Dies erfordert jedoch eine gleichungsbasierte Modellierung und separate Features Control Function für die hinteren und vorderen Kanten der Stufen, was die Einrichtung verkompliziert. Die größere Designfreiheit führt nur zu einer geringfügig besseren Leistung. Daher konzentriert sich dieser Blog-Beitrag auf den einfacheren Ansatz, aber die alternative Formulierung ist in der Application Library von COMSOL® Version 6.1 enthalten und kann weiterhin aus der Application Gallery heruntergeladen werden.
Das Ergebnis der Formoptimierung ist in der Abbildung unten dargestellt. Das Ergebnis hängt von der maximalen Verformung der Kanten sowie dem anfänglichen Winkel der Vertiefung ab. Die Optimierung führt zu einem Design, das das Öl in der Mitte zusammenpresst, bevor es über die Rastfläche gedrückt wird.
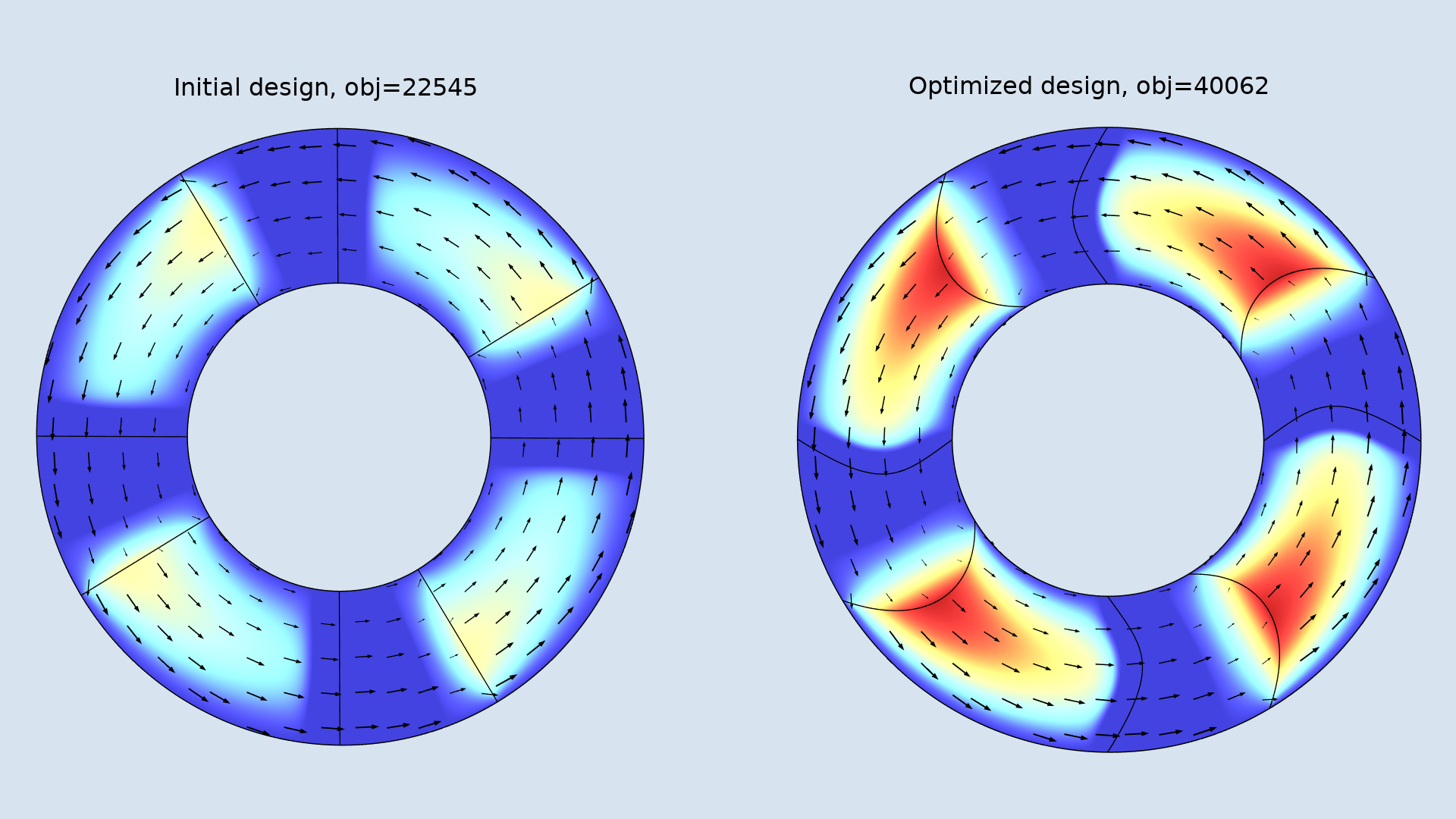
Das anfängliche Design (links) und das optimierte Design (rechts). Die durchschnittliche Fluidgeschwindigkeit ist mit Pfeilen dargestellt und die Farben zeigen die Druckverteilung.
Es ist empfehlenswert, die verformte Konfiguration durch eine erneute Vernetzung zu überprüfen. Die Überprüfung zeigt keine numerischen Probleme, wie Sie in der Version dieses Modells in der Application Library sehen können.
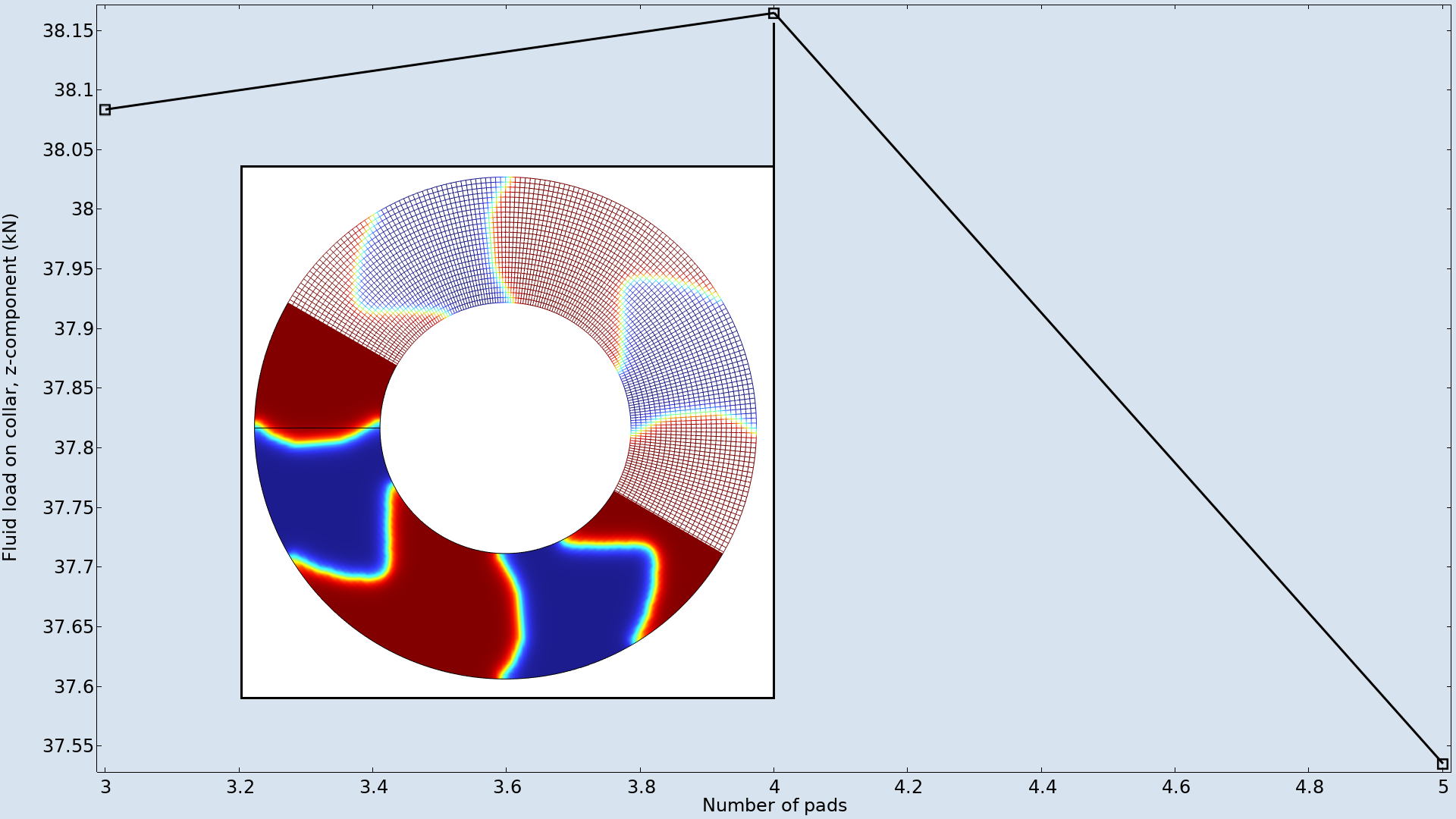
In diesem Beispiel werden die maximale Verformung und der Winkel der Vertiefung unabhängig von der Anzahl der Rastflächen festgelegt. Aus diesem Grund ist die optimale Rastflächenanzahl vier, wie unten dargestellt.
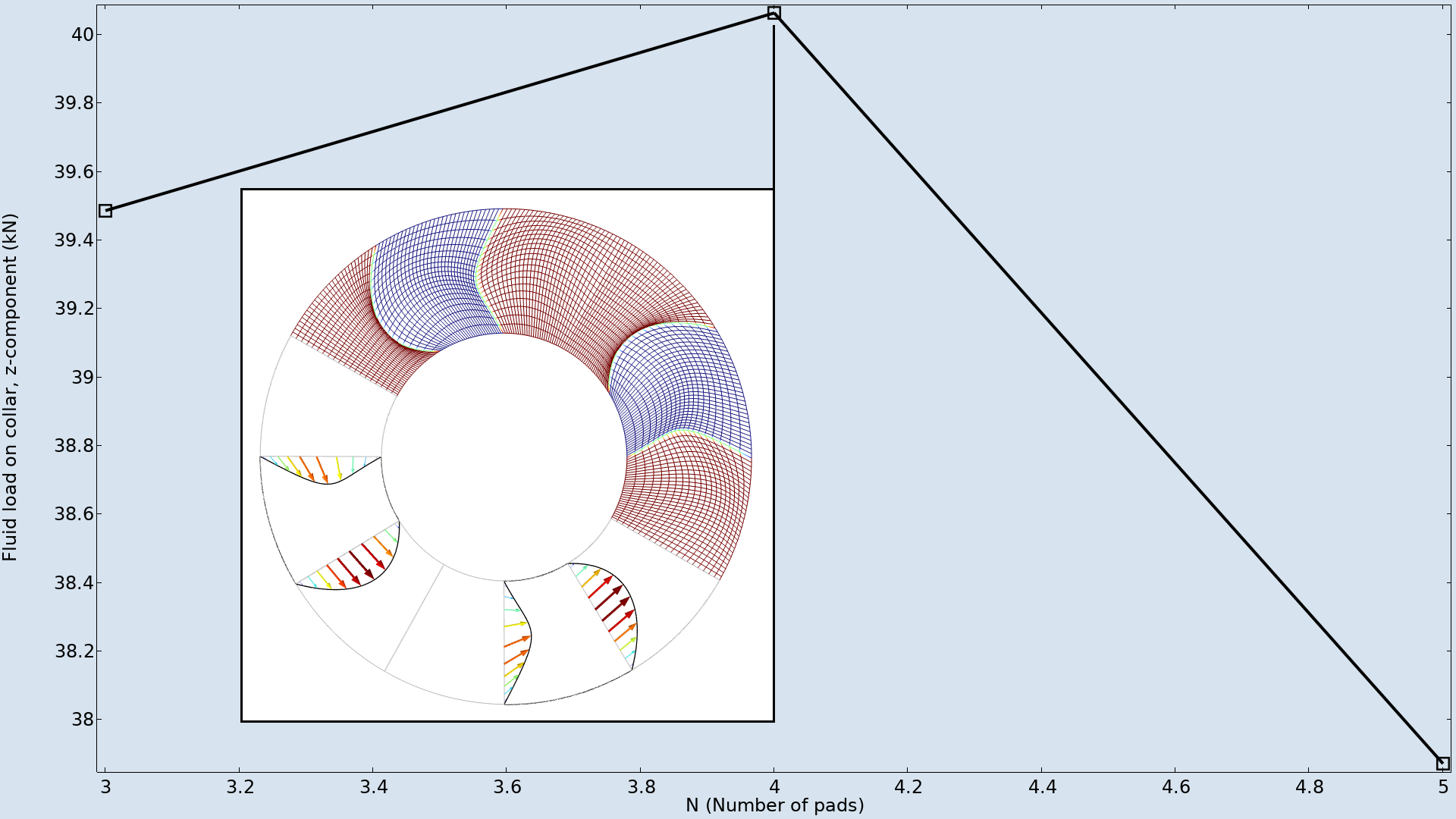
Die Formoptimierung wird für eine unterschiedliche Anzahl von Rastflächen durchgeführt und die resultierenden Ziele werden grafisch dargestellt. Das Maximum wird bei vier Rastflächen erreicht, und ein Einschub zeigt die Verformung des Netzes.
Die Formoptimierung funktioniert unabhängig von der Physik immer gleich und ist daher einfach einzurichten. Die Verzerrung des Netzes, die durch die Formoptimierung entsteht, ist begrenzt, um numerische Probleme zu vermeiden. Es steht dem Benutzer jedoch frei, mit der Balance zwischen großer Designfreiheit mit großer Leistungsverbesserung und kleiner Designfreiheit mit robuster Optimierung zu experimentieren. In jedem Fall ist das optimierte Design stark von der Ausgangsgeometrie abhängig, da die Topologie (und damit die Anzahl der Schritte) nur ein Input für die Optimierung sein kann, nicht aber ein Output. Die Topologieoptimierung kann dieses Problem behandeln, indem sie eine implizite Beschreibung der Geometrie einführt. Diese Methode kann ihre eigenen Nachteile haben, aber in diesem Fall kann sie ohne größere Schwierigkeiten angewandt werden.
Topologieoptimierung
Die Topologieoptimierung funktioniert durch die Einführung einer Designvariablen \theta_c für jedes Berechnungselement. Diese ist auf das geschlossene Intervall zwischen 0 und 1 beschränkt. Die Variable muss mit der Physik verbunden sein, so dass:
- Wo die Designvariable gleich 0 ist, werden die maßgeblichen Gleichungen für eine Vertiefung gelöst
- Wo die Designvariable gleich 1 ist, werden die maßgeblichen Gleichungen für ein Rastfläche gelöst
- Wenn die Designvariable zwischen 0 und 1 liegt, wird eine Gleichung gelöst, die die Gleichungen für eine Vertiefung und eine Rastfläche kombiniert
Der einzige Unterschied zwischen den Vertiefungen und den Rastflächen ist die Dicke des Ölfilms, h_f, so dass die oben genannten Anforderungen erfüllt sind, indem man diese Dicke von der Designvariablen abhängig macht. Bei anderen Topologieoptimierungsproblemen erfordern die Details des dritten Punktes besondere Aufmerksamkeit, aber in diesem Fall ist eine einfache lineare Interpolation ausreichend:
wobei \theta_f das in der Physik verwendete Feld und \theta_c das Steuervariablenfeld ist.
In diesem Fall kann \theta_c = \theta_f gesetzt werden. Die Konvergenz kann jedoch durch die Einführung eines Filters verbessert werden, der die kleine Längenskala im Steuervariablenfeld entfernt. Dies führt auch zu besseren Ergebnissen bei der Auswertung und Verifizierung der Ergebnisse. Der Filter kann als partielle Differentialgleichung (Helmholtz-Filter) ausgedrückt werden:
wobei R_\mathrm{min} die minimale Längenskala ist. (Nähere Einzelheiten über den Helmholtz-Filter und die Regularisierung in der Topologieoptimierung finden Sie in unserem Blog-Beitrag “Performing Topology Optimization with the Density Method”.)
Der Optimierung steht es frei, die Designvariable auf Zwischenwerte zu setzen. In diesem Fall könnte man dies als Zwischenwert für die Ölfilmdicke interpretieren, aber oft haben Zwischenwerte keine klare physikalische Darstellung – oder zumindest keine Darstellung, die von praktischer Relevanz ist. Dieses Problem scheint von Natur aus gut gestellt zu sein, da die Optimierung automatisch eine Lösung ohne Zwischenvariablen findet, d.h. es besteht eine klare Unterscheidung zwischen den Rastflächen und den Vertiefungen.
Es ist am besten, die Topologieoptimierung mit einem einheitlichen Wert der Designvariablen zu starten. Dies führt zu einem Design mit vier Rastflächen, aber man kann auch von einem uneinheitlichen Design ausgehen, um ein anderes lokales Optimum zu erreichen, wie in der Abbildung unten zu sehen.
Die Topologieoptimierung wird mit verschiedenen uneinheitlichen Ausgangsdesigns initialisiert, um bestimmte Topologien zu fördern. Der Plot zeigt, dass die optimale Rastflächenanzahl vier ist.
Bei diesen Einstellungen scheint es eine gute Übereinstimmung zwischen den Ergebnissen der Form- und der Topologieoptimierung zu geben.
Nach der Topologieoptimierung ist es ebenfalls sinnvoll, eine Verifizierungssimulation durchzuführen. Während die Verifizierung für die Formoptimierung jedoch dazu dient, numerische Probleme im Zusammenhang mit verformten Elementen zu überprüfen, dient die Verifizierung für die Topologieoptimierung dazu, Probleme im Zusammenhang mit der impliziten Geometriedarstellung zu überprüfen. Bei der Verifizierung für die Topologieoptimierung wird also eine explizite Geometriedarstellung verwendet, und dies führt zu einer deutlich besseren Zielfunktion, was darauf hindeutet, dass die implizite Geometriebeschreibung mit erheblichen Kosten verbunden ist. Eine weitere Untersuchung hat ergeben, dass es möglich ist, mit der Topologieoptimierung eine deutlich bessere Zielfunktion zu erhalten, wenn man ein feineres Netz verwendet, wie in der folgenden Animation zu sehen ist, in der das Design initialisiert wurde, um eine Topologie mit 16 Rastflächen zu erzeugen. Das resultierende Design ist qualitativ ähnlich wie die vorherigen Designs und ähnelt Drucklagern mit fischgrätenförmigen Vertiefungen (engl. herringbone-grooved thrust bearings).
Die Topologieoptimierung eines Lagers, das mit 16 Rastflächen initialisiert wurde.
Alle Optimierungen berücksichtigen eine feste Drehrichtung, und das ist in den optimierten Designs deutlich zu sehen. Das ursprüngliche Design ist symmetrisch in Bezug auf die Rotationsachse. Es ist also klar, dass die Leistung durch eine Lockerung dieser Einschränkung verbessert werden kann. Aus diesem Grund würde man auch kleinere Zielwerte erwarten, wenn beide Drehrichtungen bei der Optimierung berücksichtigt werden.
Fazit
Hier haben wir erörtert, wie die Form- und Topologieoptimierung für die Konstruktion von stufenförmigen Drucklagern verwendet werden kann. Der Aufbau der Physik und die hier besprochene Optimierung können in den folgenden Modellen und der dazugehörigen Dokumentation nachvollzogen werden:
- Formoptimierung eines stufenförmigen Drucklagers
- Topologieoptimierung eines stufenförmigen Drucklagers
Weitere Lernressourcen
Mehr über die Optimierung erfahren Sie In den folgenden Ressourcen:
- Informieren Sie sich über die Software-Erweiterungen, die die Optimierung von Drucklagern (und mehr!) ermöglichen:
- Sehen Sie sich diese Blog-Beiträge an, um mehr über die Topologieoptimierung in der Strukturmechanik zu lernen:



Kommentare (0)