
Die Modellierung von natürlicher und erzwungener Konvektion in COMSOL Multiphysics®
Immer wenn ein erwärmtes oder gekühltes Bauteil der Luft ausgesetzt ist, findet durch Konvektion eine Wärmeübertragung zwischen dem Bauteil und der Luft statt. Die Bewegung der Luft kann entweder durch einen Lüfter erzwungen werden oder frei sein, als Ergebnis der natürlichen Auftriebsschwankungen aufgrund von Änderungen der Lufttemperatur. Heute werden wir uns verschiedene Möglichkeiten zur Modellierung dieser Arten von Konvektion in der COMSOL Multiphysics®-Software ansehen.
Ein einfaches Beispiel zum Anfang: Der Wärmeübergangskoeffizient
Betrachten wir zunächst ein Modell der elektrischen Erwärmung einer Stromschiene, das unten abgebildet ist. Vielleicht kennen Sie dieses Beispiel aus der Einführung in COMSOL Multiphysics®, aber wenn Sie es noch nicht modelliert haben, empfehlen wir Ihnen, sich dieses Modell vorab anhand der PDF-Broschüre Introduction to COMSOL Multiphysics® anzusehen.
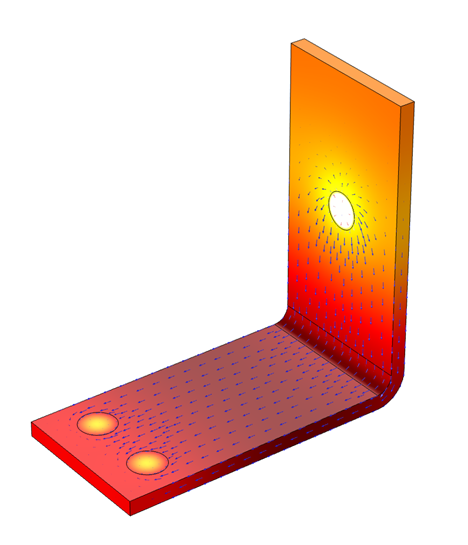
Elektrische Ströme (Pfeildiagramm), die durch eine Stromschiene aus Metall fließen, führen zu einer Widerstandserwärmung, die die Temperatur erhöht (Farbflächendiagramm).
In diesem Beispiel modellieren wir einen elektrischen Strom, der durch eine Stromschiene fließt. Dies führt zu einer Widerstandserwärmung, die wiederum die Temperatur der Stromschiene ansteigen lässt. Wir gehen davon aus, dass nur Wärme an die Umgebungsluft übertragen wird und vernachlässigen die Wärmeübertragung durch die Schrauben und die Strahlungswärme. Das Beispiel geht zunächst auch davon aus, dass es keinen Lüfter gibt, der Luft über die Stromschiene bläst. Die Wärmeübertragung an die Luft erfolgt also durch natürliche, d. h. freie, Konvektion.
Wenn das Element die Umgebungsluft erwärmt, wird die Luft heißer. Mit zunehmender Erwärmung nimmt die Dichte der Luft ab, wodurch die heiße Luft gegenüber der kühleren Umgebungsluft aufsteigt. Diese freien konvektiven Luftströme erhöhen die Wärmetransportrate von dem Element an die Umgebungsluft. Die Luftströme hängen von den Temperaturschwankungen sowie von der Geometrie des Elements und seiner Umgebung ab. Konvektion kann natürlich auch in anderen Gasen oder Fluidkeiten wie Wasser oder Transformatorenöl auftreten, aber wir werden uns in dieser Diskussion hauptsächlich auf die Konvektion in Luft konzentrieren.
Wir können den umgebenden Luftraum in eine von zwei Kategorien einteilen: Intern oderr Extern. Intern bedeutet, dass es einen begrenzten Hohlraum (z. B. eine elektrische Anschlussdose) um das Element herum gibt, in dem die Luft einigermaßen gut eingeschlossen ist, obwohl es bekannte Luftein- und -auslässe zu einem externen Raum geben könnte. Wir gehen dann davon aus, dass die thermischen Randbedingungen an der Außenseite des Hohlraums und an den Ein- und Auslässen bekannt sind. Andererseits impliziert Extern, dass das Objekt von einem im Grunde unendlich großen Luftvolumen umgeben ist. Wir gehen dann davon aus, dass die Lufttemperatur weit weg vom Objekt ein konstanter, bekannter Wert ist.
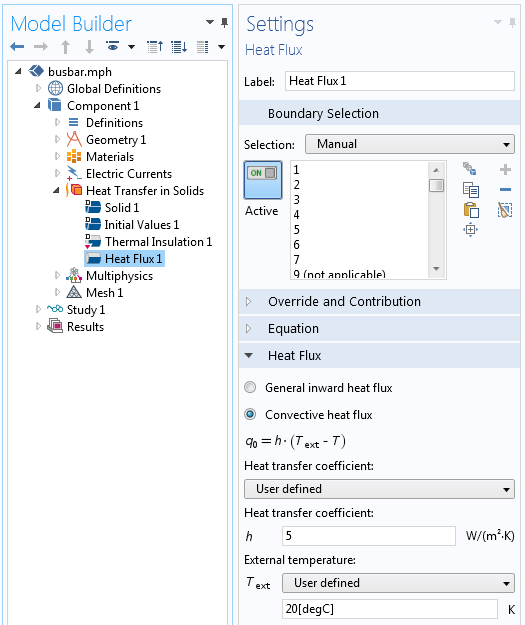
Die Einstellungen für einen konstanten Wärmeübergangskoeffizienten.
Das einleitende Stromschienen-Beispiel geht von einem freien konvektiven Wärmetransport an einen externen Luftraum aus. Dies wird mit der folgenden Randbedingung für den Wärmestrom modelliert:
wobei die externe Lufttemperatur Text = 25°C ist und h=5 W/m^2K der Wärmeübergangskoeffizient.
Dieser aus einem Wert bestehende Wärmeübergangskoeffizient stellt einen Näherungs- und Durchschnittswert für alle lokalen Schwankungen der Luftströmungen dar. Selbst für dieses einfache System könnte jeder Wert zwischen h\approx 2-25 W/m^2K ein angemessener Wärmeübergangskoeffizient sein, und es lohnt sich, verschiedene Fälle auszuprobieren und die Ergebnisse zu vergleichen.
Wenn wir stattdessen wissen, dass ein Ventilator Luft über diese Struktur bläst, dann verwenden wir aufgrund der schnelleren Luftströmungen einen Wärmeübergangskoeffizienten von ca. 10-250 W/m^2K, um den verstärkten Wärmetransport darzustellen.
Handelt es sich bei dem umgebenden Fluid um eine Flüssigkeit wie z. B. Wasser, so ist der Wertebereich der freien und erzwungenen Wärmeübergangskoeffizienten viel breiter. Für die freie Konvektion in einer Flüssigkeit liegt die typische Spanne bei ca. 50-1.000 W/m^2K. Für die erzwungene Konvektion ist die Spanne sogar noch breiter: h\approx 50-20,000 W/m^2K.
Mit der Eingabe eines einzigen Wertes für den Wärmeübergangskoeffizienten für die freie oder erzwungene Konvektion vereinfachen wir das Problem eindeutig zu stark, warum also machen wir das? Zunächst weil es einfach zu implementieren ist und wir den besten und schlechtesten Fall leicht vergleichen können. Außerdem kann diese Randbedingung mit dem Grundmodul von COMSOL Multiphysics® angewandt werden. Es gibt jedoch auch anspruchsvollere Ansätze innerhalb des Heat Transfer Module und des CFD Module, die wir uns als Nächstes ansehen wollen.
Konvektive Korrelationen verwenden
Eine konvektive Korrelation ist eine empirische Beziehung, die für gängige Geometrien entwickelt wurde. Bei Verwendung des Heat Transfer Module oder des CFD Module sind diese Korrelationen in der Randbedingung Heat Flux verfügbar, wie im folgenden Screenshot dargestellt.
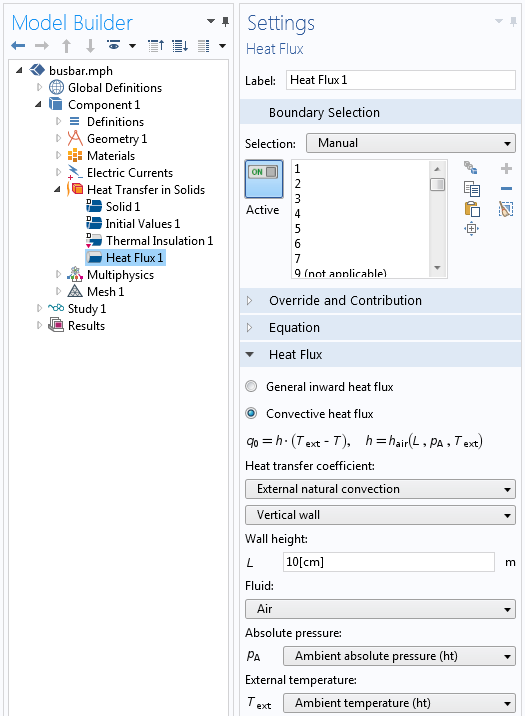
Die Randbedingung Heat Flux mit externer natürlicher konvektiver Korrelation für eine senkrechte Wand.
Die Verwendung dieser Korrelationen erfordert die Eingabe der charakteristischen Abmessungen des Elements. Für unser Stromschienenmodell verwenden wir beispielsweise die Korrelation External natural convection, Vertical wall und wählen eine Wandhöhe von 10 cm, um den freien konvektiven Wärmestrom an den vertikalen Flächen der Stromschiene zu modellieren. Wir müssen auch die externe Lufttemperatur und den Luftdruck angeben. Diese Werte können wir aus der ASHRAE-Datenbank laden, ein Prozess, den wir in einem vorhergehenden Blog-Beitrag beschrieben haben.
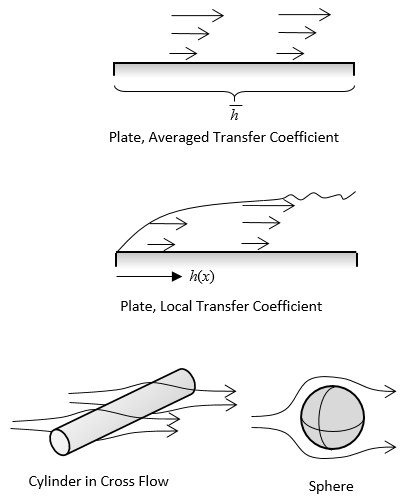
Die nachstehende Tabelle enthält Schemata für alle verfügbaren Korrelationen. Diese nehmen die Informationen über die Oberflächengeometrie und verwenden eine Nusselt-Zahl-Korrelation um den Wärmeübergangskoeffizienten zu berechnen.
Wenn Sie die Korrelationen für erzwungene Konvektion verwenden, müssen Sie auch die Luftgeschwindigkeit angeben. Diese konvektiven Korrelationen haben den Vorteil, dass sie die Realität genauer abbilden, da sie auf etablierten experimentellen Daten basieren. Diese Korrelationen führen zu einer nichtlinearen Randbedingung, was jedoch in der Regel nur geringfügig längere Berechnungszeiten zur Folge hat als bei Verwendung eines konstanten Wärmeübergangskoeffizienten. Der Nachteil ist, dass sie nur dann verwendet werden können, wenn es eine empirische Beziehung gibt, die für die Elementgeometrie angemessen ist.
| Freie Konvektion | Erzwungene Konvektion | |
|---|---|---|
| Extern | 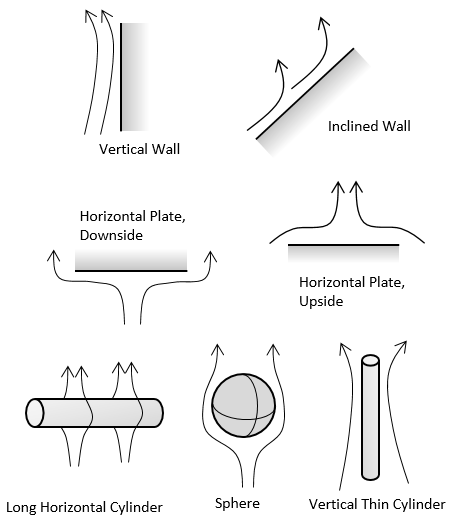 |
 |
| Intern | 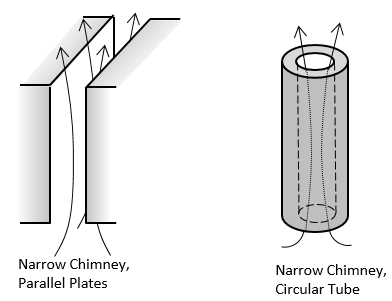 |
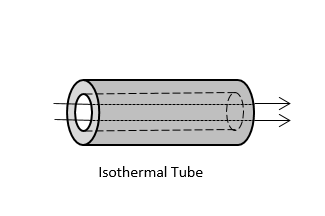 |
Die verfügbaren Randbedingungen für konvektive Korrelationen.
Beachtenswert ist, dass alle oben genannten konvektiven Korrelationen, auch die, die als intern eingestuft sind, das Vorhandensein eines unendlichen externen Fluidreservoirs voraussetzen, z. B. den umgebenden Luftraum. Die von den Oberflächen abgeführte Wärme geht in diesen Luftraum über, ohne dessen Temperatur zu verändern, und die einströmende Umgebungsluft hat eine bekannte Temperatur. Handelt es sich jedoch um Konvektion in einem vollständig umschlossenen Behälter, dann ist keine dieser Korrelationen angemessen und wir müssen zu einem anderen Modellierungsansatz übergehen.
Annäherung an die freie Konvektion in einem Gehäuse mithilfe einer verbesserten Wärmeleitfähigkeit
Betrachten wir einen rechteckigen luftgefüllten Hohlraum. Wenn dieser Hohlraum an einer der vertikalen Seiten beheizt und an der anderen Seite gekühlt wird, kommt es zu einer regelmäßigen Luftzirkulation. Ebenso findet eine Luftzirkulation statt, wenn der Hohlraum von unten beheizt und von oben gekühlt wird. Diese Fälle sind in den folgenden Bildern dargestellt, die durch Auflösen nach der Temperaturverteilung und dem Luftstrom erzeugt wurden.
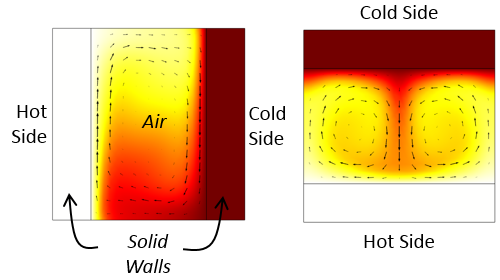
Freie konvektive Ströme in vertikal und horizontal ausgerichteten rechteckigen Hohlräumen.
Das Auflösen nach den freien konvektiven Strömen ist ziemlich kompliziert. Ein Beispiel finden Sie in diesen Blog-Beitrag über die Modellierung natürlicher Konvektion. Daher suchen wir eine einfachere Alternative. Innerhalb des Heat Transfer Module gibt es die Möglichkeit, die Funktion Equivalent conductivity for convection zu verwenden. Bei Verwendung dieser Funktion ist die effektive Wärmeleitfähigkeit der Luft auf der Grundlage von Korrelationen für horizontale und vertikale rechteckige Hohlräume erhöht, wie in der folgende Screenshot zeigt.
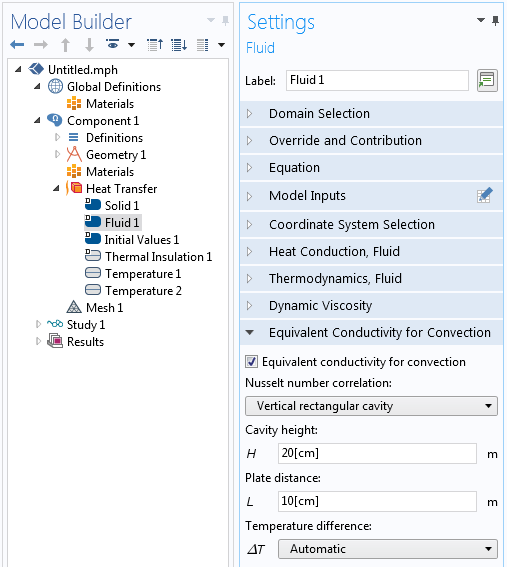
Die Equivalent conductivity for convection Funktion und Einstellungen.
Das luftgefüllte Gebiet wird noch immer expliziert modelliert (mithilfe des Fluid Feature innerhalb des Heat Transfer Interface), aber die Strömungsfelder der Luft werden nicht berechnet und die Geschwindigkeit wird schlicht vernachlässigt. Die Wärmeleitfähigkeit wird durch einen empirischen Korrelationsfaktor erhöht, der von den Dimensionen des Hohlraums und den Temperaturschwankungen im Hohlraum abhängt. Die Dimensionen des Hohlraums müssen angegeben werden, aber die Software kann die Temperaturunterschiede im Hohlraum automatisch berechnen und aktualisieren.
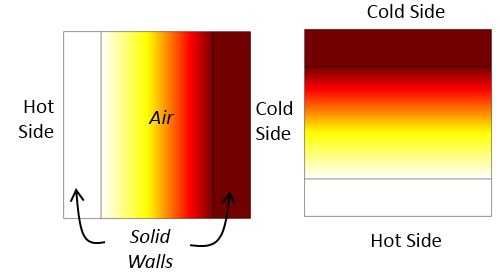
Temperaturverteilung in vertikal und horizontal ausgerichteten Hohlräumen, berechnet mit dem Feature Equivalent conductivity for convection. Die freien konvektiven Luftströme werden nicht berechnet. Stattdessen ist die Wärmeleitfähigkeit der Luft erhöht.
Dieser Ansatz zur Annäherung an die freie Konvektion in einem vollständig geschlossenen Hohlraum erfordert, dass wir den Luftgebiet vernetzen und das Temperaturfeld in der Luft lösen, was jedoch in der Regel nur einen geringen Rechenaufwand bedeutet. Der Nachteil dieses Ansatzes besteht darin, dass er für nicht rechteckige Geometrien nicht sehr gut geeignet ist.
Schätzung der erzwungenen Konvektion in einem Gehäuse mithilfe isothermischer Gebiete
Betrachten wir als Nächstes ein vollständig abgedichtetes Gehäuse mit einem Ventilator oder Gebläse, das die Luft aktiv durchmischt. Wir können davon ausgehen, dass sich im gesamten Hohlraum gut gemischte Luft mit einer konstanten Temperatur befindet. In diesem Fall kann das Isothermal Domain Feature genutzt werden, das über das Heat Transfer Module verfügbar ist, wenn in den Einstellungen die Isothermal domain Option ausgewählt wurde.
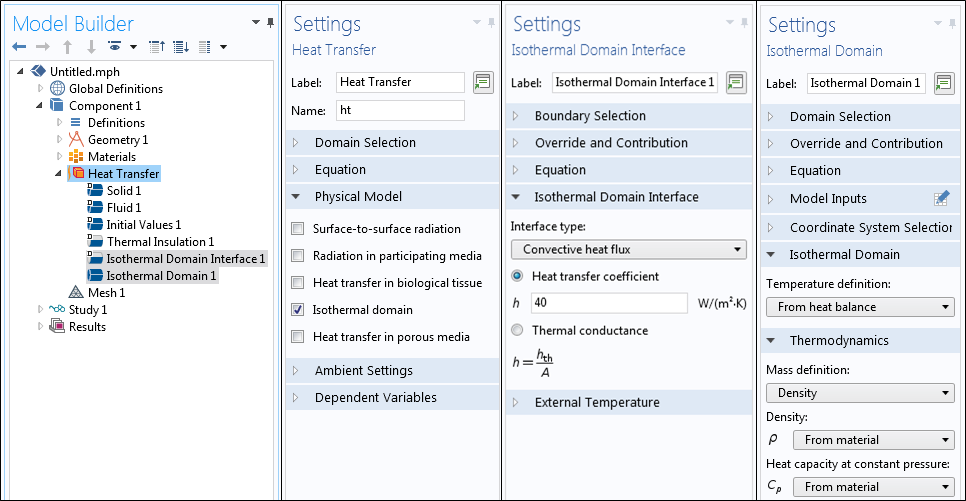
Die Einstellungen für das Interface Isothermal Domain.
Eine gut durchmischtes Luftgebiet kann mit dem Feature Isothermal Domain explizit modelliert werden. In dem Modell ist die Temperatur des gesamten Bereichs ein konstanter Wert. Die Temperatur der Luft wird auf der Grundlage der Wärmebilanz berechnet, die über die Ränder in den Bereich eintritt und ihn verlässt. Die Ränder des Isothermalbereichs können mit einer der folgenden Optionen festgelegt werden:
- Thermally Insulated: Kein Wärmetransport über den Rand
- Continuity: Kontinuität der Temperatur über den Rand
- Ventilation: Ein bekannter Fluidkeitsstrom bekannter Temperatur in den oder aus dem Isothermalbereich
- Convective Heat Flux: Ein von dem Anwender spezifizierter Koeffizient für den Wärmetransport, wie zuvor beschrieben
- Thermal Contact: Ein spezifischer thermischer Widerstand
Von diesen Optionen für mögliche Randbedingungen ist Convective Heat Flux die Angemessenste für gut durchmischte Luft in einem geschlossenen Hohlraum.
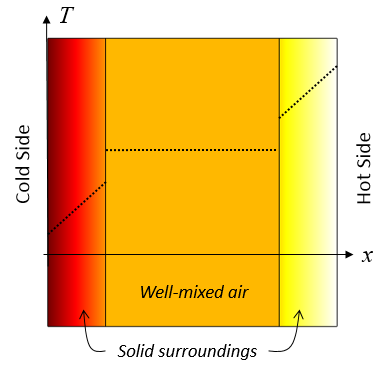
Representative Ergebnisse des Isothermal Domain Features. Der gutdurchmischte Luftbereich hat eine konstante Temperatur und es findet Wärmetransport zu den umgebenden festen Bereichen statt, der über einen spezifizierten Koeffizienten für den Wärmetransport definiert wird.
Explizierte Modellierung der Luftströmung
Der rechenintensivste , aber auch der allgemeinste Ansatz ist die explizite Modellierung der Luftströmung. Wir können sowohl erzwungene als auch freie Konvektion modellieren sowie eine interne oder externe Strömung simulieren. Diese Art der Modellierung kann entweder mit dem Heat Transfer Module oder mit dem CFD Module durchgeführt werden.
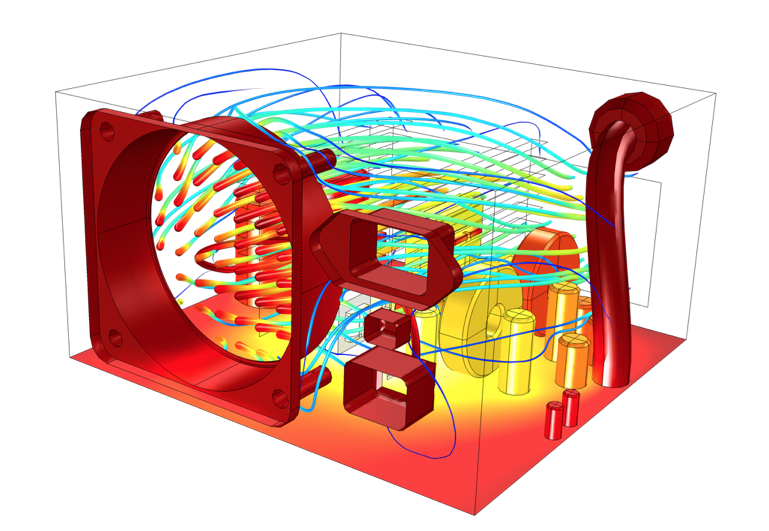
Ein Beispiel der Berechnung der Luftströmung und der Temperatur in einem Gehäuse.
Wenn Sie die Broschüre Introduction to COMSOL Multiphysics® gelesen haben, haben Sie bereits ein Beispiel für ein Modell der internen erzwungenen Konvektion gelöst. Sie können mehr über die explizite Modellierung von Luftströmungen in den am Ende dieses Beitrags erwähnten Ressourcen erfahren.
Wann können wir die freie Konvektion ganz ignorieren?
Zum Abschluss dieses Themas werden wir uns mit folgender Frage beschäftigen: Wann kann die freie Konvektion in Luft vernachlässigt werden und wie können wir diese Fälle modellieren? Wenn die Abmessungen eines Hohlraums sehr klein sind, z. B. bei einem dünnen Spalt zwischen Komponenten oder einem sehr dünnen Rohr, besteht die Möglichkeit, dass die viskose Dämpfung größer ist als alle Auftriebskräfte. Dieses Gleichgewicht zwischen viskosen und Auftriebskräften wird durch die nichtdimensionale Rayleigh-Zahl charakterisiert. Das Einsetzen der freien Konvektion kann je nach Randbedingungen und Geometrie sehr unterschiedlich sein. Eine gute Faustregel besagt, dass bei Abmessungen von weniger als 1 mm wahrscheinlich keine freie Konvektion auftritt, aber sobald die Abmessungen des Hohlraums größer als 1 cm sind, wird es wahrscheinlich freie Konvektionsströme geben.
Wie können wir also den Wärmetransport durch diese kleinen Lücken modellieren? Wenn kein Luftstrom vorhanden ist, können diese luftgefüllten Bereiche einfach als Festkörper oder als Fluid ohne Konvektionsterm modelliert werden. Dies wird in der Anleitung Window and Glazing Thermal Performances gezeigt. Die Luft kann auch als Festkörper innerhalb einer mikroskaligen geschlossenen Struktur modelliert werden.
Wenn diese dünnen Lücken im Vergleich zu den anderen Dimensionen des zu analysierenden Systems sehr klein sind, können Sie die Lücken weiter vereinfachen, indem Sie sie über die Randbedingung Thin Layer mit dem Schichttyp Thermal Thick Approximation modellieren. Diese Randbedingung führt einen Temperatursprung über die innere Ränder ein, der auf der angegebenen Dicke und Wärmeleitfähigkeit basiert.
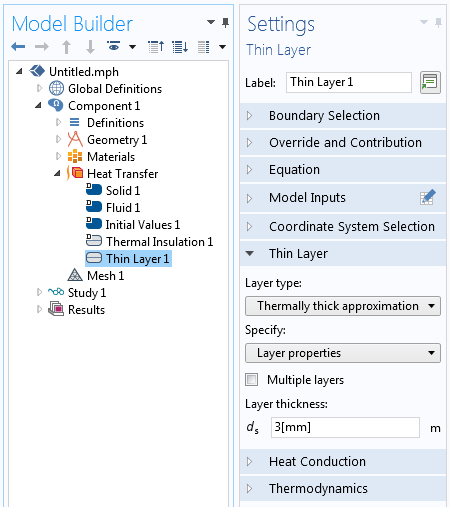
Die Thin Layer Randbedingung kann schmale Luftlücken zwischen den Elementen modellieren.
Die beiden vorgenannten Ansätze können wir innerhalb des COMSOL Multiphysics® Grundmoduls anwenden. Im Heat Transfer Module gibt es zusätzliche Optionen für die Thin Layer Bedingung, um allgemeinere und mehrschichtige Ränder zu berücksichtigen, die aus mehreren Materialschichten bestehen können.
Abschließende Bemerkungen zur Modellierung von natürlicher und erzwungener Konvektion in COMSOL Multiphysics®
Bevor wir diese Diskussion abschließen, sollten wir noch kurz auf die Frage des Wärmetransports über Strahlung eingehen. Obwohl wir hier nicht über Strahlung gesprochen haben, muss ein Ingenieur sie immer in Betracht ziehen. Oberflächen, die den Umgebungsbedingungen ausgesetzt sind, strahlen Wärme an die Umgebung ab und werden von der Sonne aufgeheizt. Das Ausmaß der Strahlungswärme der Sonne ist beträchtlich – etwa 1000 Watt pro Quadratmeter – und sollte nicht vernachlässigt werden. Einzelheiten zur Modellierung des Wärmetransports über Strahlung an die Umgebung finden Sie in diesem vorherigen Blog-Beitrag.
Außerdem findet zwischen den inneren Oberflächen Wärmetransport durch Strahlung statt. Der Wärmestrom zwischen den Oberflächen ist eine Funktion der Temperaturdifferenz in vierter Potenz. Bedenken Sie, dass der Wärmetransport durch Strahlung zwischen zwei Oberflächen bei 20°C und 50°C höchstens 200 Watt pro Quadratmeter beträgt, bei Oberflächen von 20°C und 125°C jedoch auf 1000 Watt pro Quadratmeter ansteigt. Um den Wärmetransport durch Strahlung zwischen Oberflächen korrekt zu berechnen, ist es auch wichtig, die Ansichtsfaktoren mit dem Heat Transfer Module zu berechnen.
Heute haben wir uns verschiedene Ansätze zur Modellierung der Konvektion angesehen, beginnend mit dem einfachsten Ansatz der Verwendung eines konstanten konvektiven Wärmeübergangskoeffizienten. Anschließend haben wir die Verwendung einer empirischen konvektiven Korrelations-Randbedingung erörtert, bevor wir uns mit der Verwendung einer effektiven Wärmeleitfähigkeit innerhalb eines Bereichs und einer Funktion für den isothermen Bereich befasst haben – Ansätze mit höherer Genauigkeit und nur geringfügig höheren Rechenkosten. Der rechenintensivste Ansatz – die explizite Berechnung des Strömungsfeldes – ist natürlich auch der allgemeinste. Wir sind auch darauf eingegangen, wann es angebracht ist, die freie Konvektion vollständig zu vernachlässigen und wie man solche Situationen modelliert. Sie sollten nun ein besseres Verständnis für die verfügbaren Optionen und Kompromisse bei der Modellierung von freier und erzwungener Konvektion haben. Viel Spaß beim Modellieren!
Zusätzliche Ressourcen
- Erfahren Sie mehr über die explizierte Modellierung von Luftströmungen und Wärmetransport, im COMSOL Blog:
- Erhalten Sie eine Einführung in die Modellierung von Wärmetransport in einem archivierten Webinar




Kommentare (0)