
Mit dem Release von Version 6.2 der Software COMSOL Multiphysics® wurden die Funktionen zur Modellierung der elektrischen Dispersion auf das Interface Electric Currents erweitert, das sowohl die Modellierung im Zeit- als auch im Frequenzbereich unterstützt. Diese Funktionalität ist besonders wichtig für die genaue Modellierung eines breiten Spektrums von Materialien, einschließlich Isolatoren und lebendem Gewebe. Besprechen wir kurz, was Dispersion ist, und dann zeigen wir Ihnen, wie Sie sie in Ihre COMSOL-Modelle einbeziehen können und warum sie so wichtig ist.
Hintergrund
Bei der Modellierung schneller Strompulse, die auf lebendes Gewebe einwirken, wie zum Beispiel bei der Herzablation, der Elektroporation oder der Nervenstimulation, müssen die dispersiven Eigenschaften des Gewebes und der elektrischen Isolatoren berücksichtigt werden.
Alle Materialien sind elektrisch dispersiv, d.h. die relative Dielektrizitätskonstante variiert mit der Anregungsfrequenz. Die Dielektrizitätskonstante ist ein Maß dafür, wie ein Material in Gegenwart eines elektrischen Feldes reagiert bzw. sich polarisiert. Das Ausmaß dieser Reaktion variiert mit der Frequenz aufgrund der verschiedenen Atome und Moleküle im Material und deren Struktur. Sie ist auch ein Maß dafür, wie viel elektrische Energie in Wärme umgewandelt wird oder verloren geht, wenn das Material einem zeitlich veränderlichen Signal ausgesetzt ist. Diese Verluste entstehen durch die relative Bewegung der Atome und Moleküle, die in den zeitlich veränderlichen Feldern schwingen. Bei der Arbeit im Frequenzbereich wird die relative Permittivität als komplexe Zahl ausgedrückt: \epsilon_r =\epsilon_r^{‘}- i \epsilon_r^{”}, wobei der Real- und der Imaginärteil durch die Kramers-Kronig-Beziehungen in Beziehung gesetzt werden. In der folgenden Abbildung sind zwei solcher Dispersionskurven dargestellt, die ein isolierendes Material bzw. lebendes Gewebe repräsentieren. Ersteres hat eine relativ einfache Kurve mit fast gleichmäßigen Eigenschaften über ein breites Frequenzband. Daran können wir sehen, dass es nicht immer nötig ist, die Dispersion zu einzubeziehen. Andererseits wird es immer ein Frequenzband geben, in dem die Eigenschaften erheblich variieren, so dass eine Berücksichtigung der Dispersion notwendig ist.
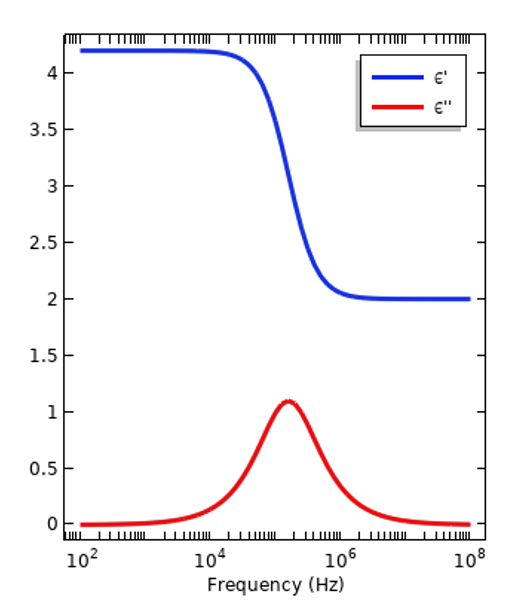
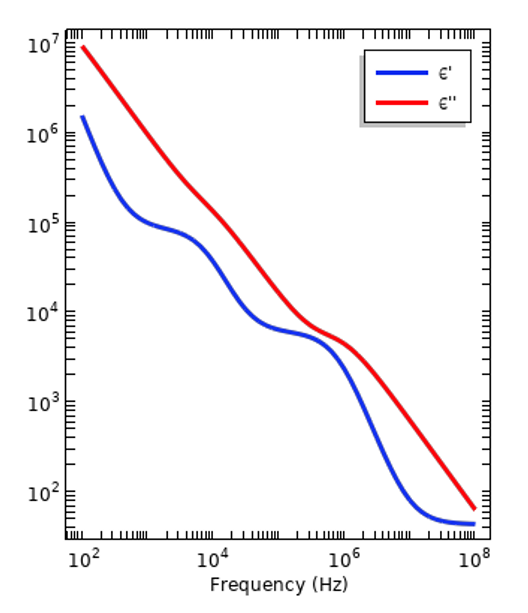
Repräsentative Dispersionskurven eines Isolators (links) und von menschlichem Gewebe (rechts). Dargestellt sind der Real- und Imaginärteil der relativen Permittivität.
Zusätzlich zu diesen frequenzabhängigen Verlusten gibt es auch elektrische Verluste in einem statischen elektrischen Feld. Diese werden durch die elektrische Gleichstromleitfähigkeit \sigma_{DC} quantifiziert. Alle Materialien haben eine gewisse Gleichstromleitfähigkeit, die jedoch sehr, sehr gering sein kann. Dies ist ein anderer Verlustmechanismus als der Dispersionsverlust. Es kann sinnvoll sein, alle Materialverluste, unabhängig vom Mechanismus, durch die Gesamtleitfähigkeit auszudrücken: \sigma_{tot} =\sigma_{DC} + 2\pi f \epsilon_0\epsilon_r^{”}. Dies ist unten für dieselben beiden Materialien aufgetragen. Es ist jedoch wichtig zu beachten, dass die frequenzabhängige Leitfähigkeit auch ohne die Gleichstromkomponente dargestellt werden kann: \sigma(f) = 2\pi f \epsilon_0\epsilon_r^{”} wobei \sigma_{DC} separat angegeben wird.
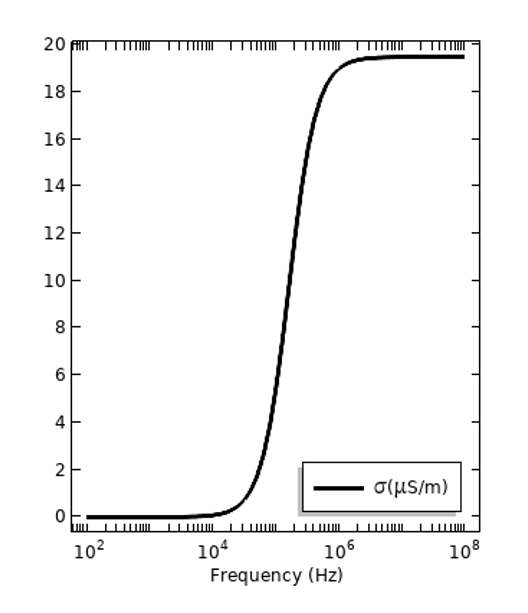
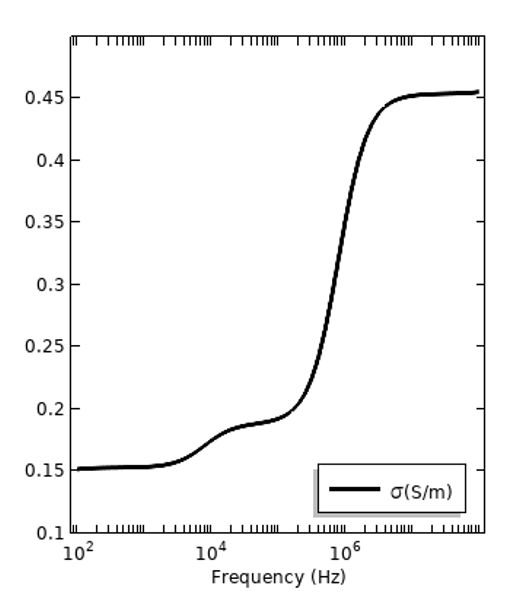
Die Verluste der selben beiden Materialien in Bezug auf die elektrische Gesamtleitfähigkeit, wobei die Gleichstromleitfähigkeit als Beitrag zum Dispersionsverlust dargestellt wird.
Obwohl die Materialeigenschaften experimentell bestimmt werden, wollen wir die experimentellen Daten nicht direkt verwenden, da sie mit einer gewissen Unsicherheit behaftet sind und die Kramers-Kronig-Beziehungen nicht erfüllen, was zu einem nicht-kausalen Modell führten würde. Stattdessen passen wir an die Daten eine Funktion an, die bereits die Kramers-Kronig-Beziehungen erfüllt, und verwenden die Koeffizienten dieser angepassten Funktion, um unser Materialverhalten zu beschreiben. Derzeit unterstützt die Software das Modell Multipole Debye, das als Eingabe eine beliebige Anzahl von Polen, N, akzeptiert, wobei jeder Pol, m, eine Relaxationszeit, \tau_m, und Beiträge zur relativen Dielektrizitätskonstante, \Delta \epsilon_r_m, besitzt und aus diesen die komplexwertige Dielektrizitätskonstante wie folgt definiert:
wobei \epsilon_\infty entweder auf der Niederfrequenzgrenze, \epsilon_\infty \rightarrow \epsilon_{rS}-\Sigma \Delta \epsilon_r_m, oder auf der Hochfrequenzgrenze, \epsilon_\infty \rightarrow \epsilon_{rS}, basiert. Darüber hinaus können die Relaxationszeiten optional aufgrund einer Temperaturänderung verschoben werden, indem eine der Verschiebungsfunktionen Vogel-Fulcher, Arrhenius, Williams-Landel-Ferry oder Tool-Narayanaswamy-Moyniha oder sogar eine benutzerdefinierte Verschiebungsfunktion verwendet wird.
Wenn Sie experimentelle Daten für den Real- und Imaginärteil der Dielektrizitätskonstante haben und ein Debye-Modell an diese Daten anpassen möchten, können Sie dies mit der Funktion Partial Fraction Fit in COMSOL® Version 6.2 tun. Eine Anleitung zur Verwendung dieser Funktionalität finden Sie in dem Artikel “Fitting the Debye Dispersion Model to Experimental Data” in unserem Learning Center.
Verwendung von Electric Currents
Die Einbeziehung der Dispersion in ein Modell mit dem Interface Electric Currents erfordert nur ein paar Schritte. Zunächst muss das Feature Current Conservation hinzugefügt und auf die relevanten Gebiete angewendet werden. Innerhalb dieses Features muss der Material Type auf Solid festgelegt werden. Damit kann noch immer ein Fluid modelliert werden, unter der Annahme, dass sich das Fluid nicht verformt.
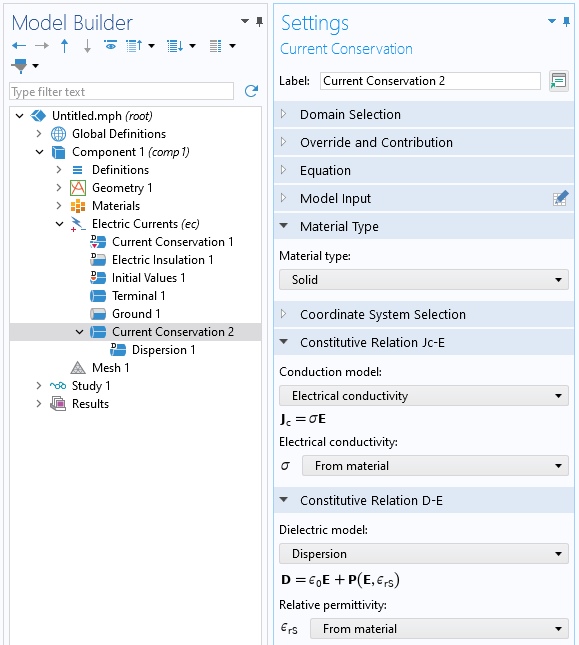
Das Feature Current Conservation, in dem das Modell Dispersion ausgewählt werden kann.
Nachdem Sie die Option Dielectric model auf Dispersion gesetzt haben, erscheint eine zusätzliche Unterfunktion. In diesem Feature werden die Zweige des Modells Multipole Debye und das Grenzverhalten eingegeben, wie im Screenshot unten gezeigt. Alternativ zur Eingabe der Pole oder Zweige ist es auch möglich, die Relaxationsdaten über das Modell Constant Loss Tangent anzugeben, das einen Verlusttangens, eine Mittenfrequenz und eine Bandbreite als Eingabe benötigt. Aus diesen Inputs bestimmt die Software automatisch die Anzahl der Pole, die Relaxationszeiten und die Beiträge zur relativen Permittivität. Es ist auch möglich, das einfachere Modell Debye zu verwenden, das einen einzigen Pol besitzt. Die thermischen Effekte, die eine Verschiebung der Relaxationszeiten verursachen, können optional in den Einstellungen Thermal Effects aktiviert werden.
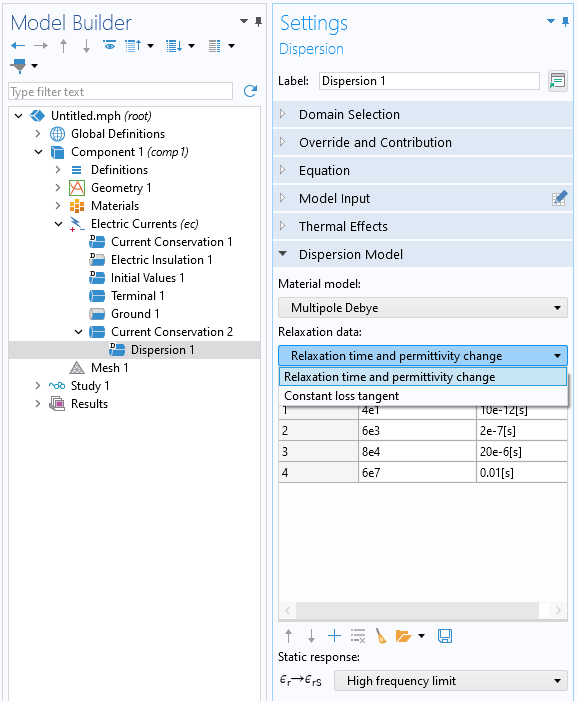
Die Unterfunktion Dispersion, in der die Zweige des Modells Multipole Debye eingegeben werden und das Grenzverhalten festgelegt wird.
Ein Blick auf die Ergebnisse
Wir können uns ansehen, wie sich die Dispersion auf die Reaktion eines einfachen Systems auswirkt, zum Beispiel eines Parallelplattenkondensators, der im Frequenzbereich arbeitet, und unsere beiden verschiedenen Materialien ausprobieren, die darin eingebettet sind. In den folgenden Plots können wir sehen, wie die Real- und Imaginärteile der Impedanz mit der Frequenz variieren.
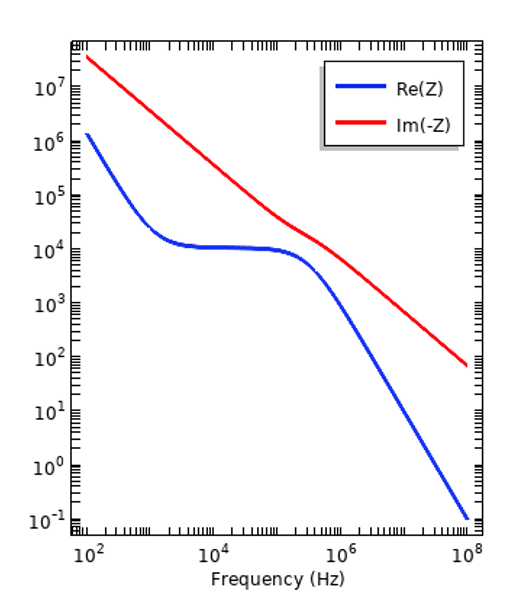
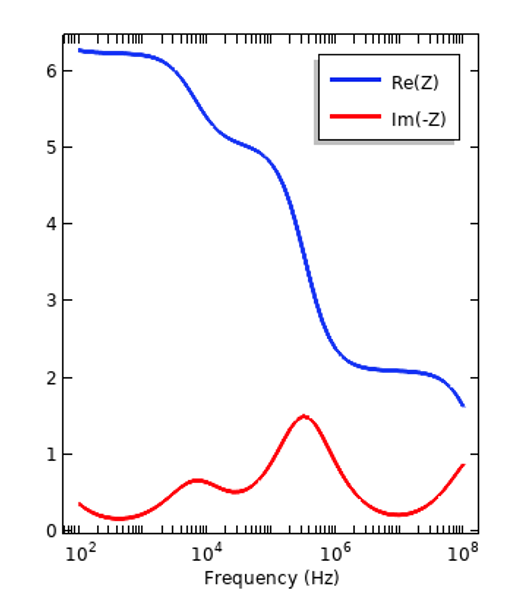
Impedanz eines Parallelplattenkondensators mit einer Probe eines Isolators (links) und einer Gewebeprobe (rechts) im Inneren. Beachten Sie, dass der negative Imaginärteil der Impedanz dargestellt ist.
Wir können das Modell auch verwenden, um die Ergebnisse einer Anregung desselben Systems im Zeitbereich zu erhalten. Wir werden dazu nur das Gewebematerial betrachten, in dem die Variation der Antwort über die Frequenz dramatischer ist. Der Aufbau des dispersiven Materials ist derselbe, aber es lohnt sich, die verschiedenen Möglichkeiten der Anregung eines solchen Systems zu untersuchen. Wir beginnen damit, das System mit einem geglätteten Stromsprung von 0-1A über 10 ns anzuregen und die Antwort über 100 µs zu berechnen, indem wir die am Anschluss gemessene Spannung aufzeichnen (siehe Abbildung unten). Die Ergebnisse werden über die Zeit und über die Zeit in logarithmischer Skala aufgetragen.
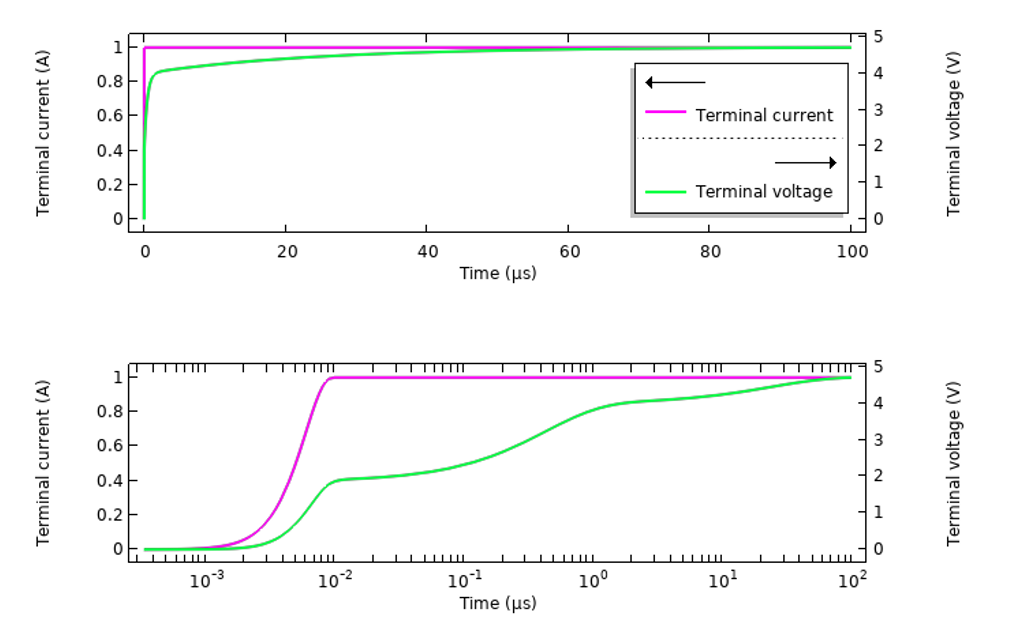
Die transiente Antwort des Gewebematerials auf einen aufgebrachten Strom über die Zeit.
Es ist interessant, diese Ergebnisse mit einem Modell zu vergleichen, das durch ein ähnlich glattes, gestuftes Spannungssignal angeregt wird, das sich entlang einer Übertragungsleitung ausbreitet. Die folgenden Abbildungen zeigen die Reaktion in Form von gemessenem Strom und Spannung. Beachten Sie, dass das hier aufgezeichnete Spannungssignal die Summe aus dem einfallenden geglätteten stufenförmigen Spannungssignal und dem von der Struktur und dem Material reflektierten Signal ist. Dieses Gesamtsignal weist aufgrund des dispersiven Materials ein zeitlich veränderliches Verhalten auf.
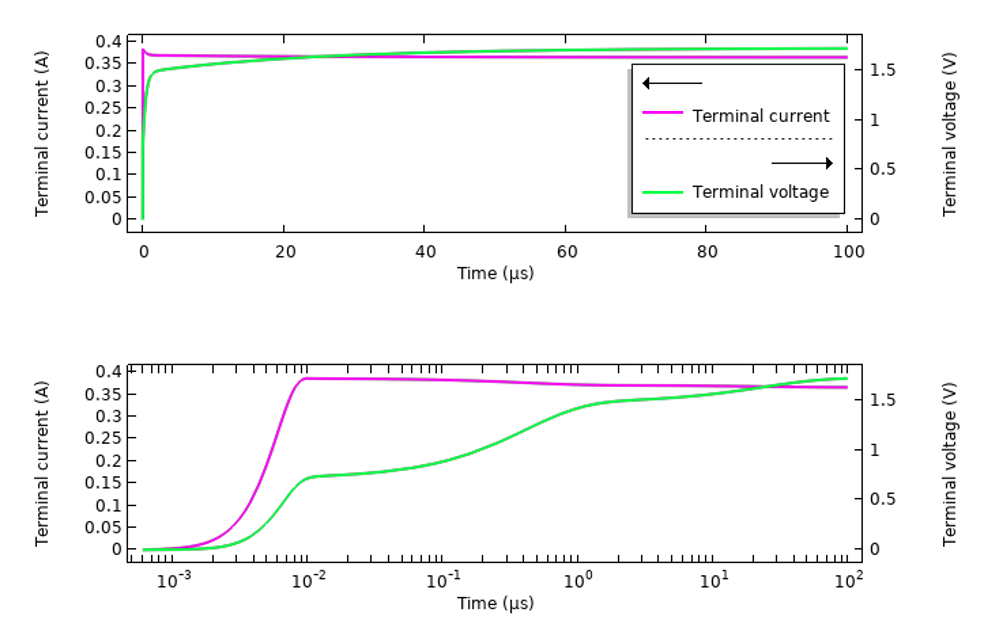
Die transiente Antwort der Gewebeprobe, die über eine Übertragungsleitung mit einem stufenförmigen Spannungssignal angeregt wird.
Abschließende Bemerkungen
Die Modellierung der elektrischen Dispersion ist jetzt mit dem Interface Electric Currents möglich und einfach einzurichten. Dieses Materialmodell vermittelt ein genaueres Bild der tatsächlichen elektrischen Antwort und der Verluste sowohl in Frequenz- als auch in Zeitbereichsmodellen. Diese Funktionalität ist für die Modellierung von vielen Materialien nützlich.
Es ist erwähnenswert, dass die Modellierung der elektrischen Dispersion seit Version 6.0 auch über das Interface Electrostatics möglich ist, in dem sie in erster Linie für die Modellierung von verlustbehafteten piezoelektrischen Materialien vorgesehen ist. Das RF Module und das Wave Optics Module enthalten zudem weitere Dispersionsmodelle für die Modellierung bei viel höheren Frequenzen.



Kommentare (0)