Modellierung der Erzeugung akustischer Energie in thermoakustischen Motoren

Thermoakustische Motoren erzeugen akustische Energie aus Wärme. Im Gegensatz zu häufig verwendeten Motoren wie Hubkolbenmotoren und Gasturbinen verwenden thermoakustische Motoren keine beweglichen Teile, wodurch ihre Struktur sehr einfach bleibt. In diesem Blog-Beitrag werden wir sehen, wie die Funktionsweise von thermoakustischen Motoren mit dem Interface Thermoviscous Acoustics modelliert werden kann, einem leistungsfähigen Interface der Software COMSOL Multiphysics^® zur Modellierung des linearisierten Verhaltens eines Fluids.

Wie funktionieren thermoakustische Motoren?

Vor mehr als 150 Jahren berichtete Professor Pieter Rijke über ein interessantes Phänomen, das als Pionierarbeit auf dem Gebiet der Thermoakustik angesehen werden kann. Er steckte Drahtnetz in einen senkrecht gehaltenen Glaszylinder und erhitzte das Netz von unten mithilfe von Feuer. Nachdem er das Feuer gelöscht hatte, stellte er fest, dass der Zylinder noch eine Weile lang Töne erzeugte. (Ref. 1) Der Apparat ist heute unter dem Namen Rijke-Rohr bekannt, so dass einige ihn vielleicht als Beispiel für ein Resonanzphänomen kennen. Aber von der Resonanz mal abgesehen, wie entstehen die Töne?

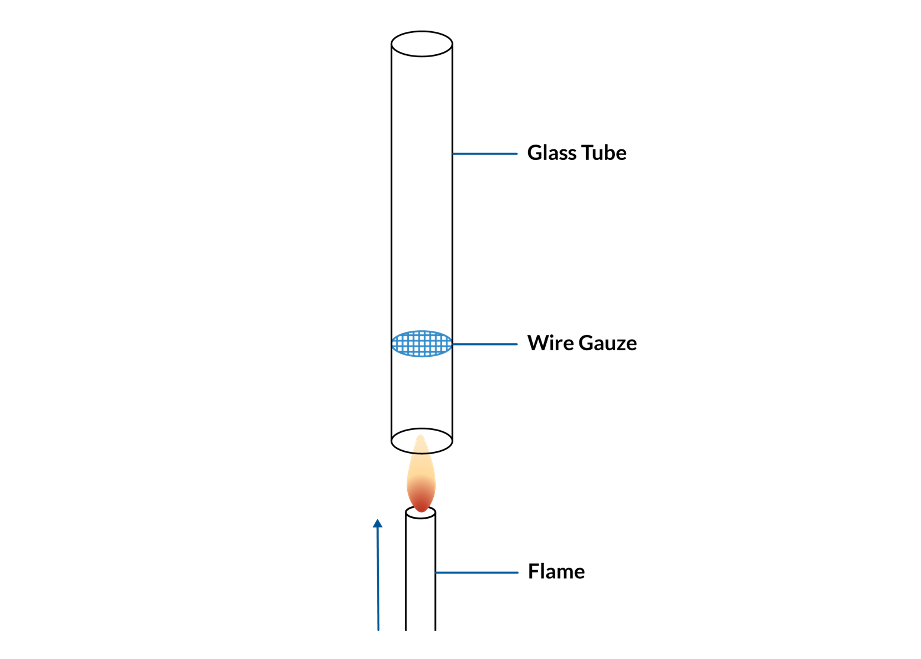
Der Aufbau des Rijke-Rohrs.

Der Trick ist die Wechselwirkung zwischen der Temperaturänderung und der Bewegung des Fluids im Inneren des Rohrs: Das beheizte Drahtnetz induziert eine natürliche Konvektion der Luft, wodurch eine gleichmäßige Strömung durch das Rohr entsteht; die Luft über dem Drahtnetz ist also wärmer als die Luft unter dem Drahtnetz. Bei der stehenden akustischen Halbwellenresonanz im Rohr strömt die Luft zu unterschiedlichen Zeiten in der akustischen Periode in beide Richtungen durch das Drahtnetz. Wenn die Luft durch das Netz strömt, wird sie erwärmt. Da die Luft unter dem Netz kälter ist als die Luft darüber, wird mehr Wärme übertragen, wenn die Strömung nach oben und nicht nach unten gerichtet ist. Um ein anhaltendes akustisches Feld zu erhalten, muss die Wärmeabgabe in Phase mit dem Druckfeld sein, so dass das Fluid erwärmt wird, wenn der akustische Druck positiv ist. Bei einer stehenden Welle ist das Geschwindigkeitsfeld, das die Erwärmung verursacht, nicht in Phase mit dem Druckfeld. Aufgrund von Effekten, die durch die viskosen Randschichten, die das Drahtnetz umgeben, verursacht werden, ist die Wärmeabgabe jedoch im Vergleich zum Geschwindigkeitsfeld verzögert. Diese Phasenverzögerung bewirkt, dass die Wärmeabgabe teilweise in Phase mit dem Druckfeld ist und zu einer anhaltenden Resonanz führt. Wenn das Rohr auf die Seite gedreht wird, hört die Konvektion auf und die Resonanz wird nicht mehr aufrechterhalten. Wenn das Rohr auf den Kopf gestellt wird, ist der Wärmetransport am größten, wenn der Schalldruck negativ ist, daher wird das Schallfeld abgeschwächt.

Dies ist ein Beispiel für die Energieumwandlung zwischen Wärme und akustischer Energie. Der Apparat demonstriert auch die Funktionsweise von thermoakustischen Motoren.

Thermoakustische Motoren haben einen geschlossenen, röhrenförmigen Kanal, in dem sich der Schall ausbreiten kann. In diesem Kanal befindet sich ein Wärmetauscher, der das Fluid erhitzt oder kühlt. Thermoakustische Motoren verwenden entweder stehende Wellen oder fortschreitende Wellen, während das Rijke-Rohr nur stehende Wellen nutzt. Es ist zu erwarten, dass Motoren mit fortschreitenden Wellen aufgrund der Phasenverzögerung zwischen dem Druck und der Verdrängung des Fluids eine bessere Leistung erzielen als Motoren mit stehenden Wellen. In diesem Blog-Beitrag werden wir uns hauptsächlich mit Modellen von Motoren mit fortschreitenden Wellen befassen.

Lassen Sie uns über das Prinzip von thermoakustischen Motoren nachdenken, die mit fortschreitenden Wellen arbeiten. Um die Welle zu verstehen, sehen Sie sich die Bewegung der kleinen Fluidpakete in der Abbildung unten an. Schallwellen sind Longitudinalwellen. Wenn also eine Welle mit hohem Druck von links kommt, werden die Pakete nach rechts geschoben. Wenn eine Welle mit niedrigem Druck von links auf ein Fluidpaket trifft, wird das Paket nach links gezogen.

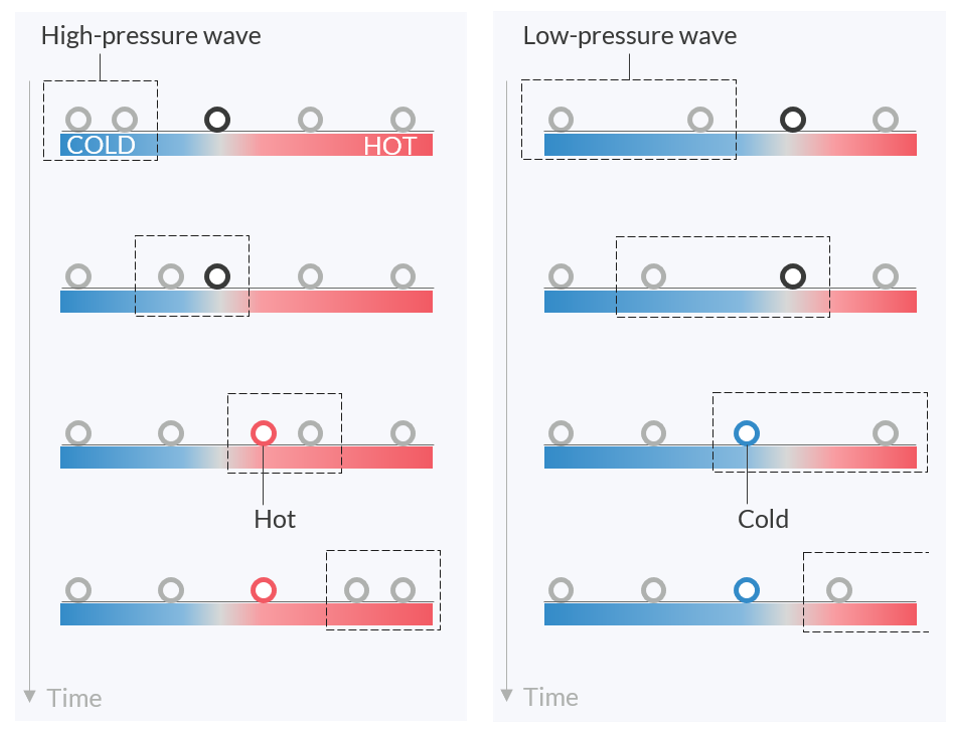
Wie sich Pakete in einem Fluid unter einer von links kommenden Welle bewegen. Ein imaginärer Bereich der Welle wird durch einen gepunkteten Kasten dargestellt. Bei einem entsprechenden Temperaturgefälle in der benachbarten Platte wird sich das Paket immer in den heißeren Bereich bewegen, wenn es von einer Welle mit hohem Druck angestoßen wird, und in den kälteren Bereich, wenn es von einer Welle mit niedrigem Druck angezogen wird.

Als nächstes können Sie eine beheizte Platte entlang des Weges der Welle in die Röhre legen. Wenn das rechte Ende der Platte beheizt wird, während das linke Ende auf einer moderaten Temperatur gehalten wird, entsteht ein Temperaturgefälle in der Platte. Der Temperaturgradient heizt die Pakete auf, wenn sie sich nach rechts bewegen, und er absorbiert die Wärme, wenn sie sich nach links bewegen. Da der Druck eines Pakets am höchsten ist, wenn es sich nach rechts bewegt, wird durch die Erwärmung des Pakets der Höchstwert des Drucks nach oben gedrückt. Auf die gleiche Weise verringert die Wärmeabsorption, wenn sich ein Paket nach links bewegt, auch den Mindestdruck. Dieses periodische Auf und Ab der Temperatur synchronisiert die Bewegung der Pakete und erhöht schließlich die Amplitude der Welle. Alle Pakete arbeiten wie eine Kette zusammen, um die Druckwelle weiterzuleiten und der Welle durch den Austausch von Wärme Energie zuzuführen. Beachten Sie, dass der Temperaturgradient in der Platte in dieselbe Richtung gehen sollte wie die Wellenausbreitung, andernfalls wird die Welle abgeschwächt.

Wenn Sie sich fragen, man den Zyklus auch umkehren kann, lautet die Antwort Ja. Ein solches System wird thermoakustische Wärmepumpe oder thermoakustischer Kühlschrank genannt und kann mithilfe von Schallwellen Wärme transportieren. Das Funktionsprinzip ist einfach: Wenn eine Welle mit hohem Druck auf ein Paket trifft, wird das Paket komprimiert, die Temperatur steigt folglich an und das Paket beginnt, seine Wärme an das benachbarte Objekt abzugeben, während es sich nach rechts bewegt. Umgekehrt nimmt ein Paket bei einer Welle mit niedrigem Druck Wärme auf und bewegt sich nach links.

Die Erklärung in diesem Blog-Beitrag dient nur der Einführung und enthält nicht alle Details zu thermoakustischen Motoren. Wenn Sie an detaillierteren Informationen über thermoakustische Motoren interessiert sind, lesen Sie Ref. 2.

Linearisierte Gleichungen für die Modellierung der Thermoakustik

Es ist immer eine wichtige Überlegung, welche Gleichungen und welches Interface für eine neue Simulation geeignet sind. Für das vorliegende Modellierungsbeispiel liegt die Verwendung des Acoustics Module nahe, um die thermoakustische Schwingung zu simulieren, da das Phänomen mit akustischen Wellen zusammenhängt. Da das akademische Gebiet Thermoakustik genannt wird, scheint das Interface Thermoviscous Acoustics eine gute Wahl zu sein. Sehen wir uns die Gleichungen und die Fähigkeiten dieses Interfaces an, um unsere Auswahl zu bestätigen.

Das Interface Thermoviscous Acoustics verwendet in einer Zeitbereichsanalyse die folgenden Gleichungen:

 
wobei \rho, \bm{u}, T und p jeweils Dichte, Geschwindigkeit, Temperatur und Druck sind. Der tiefgestellte Index {\cdot}_0 drückt aus, dass der Wert zur mittleren Hintergrundströmung gehört, während die Variablen mit dem tiefgestellten Index {\cdot}_t die akustischen Störungen darstellen. Die maßgeblichen Gleichungen des Interface Thermoviscous Acoustics werden von den Navier-Stokes-Gleichungen (den exakten Gleichungen der Fluidbewegung) abgeleitet, die auf der Annahme beruhen, dass jeder Störungsterm zweiter Ordnung in der Simulation weggelassen werden kann und dass die Geschwindigkeit der mittleren Hintergrundströmung Null ist (\bm{u}_0=\bm{0}).

Wir müssen darauf achten, welche Nichtlinearitäten vernachlässigt werden, und ob die linearisierten Gleichungen das Phänomen abdecken, das uns interessiert. Bei thermoakustischen Motoren wird der Wärmeaustausch zwischen einem Fluid und einem Wärmetauscher durch den Diffusionsterm \nabla \cdot (k\nabla T_{\rm t}) ausgedrückt, und der Wärmetransport aufgrund der akustischen Schwingung wird durch den linearisierten Advektionsterm \bm{u}_{\rm t}\cdot \nabla T_0 ausgedrückt. Ein kaltes Fluid mit hohem Druck, das durch den Term \bm{u}_{\rm t}\cdot \nabla T_0 einströmt, wird in einem Wärmetauscher durch \nabla \cdot (k\nabla T_{\rm t}) erwärmt, und die Energie wird durch die dritte Gleichung erhöht. Diese Terme beschreiben die wichtigen Mechanismen des Wärmetransports in unserem System, und daher scheinen die linearisierten Gleichungen gut für die Modellierung des Motors geeignet zu sein.

Beachten Sie auch, dass es keinen Advektionsterm gibt, der für die Kopplung des zeitlich veränderlichen Temperaturfeldes und der Oszillationsgeschwindigkeit, \bm{u}_{\rm t}\cdot\nabla T_t, steht. Diese gekoppelte Darstellung würde den durch die Oszillation verursachten Transport des transienten Temperaturfeldes zeigen. Der Advektionsterm ist wichtig für die Simulation von Wärmepumpen, bei denen der Temperaturgradient im Gleichgewicht als Ergebnis von Oszillationen bestimmt wird und nicht a priori verfügbar ist. In solchen Fällen können wir das Feature Nonlinear Thermoviscous Acoustics Contributions verwenden, das es dem Modell ermöglicht, die nichtlinearen Terme im Interface Thermoviscous Acoustics, Transient zu berücksichtigen. Die Simulation von Nichtlinearitäten kann kostspielig sein, daher sollte die nichtlineare Funktionalität nur in den relevanten Gebieten hinzugefügt werden.

Modellierung in COMSOL Multiphysics^®

Bisher haben wir uns mit den grundlegenden Funktionsmechanismen thermoakustischer Motoren und den entsprechenden Gleichungen für ihre Modellierung befasst, so dass wir nun mit dem Aufbau der Modelle beginnen können. Sie können die Modelldateien für die hier gezeigten Beispiele in der Application Gallery aufrufen. Wie im vorigen Abschnitt besprochen, verwenden wir das Interface Thermoviscous Acoustics, um thermoakustische Motoren zu modellieren. Da das stationäre Hintergrundtemperaturfeld nicht einheitlich ist, verwenden wir außerdem das Interface Heat Transfer. Anstatt die beiden Interfaces gleichzeitig zu verwenden, kann die Studie in zwei Studienschritte aufgeteilt werden: einen Schritt Stationary für das Hintergrund-Temperaturfeld und einen Schritt Time Dependent für die akustischen Felder. Die Kopplung erfolgt dadurch, dass die Lösung des Interface Heat Transfer als Gleichgewichtstemperatur im Knoten Thermoviscous Acoustics Model festgelegt wird.

Was die Randbedingungen des Interface Thermoviscous Acoustics betrifft, sollten wir die Wand des Wärmetauschers als isotherm (T_{\rm t} = 0) festlegen. Diese Bedingung heizt die Temperatur des Fluids bei hohem Druck auf (wo T_{\rm t} aufgrund der Advektion aus dem kühleren Bereich kleiner als Null ist) und kühlt das Fluid ab, wenn sein Druck niedrig ist (wo T_{\rm t} größer als Null ist).

Beispiel 1: Einfacher Kreislauf

Zunächst werden wir einen Motor modellieren, der aus einem einfachen Kreislauf besteht. Er hat einen Wärmetauscher im rechten Kanal und der gesamte Kanal bildet einen geschlossenen Kreislauf. Die stationäre Temperatur ist in der Abbildung unten dargestellt. Der Temperaturgradient im unteren Bereich des Wärmetauschers ist auffällig, aber unser Augenmerk liegt auf dem Temperaturgradienten in den kleinen Zwischenräumen des Wärmetauschers.

Die Gleichgewichtstemperatur in einem einfachen kreisförmigen Motor (links: komplettes System; rechts: Detailansicht um den Wärmetauscher). Das untere Ende der engen Passagen in einem Wärmetauscher wird auf 493 K erhitzt.

Im Studienschritt Time Dependent wird eine stehende Welle als Anfangsbedingung für den Druck vorgegeben, damit sie die Oszillation innerhalb des Kreislaufs auslösen kann. Im weiteren Verlauf der Simulation wächst die Amplitude, wie das Feature Point Probe zeigt (siehe unten). Es ist klar, dass die Oszillation immer größer wird, was bedeutet, dass die thermische Energie in akustische Energie umgewandelt wird.

Das Feature Point Probe ist so eingestellt, dass der Druck im Motor verfolgt wird. Die Druckdaten werden an einem Punkt im Wärmetauscher erfasst, der sich in der Nähe des Druckknotens der stehenden Welle befindet, die als Ausgangsdruckverteilung verwendet wird.

Wie sieht also der Druck im Motor aus? Die drei folgenden Abbildungen veranschaulichen die Druckverteilung bei t = 0,281 s, 0,285 s bzw. 0,289 s. Bei t = 0 s besteht eine stehende Welle, aber nach kurzer Zeit beginnt die Verteilung im Uhrzeigersinn zu rotieren. Die Welle bewegt sich in die gleiche Richtung wie der Temperaturgradient im Wärmetauscher, und die gegen den Uhrzeigersinn gerichtete Komponente der anfänglichen stehenden Welle schwächt sich ab, da ihr keine Energie zugeführt wird. Interessanterweise kann die Anregung einer Welle gegen den Uhrzeigersinn simuliert werden, indem man die Richtung des Temperaturgradienten in der Mitte der Simulation umdreht. In der Modelldatei wird der Studienschritt Stationary erneut mit dem umgekehrten Temperaturprofil bei t = 0,3 s berechnet, und der Studienschritt Time Dependent spiegelt die Veränderung der Gleichgewichtstemperatur seit diesem Zeitpunkt wider. Die Welle im Uhrzeigersinn bleibt bis etwa t = 0,6 s bestehen. Danach entsteht eine stehende Welle und schließlich breitet sich die Welle gegen den Uhrzeigersinn aus.

Verlauf der Druckverteilung (links: t = 0.281 s; Mitte: t = 0.285 s; rechts: t = 0.289 s). Sowohl der Hochdruckbereich als auch der Niederdruckbereich bewegen sich aufgrund des bereits erwähnten thermoakustischen Effekts im Uhrzeigersinn.

Beispiel 2: Kreislauf mit einer Verzweigung

Zusätzlich zu dem einfachen Kreislauf werden wir eine weitere Konfiguration untersuchen. Die folgende Abbildung zeigt das nächste Modellbeispiel mit einer komplexen Geometrie. Die Geometrie imitiert den Versuchsaufbau in Ref. 3. Das Modell ist 2D und vereinfacht, um den gleichen hydraulischen Durchmesser zu erreichen wie der in der Referenz beschriebene Wärmetauscher. Das verzweigte Rohr am unteren rechten Ende dient der späteren Extraktion der Schallenergie. Wie in Beispiel 1 wird der Kreislauf im Motor verwendet, um thermische Energie in akustische Energie umzuwandeln, aber hier kann ein Teil der Energie an der Verzweigung entnommen werden.

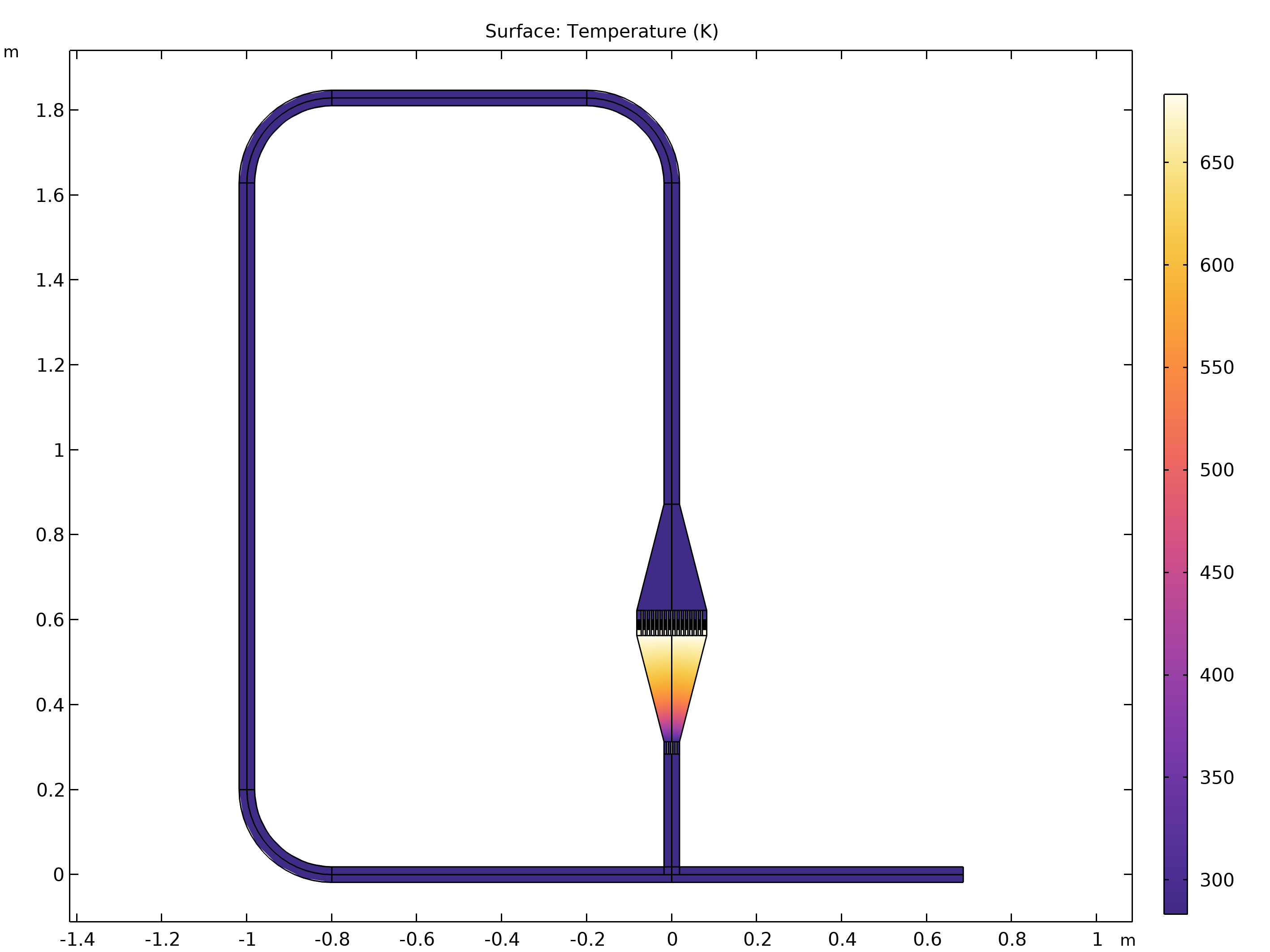
Die Gleichgewichtstemperatur in einem Modell mit einer Verzweigung. Die Geometrie imitiert den experimentellen Aufbau in Ref. 3.

Die momentanen Druckverteilungen im Motor sind in der folgenden Abbildung dargestellt. Dort, wo die Bogenlänge 3,6 m beträgt, gibt es einen starken Abfall, der durch den viskosen Widerstand in den kleinen Lücken am Wärmetauscher verursacht wird. Bemerkenswert ist, dass die Amplitude des Drucks stark von der Position abhängig ist. Dies ist auf die Komplexität des Modells zurückzuführen, wie zum Beispiel den viskosen Luftwiderstand und eine stehende Wellenkomponente, die im Motor auftritt. In der Abbildung ist auch der zeitliche Maximalwert des absoluten Drucks, bezeichnet als max(|p|), für jede Position dargestellt. Beachten Sie, dass die Amplitude zwar etwas groß erscheint, dass aber bei dieser Simulation davon ausgegangen wird, dass es keine Turbulenzen gibt und dass jede Störung linear ist. Die Verteilung der ungefähren Amplitude, max(|p|), stimmt gut mit den experimentellen und analytischen Daten in Ref. 3 überein.

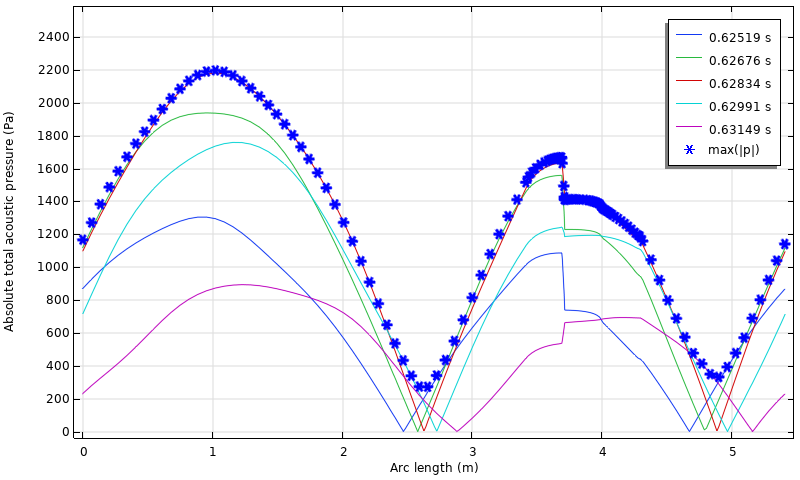
Momentane Druckverteilungen entlang des Kreislaufs und die angenäherte Amplitude, max(|p|), die durch eine Zustandsvariable berechnet wird.

Weitere Beispiele

Seit der Demonstration von Professor Rijke hat das Verständnis der Thermoakustik erheblich zugenommen, und ihre Anwendung in Energiegeräten wird nun aktiv erforscht. In diesem Blog-Beitrag haben wir uns damit beschäftigt, wie thermoakustische Motoren mit dem Interface Thermoviscous Acoustics modelliert werden können, und die interessanten Eigenschaften der Motoren visualisiert.

In der Application Gallery finden Sie viele Modelle aus verschiedenen physikalischen Disziplinen. Zwei Modelle beziehen sich auf die Thermoakustik:

• Simple Thermoacoustic Engine ist ein Modell eines thermoakustischen Motors mit stehender Welle. Es gibt mehrere Modelldateien, die einen Vergleich der Erstellung desselben Modells mit zwei verschiedenen Ansätzen ermöglichen: ein linearer Störungsansatz durch das Interface Thermoviscous Acoustics, Transient und ein vollständig nichtlinearer Ansatz durch das Multiphysik-Interface Nonisothermal Flow. Der letztere Ansatz löst die Navier–Stokes-Gleichungen und berücksichtigt die Nichtlinearität auf Kosten einer erhöhten Rechenzeit.
• Thermoacoustic Engine and Heat Pump ist ein Modell einer Wärmepumpe mit stehender Welle. Im Gegensatz zu thermoakustischen Motoren erfordert die Simulation von thermoakustischen Wärmepumpen die Berechnung des nichtlinearen Advektionsterms \bm{u_t}\cdot\nabla T_{\rm t}, da die Temperatur aufgrund des thermischen Transporteffekts immer weiter abnimmt. In dem Modell wird der Knoten Nonlinear Thermoviscous Acoustics Contributions zum Interface Thermoviscous Acoustics hinzugefügt, um die Nichtlinearität zu berücksichtigen. Das Modell verwendet auch die Kopplung Thermoviscous Acoustic-Thermal Perturbation Boundary, ein neues Feature in Version 6.2. Die Kopplung wird verwendet, um den Wärmeaustausch zwischen dem oszillierenden Fluid und den festen Platten im Durchgang zu simulieren, da die Temperatur des Festkörpers mit dem Abpumpen der Wärme immer weiter abnimmt.

Referenzen

1. P.L. Rijke, “LXXI. Notice of a new method of causing a vibration of the air contained in a tube open at both ends,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 17, no. 116, 419–422, 1859; https://doi.org/10.1080/14786445908642701
2. G.W. Swift, Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators, Springer, 2017; https://doi.org/10.1007/978-3-319-66933-5
3. M. McGaughy et al., “A Traveling Wave Thermoacoustic Engine—Design and Test,” Letters Dyn. Sys. Control, vol. 1, no. 3, July 2021; https://doi.org/10.1115/1.4049528