
In Ihren Finite-Elemente-Modellen werden Sie das Konzept der numerischen Integration und der Gauß-Punkte in verschiedenen Zusammenhängen antreffen. In diesem Blog-Beitrag gehen wir darauf ein, wo und warum die numerische Integration verwendet wird. Außerdem werden die Möglichkeiten aufgezeigt, die Sie haben, um die numerischen Integrationsschemata in der COMSOL Multiphysics® Software zu überprüfen und zu ändern. Schließlich wird die Verwendung von Gauß-Punkt-Freiheitsgraden erläutert.
Inhaltsverzeichnis
- Was ist numerische Integration?
- Integration der schwachen Beiträge
- Modifikation der Integrationsordnung
- Integrierte reduzierte Integration
- Integrations-Kopplungsoperatoren
- Integration während des Postprocessings
- Gauß-Punkt-Formfunktionen
- Der Operator gpeval
Was ist numerische Integration?
Bei der Berechnung von Integralen nicht trivialer Funktionen über allgemeine Gebiete müssen wir auf numerische Methoden zurückgreifen. Numerische Integration wird auch als numerische Quadratur bezeichnet. Die Idee dahinter ist, dass das Integral durch eine Summe ersetzt wird, wobei der Integrand aus einer Reihe von diskreten Punkten gesampelt wird. Dies kann wie folgt beschrieben werden:
wobei xi die Positionen der Integrationspunkte und wi die entsprechenden Gewichtungsfaktoren sind. Die Integrationspunkte werden oft als Gauß-Punkte bezeichnet, obwohl diese Nomenklatur streng genommen nur für Integrationspunkte korrekt ist, die durch die Gaußsche Quadraturmethode definiert sind. In COMSOL Multiphysics wird die echte Gaußsche Quadratur für die Integration in 1D, viereckige Elemente in 2D und hexaedrische Elemente in 3D verwendet. Andere, ähnliche Schemata werden für andere Elementgeometrien verwendet.
Gaußsche Quadratur
Beim Algorithmus der Gaußschen Quadratur werden die Positionen der Integrationspunkte und ihre Gewichte so gewählt, dass ein Polynom möglichst hohen Grades exakt integriert werden kann. Da ein Polynom vom Grad N N+1 Koeffizienten enthält und eine Gaußsche Punktregel mit M Punkten 2M Parameter (Positionen + Gewichte) enthält, ist die höchste Ordnung des Polynoms, die exakt integriert werden kann, N = 2M – 1.
Die Gaußsche Quadratur ist sehr effizient für die Integration von Feldern, die durch ein Polynom eines bestimmten Grades gut angenähert werden können. Die Integrationspunkte und Gewichte für die ersten Ordnungen der Gaußschen Quadratur in 1D sind in der folgenden Tabelle aufgeführt. Das Integral wird über das normalisierte Intervall [-1,1] gebildet.
| Ordnung (M) | Genauigkeit (N) | Position (xi) | Gewichte (wi) |
|---|---|---|---|
| 1 | 1 | 0 | 2 |
| 2 | 3 | ±0.577 | 1 |
| 3 | 5 | 0, ±0.775 | 0.889 (= 8/9), 0.556 (= 5/9) |
| 4 | 7 | ±0.340, ±0.861 | 0.652, 0.348 |
| 5 | 9 | 0, ±0.538, ±0.906 | 0.569, 0.479, 0.237 |
In COMSOL Multiphysics werden die Integrationsordnungen durch den Grad des Polynoms bezeichnet, das genau integriert werden kann. Es werden nur gerade Zahlen verwendet. Bei der echten Gauß-Punkt-Integration ist die Genauigkeit, wie oben gezeigt, immer eine ungerade Potenz. Die von der Software als “4” bezeichnete Integrationsordnung hat bei den Elementformen, bei denen die Gaußsche Quadratur verwendet wird, tatsächlich die Genauigkeit 5.
Beispiele für die Gaußsche Quadratur
Als Beispiel für eine Gaußsche Quadratur betrachten wir die Funktion
Über dem Quadrat -1 ≤ x ≤ 1, -1 ≤ y ≤ 1 ist das Integral dieser Funktion 1. Wie in der Abbildung unten zu sehen ist, hat die Funktion eine komplexe Verteilung über das Gebiet.
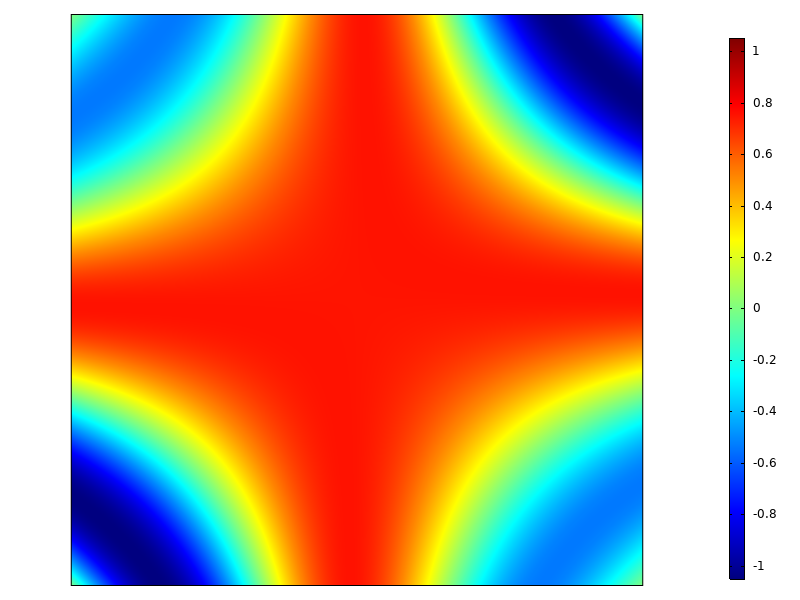
Die zu integrierende Funktion.
In der folgenden Tabelle sind die Ergebnisse verschiedener Gaußscher Quadraturordnungen dargestellt. Sobald die Funktion durch ein Polynom eines bestimmten Grades vernünftig angenähert werden kann, konvergiert der Wert des Integrals schnell.
| Integrations- punkte |
Genauigkeit | Integrations- ordnung |
Wert | Kommentare |
|---|---|---|---|---|
| 1 | 1 | 0 (or 1) | 2.9958 | Wenn nur der Wert am Schwerpunkt verwendet wird, wird das Integral deutlich überschätzt |
| 2×2 | 3 | 2 (or 3) | 0 | Bei der 2×2-Regel befinden sich die Gauß-Punkte bei pm \frac{1}{\sqrt{3}}, wo die Kosinusfunktion 0 ist (Pech!) |
| 3×3 | 5 | 4 (or 5) | 1.1519 | |
| 4×4 | 7 | 6 (or 7) | 0.9887 | |
| 5×5 | 9 | 8 (or 9) | 1.0005 | |
| 6×6 | 11 | 10 (or 11) | 1.0000 | |
| 7×7 | 13 | 12 (or 13) | 1.0000 | |
| 8×8 | 15 | 14 (or 15) | 1.0000 |
Das optimale Verhalten der Gaußschen Quadratur für Polynome hat jedoch auch einen Nachteil: Die Methode ist nicht sehr gut für die Integration stark diskontinuierlicher Funktionen geeignet. Nehmen wir an, wir wollen eine Funktion, die f(x,y) = 1 ist, wenn y < -2x – 1 und 0 anderswo, über das gleiche Quadrat wie oben integrieren. Da die Funktion auf einem Viertel des Quadrats den Wert 1 hat und das Quadrat den Flächeninhalt 4 hat, können wir sofort sehen, dass das exakte Integral 1 ergeben sollte. Die Ergebnisse sind in der folgenden Tabelle aufgeführt.
| Integrationspunkte | Wert | Kommentare |
|---|---|---|
| 1 | 0 | Nur ein Punkt bei (0,0), an dem die Funktion den Wert 0 hat |
| 2×2 | 1 | Einer der vier Punkte hat den Wert 1 und sein Gewicht ist 1 |
| 3×3 | 0.8025 | Zwei Punkte erhalten den Wert 1, und ihre Gewichte sind \frac{25}{81}, \frac{40}{81} |
| 4×4 | 1.2269 | Fünf Punkte erhalten den Wert 1 |
| 5×5 | 1.0325 | |
| 6×6 | 1.0918 | |
| 7×7 | 0.9892 | |
| 8×8 | 0.9961 |

Der Fall mit 4×4 Integrationspunkten. Die orangefarbene Fläche ist die, in der die Funktion den Wert 1 hat, und die grünen Gauß-Punkte sind diejenigen, die zum Wert des Integrals beitragen.
Wie Sie in der Tabelle sehen können, ist der Aufwand für die Berechnung eines genauen Integrals dieser unstetigen Funktion erheblich. Rein zufällig liefert das 2×2-Integrationsschema die genaue Antwort, aber die Konvergenz ist alles andere als monoton.
Warum ist das wichtig? Bei der Finite-Elemente-Analyse können Sie auf Felder stoßen, die scharfe lokale Gradienten aufweisen. Einige Beispiele sind Probleme mit Phasenübergängen oder beim Einsetzen der Plastizität in der Festkörpermechanik. Integrale, die über Elemente mit derartigen Sprüngen berechnet werden, können erhebliche Diskretisierungsfehler aufweisen. Auch die Konvergenz der Lösung kann beeinträchtigt werden. Kleine Änderungen in der Lösung können die berechneten Residuen erheblich verändern, wenn einzelne Gauß-Punkte ihren Zustand ändern.
In solchen Fällen kann es besser sein, eine niedrigere Polynomordnung als die Standardeinstellung für die Formfunktionen zu wählen, die zur Diskretisierung des Feldes verwendet werden. Die geringere Auflösung kann durch die Verwendung eines dichteren Netzes kompensiert werden. Der Effekt ist, dass die unvermeidlichen Sprünge auf kleinere Elemente mit weniger Integrationspunkten begrenzt werden.
Wenn Sie beim Postprocessing Integrale von diskontinuierlichen Funktionen berechnen, müssen Sie außerdem die potenziell langsame Konvergenz der numerischen Integration berücksichtigen.
Integration der schwachen Beiträge
Innerhalb jedes finiten Elements gibt es verschiedene Ausdrücke, die integriert werden müssen, um z.B. Steifigkeitsmatrizen, Massenmatrizen, Lastvektoren und Residuen zu bilden. Am Beispiel der Festkörpermechanik entspricht die schwache (oder Variations-) Standardformulierung dem Prinzip der virtuellen Arbeit: Die virtuelle Arbeit, die von den inneren Spannungen geleistet wird, die auf eine virtuelle Dehnungsänderung wirken, ist gleich der virtuellen Arbeit, die von den äußeren Kräften geleistet wird, die auf die entsprechende virtuelle Änderung der Verschiebungen wirken.
Hier steht die Tilde (~) für die virtuelle Variation. In einem Ausdruck in COMSOL Multiphysics wird dies durch den Operator test() dargestellt. Volumenkräfte, f, und Randzugkräfte, t, sind hier enthalten, aber es können auch andere Arten von Beiträgen auftreten. Die linke Seite trägt zur Steifigkeitsmatrix bei, während die rechte Seite zum Lastvektor beiträgt (unter der Annahme, dass die Kräfte unabhängig von den Verschiebungen sind).
Um die Formulierungen der Finite-Elemente-Implementierungen in COMSOL Multiphysics zu überprüfen, müssen Sie den Equation View aktiviert haben.
Aktivierung des Equation View.
Wenn wir uns im Equation View unter einem Materialmodell (z.B. Linear Elastic Material) im Interface Solid Mechanics umsehen, gibt es einen Abschnitt namens Weak Expressions. Dort sehen Sie die Ausdrücke, die zur Bildung verschiedener Matrizen verwendet werden, zum Beispiel der Steifigkeitsmatrix.
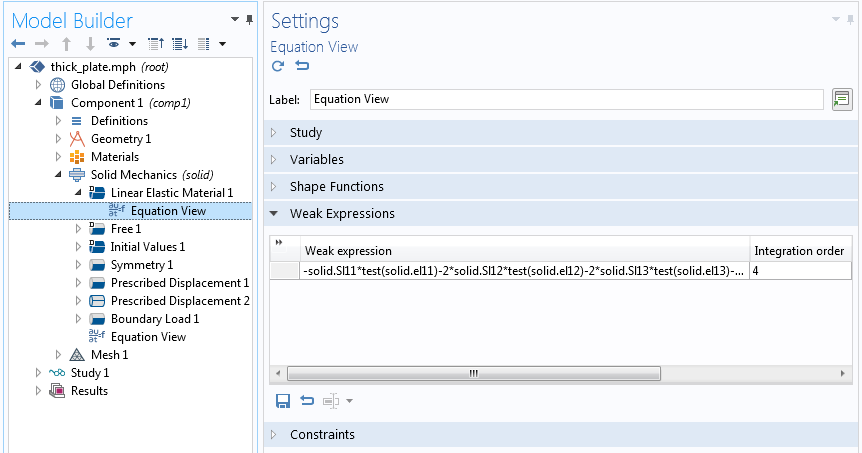
Inspektion des schwachen Ausdrucks in Linear Elastic Material im Interface Solid Mechanics in einem stationären Fall.
In der obigen Abbildung sehen Sie ein Textfeld für die Integrationsordnung, die in diesem Fall den Wert 4 hat. Die Zahl, die die Integrationsordnung in COMSOL Multiphysics beschreibt, ist die höchste Ordnung des Polynoms, die exakt integriert werden kann. Die Standardintegrationsordnung basiert auf der Ordnung der Formfunktionen, die zur Beschreibung des Feldes (in diesem Fall der Verschiebungen) verwendet werden. Hier wird die Standardordnung der Formfunktionen – quadratisch – verwendet, so dass die Spannungen und Dehnungen im Wesentlichen eine lineare Variation über das Element haben werden. Das Produkt aus Spannungs- und Dehnungsvariation ist also quadratisch, was darauf hindeutet, dass die Ordnung 4 mehr als notwendig sein könnte. Warum dieser Wert gewählt wurde, erläutern wir weiter unten.
Lassen Sie uns als zweites Beispiel eine Randlast in Solid Mechanics untersuchen.
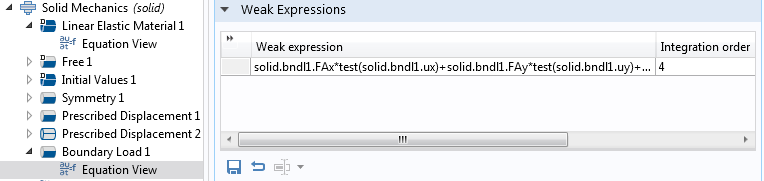
Der schwache Ausdruck für das Feature Boundary Load.
Auch hier ist die Integrationsordnung 4. Da die Formfunktionen der Verschiebung quadratische Polynome sind, bedeutet dies, dass es möglich sein sollte, einen Lastbeitrag genau zu integrieren, für den die Zugkraft nicht mehr als eine quadratische Variation hat, da das Produkt aus Zugkraft und Variation der Verschiebung dann die Ordnung 4 hat.
Einige Feinheiten der schwachen Ausdrücke
Die obige Diskussion gilt streng genommen nur, wenn die Elemente ideale Formen haben (z.B. keine gekrümmten Ränder). Wenn Sie sich näher mit der Theorie befassen, enthalten die Integrale tatsächlich auch einen lokalen Skalierungsfaktor (Jacobi), der sich aus der Transformation zwischen der tatsächlichen Elementgeometrie und der nominalen Elementgeometrie ergibt. Wenn zum Beispiel ein Integral über ein 2D-Viereckselement durchgeführt wird, erfolgt die numerische Auswertung über das ideale Quadrat -1 ≤ ξ ≤ 1, -1 ≤ η ≤ 1,
Die Jacobi ist im Allgemeinen eine rationale Funktion (Polynome sowohl im Zähler als auch im Nenner), so dass sie mit dieser Art der numerischen Quadratur möglicherweise nicht einmal genau integrierbar ist. Aus diesem Grund ist es ratsam, einen gewissen Spielraum bei der gewählten Integrationsreihenfolge zu haben. Der Jacobi-Effekt ist übrigens ein Grund dafür, dass stark verzerrte Elemente schlechter abschneiden als solche mit einer idealen Form. Dieser Blog-Beitrag über die Inspektion eines Netzes in COMSOL Multiphysics enthält weitere Informationen zur Netzqualität.
Auch wenn eine Elementformfunktion als “quadratisch” bezeichnet wird, kann sie (in einigen Fällen) Terme höherer Ordnung enthalten. Die in der Benutzeroberfläche angezeigte Reihenfolge der Formfunktionen zeigt das höchste vollständige Polynom innerhalb der Formfunktionen an. Die Tatsache, dass in den Polynomen einige Terme höherer Ordnung enthalten sein können, ist ein weiterer Grund, eine genauere Integrationsregel zu verwenden, als es auf den ersten Blick notwendig erscheint.
Ein weiterer Grund dafür, dass Sie im Equation View für einen bestimmten Beitrag eine höhere Integrationsordnung sehen als erwartet, ist, dass es notwendig sein kann, die Symmetrie in einer Steifigkeitsmatrix sicherzustellen.
Modifikation der Integrationsordnung
Sie können die Integrationsreihenfolge für jeden schwachen Ausdruck im Equation View ändern, indem Sie das Textfeld bearbeiten. Es gibt zwei Hauptgründe, warum Sie das tun sollten.
Der erste ist der offensichtlichere: Sie möchten die Genauigkeit verbessern. Nehmen wir an, Sie haben eine Last (im allgemeinen Sinne; das kann eine Kraft, ein Wärmestrom, ein elektrischer Strom usw. sein), die im Vergleich zur Elementgröße schnell variiert. Wenn Sie die Ordnung der numerischen Integration erhöhen, wird die Genauigkeit der Gesamtkraft oder des Flusses in das Gebiet verbessert. Die lokale Lösung in der Nähe der Randbedingung wird jedoch immer noch nicht gut sein, da sie nie besser sein kann als das, was die Formfunktionen des Elements darstellen können.
Es gibt jedoch einen weiteren interessanten Fall: Reduzierte Integration, was bedeutet, dass die Integrationsreihenfolge aus irgendeinem Grund niedriger ist, als es formal erforderlich wäre. Ein solcher Grund ist die Beschleunigung der Berechnungen. Bei der Lösung eines Finite-Elemente-Problems wird der größte Teil der CPU-Zeit für zwei Aufgaben verwendet: Die Bildung von Elementmatrizen (Aufbau) und die Lösung großer Systeme linearer Gleichungen. Die Zeit, die für die Lösung der Gleichungen aufgewendet wird, steigt schneller als die Größe des Modells, oft ungefähr mit dem Quadrat der Anzahl der Elemente. Der Zeitaufwand für den Aufbau ist direkt proportional zur Modellgröße (eigentlich zur Anzahl der Elemente multipliziert mit der Anzahl der Integrationspunkte pro Element). Bei einem sehr großen Modell wird die Lösung der Gleichung immer dominieren, aber bei mittelgroßen nichtlinearen Modellen mit umfangreichen Berechnungen in jedem Integrationspunkt kann es sich lohnen, die reduzierte Integration in Betracht zu ziehen.
Die reduzierte Integration ist auch ein numerisches Hilfsmittel, das manchmal verwendet wird, um künstliche Steifigkeit zu entfernen, die in einigen Elementformulierungen in einem Phänomen auftauchen kann, das oft als Locking bezeichnet wird. Ein Beispiel, bei dem die reduzierte Integration zu diesem Zweck eingesetzt wird, findet sich bei dem Interface Shell in der 2D-Achsensymmetrie. In den Gleichungen der virtuellen Arbeit werden einige Terme mit der Ordnung 2 und andere mit der Ordnung 4 integriert. Würde man überall die volle Integration verwenden, würde das Element tatsächlich viel zu steif werden, wenn die Schalendicke klein wird. Durch die Verwendung der reduzierten Integration gehen einige problematische Terme in der Dehnungsenergie absichtlich verloren.

Beiträge der virtuellen Arbeit für das achsensymmetrische Shell Interface.
Hinweis des Herausgebers: Der folgende Abschnitt wurde am 4. Mai 2023 hinzugefügt, um Informationen über neue Funktionen zu ergänzen, die ab Version 6.0 von COMSOL Multiphysics verfügbar sind.
Integrierte reduzierte Integration
Einige der Structural Mechanics-Interfaces bieten die Option, die reduzierte Integration direkt aus den Einstellungen eines bestimmten Materialmodells auszuwählen.
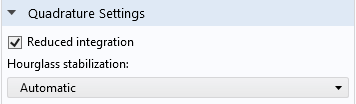
Der Abschnitt Quadrature Settings im Einstellungsfenster für Linear Elastic Material.
Dieser Ansatz hat mehrere Vorteile gegenüber der Bearbeitung der Integrationsreihenfolge im Equation View:
- Die Änderung kann an einer Stelle vorgenommen werden und wird automatisch auf alle möglichen Unterknoten übertragen.
- Sie müssen sich keine Gedanken über das geeignete reduzierte Integrationsschema machen.
- Für einige Elementformfunktionen wird die Steifigkeitsmatrix singulär, wenn die Integrationsordnung reduziert wird. Dies wird durch das integrierte Feature Hourglass stabilization vermittelt.
- Einige Materialmodelle, wie Plastizität, enthalten lokale Zustände in Integrationspunkten. Dies wird automatisch mit der Integrationsregel synchronisiert.
Integrations-Kopplungsoperatoren
Unter Definitions im Model Builder können Sie Integrationsoperatoren erstellen. Solche Operatoren können verwendet werden, um globale Variablen zu definieren, die Teil Ihrer Problemformulierung sind, aber sie können auch explizit in Ausdrücken während der Ergebnisauswertung verwendet werden.
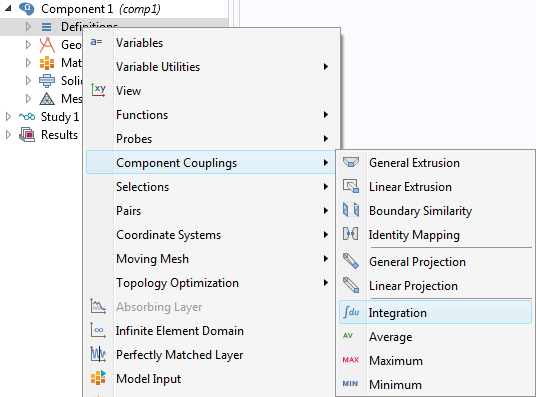 Hinzufügen eines Integrationsoperators.
Hinzufügen eines Integrationsoperators.
Wenn Sie einen Integrationsoperator hinzufügen, müssen Sie im Wesentlichen drei Auswahlen treffen:
- Die Gebiete, Ränder oder Kanten, über die das Integral gebildet werden soll.
- Die Integrationsreihenfolge – Damit haben Sie auch die Möglichkeit, Genauigkeit gegen Geschwindigkeit einzutauschen. Beachten Sie, dass der eigentliche Integrand nicht nur der von Ihnen gelieferte Ausdruck ist, sondern dass er auch mit dem Jacobi der Transformation von der idealen zur realen Elementform multipliziert wird.
- Der Rahmen – Dies wird nur dann wichtig, wenn verschiedene Rahmen existieren, wie z.B. bei bewegten Netzen, verformter Geometrie und geometrischer Nichtlinearität in der Strukturmechanik. Einfach ausgedrückt: Soll das Integral über eine verformte oder unverformte Geometrie gebildet werden?
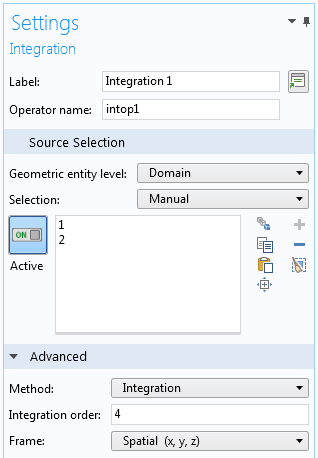
Einstellungen für einen Integrationsoperator.
Integration während des Postprocessings
Wenn Sie beim Postprocessing ein Integral berechnen möchten, haben Sie zwei Möglichkeiten: Sie können einen Integrationsoperator verwenden (wie oben beschrieben) oder einen Integration-Knoten unter Derived Values hinzufügen. Die Wahl ist weitgehend willkürlich. Allerdings können Sie im Knoten Integration den Rahmen für die Integration nicht explizit auswählen. Er wird aus der Rahmenauswahl im Knoten Data Set abgeleitet.
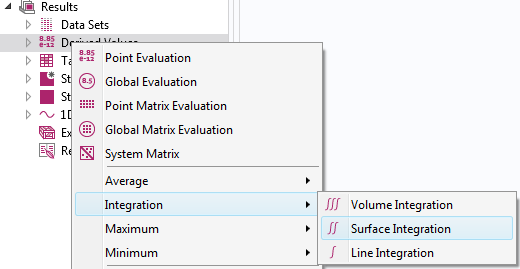
Hinzufügen eines Knotens für die Integration während der Ergebnisbewertung.
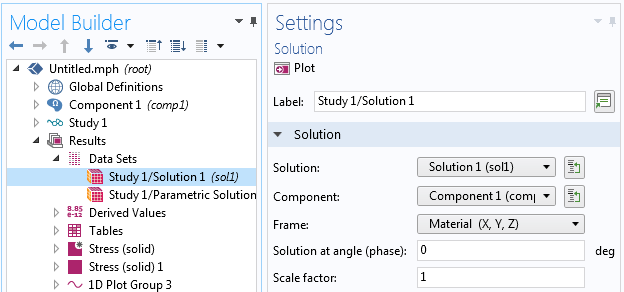
Einstellungen für einen Datensatz, in dem der Rahmen für die Ergebnisinterpretation ausgewählt werden kann.
Wenn die Auswahl des Rahmens wichtig ist, sollten Sie sich wahrscheinlich auf Integrationsoperatoren verlassen, um das Risiko von subtilen Fehlern zu minimieren. Wenn Sie einen Integrationsoperator hinzufügen, nachdem Sie das Problem gelöst haben, müssen Sie Update Solution ausführen, bevor der neue Operator zugänglich ist.
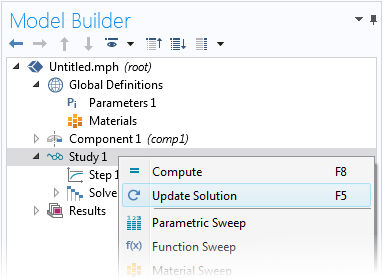
Aktualisieren einer Lösung.
Denken Sie daran, eine ausreichend hohe Integrationsordnung zu wählen. Seien Sie vor allem dann vorsichtig, wenn die zu integrierenden Ausdrücke stark nichtlinear oder diskontinuierlich sind. Ein häufiger Spezialfall von unstetigen Ausdrücken sind Boolesche Ausdrücke. Wenn Sie zum Beispiel nach einer Analyse des Wärmetransports das Volumen berechnen möchten, in dem die Temperatur über einem bestimmten Wert liegt, können Sie einen Integranden wie T>1066[K] verwenden. Dieser Ausdruck ergibt dort, wo die Bedingung erfüllt ist, den Wert 1 und andernorts den Wert 0. Wenn Sie ihn also integrieren, erhalten Sie das Volumen, in dem die Bedingung erfüllt ist. Allerdings wird die Grenze zwischen den beiden Werten im Allgemeinen Elemente durchschneiden.
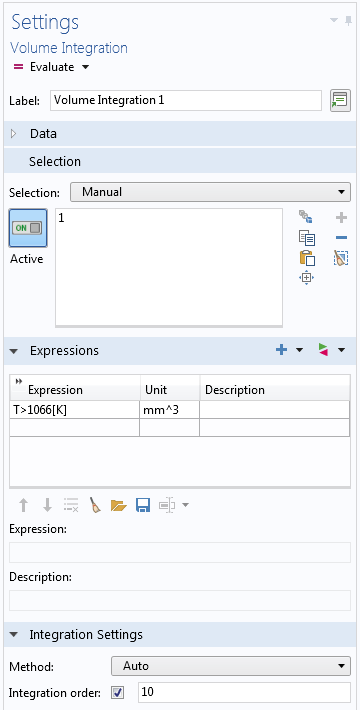
Integration eines Booleschen Ausdrucks mit erhöhter Integrationsgenauigkeit.
Gauß-Punkt-Formfunktionen
Wenn Sie Erweiterungen an Ihrem Multiphysik-Modell vornehmen, müssen Sie manchmal benutzerdefinierte Freiheitsgrade (abhängige Variablen) hinzufügen. Dabei müssen Sie den Typ der Formfunktion auswählen, mit der sie dargestellt werden sollen. Eine der Optionen ist Gauß Point Data. Alle anderen Optionen liefern verschiedene Arten von Feldern, die eine kontinuierliche Verteilung über das Element haben und zwischen benachbarten Elementen kontinuierlich sein können oder auch nicht. Der Typ Gauß Point Data der “Formfunktion” ist grundlegend anders. Er speichert nur einen Wert an jedem Gauß-Punkt, hat aber keine Verbindung zu Werten an anderen Stellen des Elements.
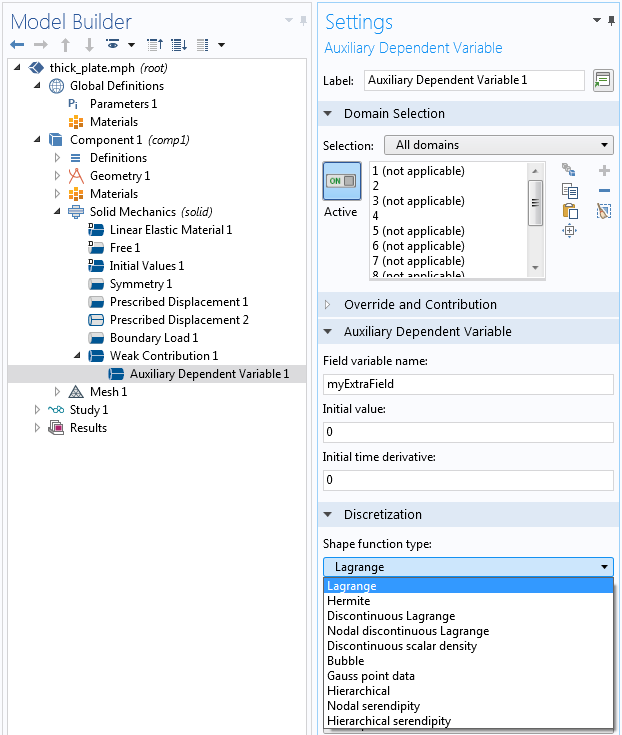
Auswahl des Formfunktiontyps für eine benutzerdefinierte Variable.
Der Typ Gauß Point Data ist nützlich, wenn Sie einen lokalen Zustand speichern möchten. Diese Situation tritt zum Beispiel bei geschichtsabhängigen nichtlinearen konstitutiven Modellen auf, die einen “Speicher” benötigen. Auf das konstitutive Modell wird hauptsächlich bei der Berechnung von Steifigkeitsmatrizen und Residuen zugegriffen, so dass die einzigen Stellen im Element, an denen es während der Lösung tatsächlich ausgewertet wird, an den Integrationspunkten liegen. Daher ist es sinnvoll, diese Art von Daten auch genau dort zu speichern.
Ein Beispiel für die interne Verwendung von Gauß-Punkt-Daten ist die Speicherung inelastischer Dehnungen in Materialmodellen, wie z.B. Plastizität und Kriechen in der Strukturmechanik.
Sobald Sie sich für die Speicherung von Gauß-Punkt-Daten entschieden haben, müssen Sie die Elementordnung auswählen. Im Falle von Gauß-Punkt-Daten ist dies die gleiche wie die oben beschriebene Integrationsreihenfolge. Die Kosten (in Form von Speicherplatz und CPU-Zeit) für das Speichern von Gauß-Punkt-Daten sind proportional zur gewählten Ordnung in 1D, ihrem Quadrat in 2D und der dritten Potenz in 3D.
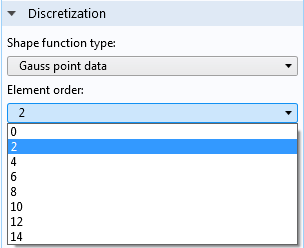
Auswahl des Integrationspunktmusters.
Wenn Sie Gauß-Punkt-Variablen hinzufügen, die zusammen mit einem eingebauten Physik-Interface verwendet werden sollen, sollten Sie in der Regel die gleiche Integrationsreihenfolge wählen wie die, die für die Berechnung der entsprechenden schwachen Ausdrücke verwendet wird. Wenn die Reihenfolge nicht übereinstimmt, müssen die Werte zwischen verschiedenen Stellen im Element übertragen werden, was zu einem Verlust an Genauigkeit und Leistung führt.
Der Operator gpeval
Wenn Sie Variablen in Gauß-Punkten gespeichert haben, die entweder integriert oder von Ihnen definiert wurden, gibt es Situationen, in denen Sie sie über das Element interpolieren müssen. Dies ist besonders bei der Nachbearbeitung wichtig. Standardmäßig werden die Werte von Gauß-Punkt-Variablen einfach vom nächstgelegenen Gauß-Punkt genommen, wenn sie an einer anderen Stelle im Element ausgewertet werden. Der Operator gpeval() kann verwendet werden, um die diskreten Gauß-Punkt-Daten auf ein kontinuierliches Feld abzubilden. In seiner einfachsten Form wird der Operator als gpeval(gporder, expression) referenziert, zum Beispiel gpeval(4,solid.epe). Weitere Einzelheiten entnehmen Sie bitte dem COMSOL Multiphysics User’s Guide.
Zur Veranschaulichung betrachten Sie das folgende Beispiel: Die x-Koordinate (im Bereich von 0 bis 3) wird als Gauß-Punkt-Daten in einem kleinen Drei-Elemente-Modell gespeichert. Dazu fügen Sie eine abhängige Hilfsvariable hinzu, wie unten gezeigt.
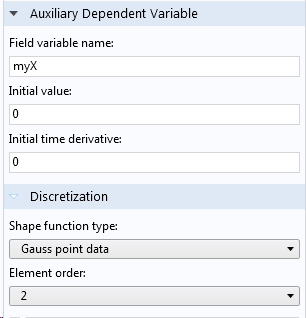
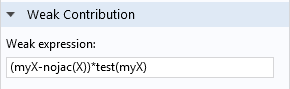
Speichern der x-Koordinate als Gauß-Punkt-Daten.
Der schwache Beitrag (myX-nojac(X))*test(myX) besagt lediglich: “Setzen Sie die Variable myX gleich dem aktuellen Wert von X.” Der Operator nojac() wurde hinzugefügt, um eine bidirektionale Kopplung zwischen myX und X zu verhindern. Sie sollten ihn verwenden, wenn Sie nur einer abhängigen Variablen einen Wert zuweisen wollen.
Wenn die Gauß-Punkt-Variable myX dann als Oberflächendiagramm gezeichnet wird (ohne Mittelwertbildung zwischen den Elementen), ist das Ergebnis diskontinuierlich. Innerhalb jedes Elements werden die Gauß-Punkt-Variablen an die nächstgelegene Ecke verschoben und dann über das Element interpoliert. Wenn stattdessen der Ausdruck gpeval(2,myX) dargestellt wird, erhalten wir die genaue x-Koordinatenverteilung.
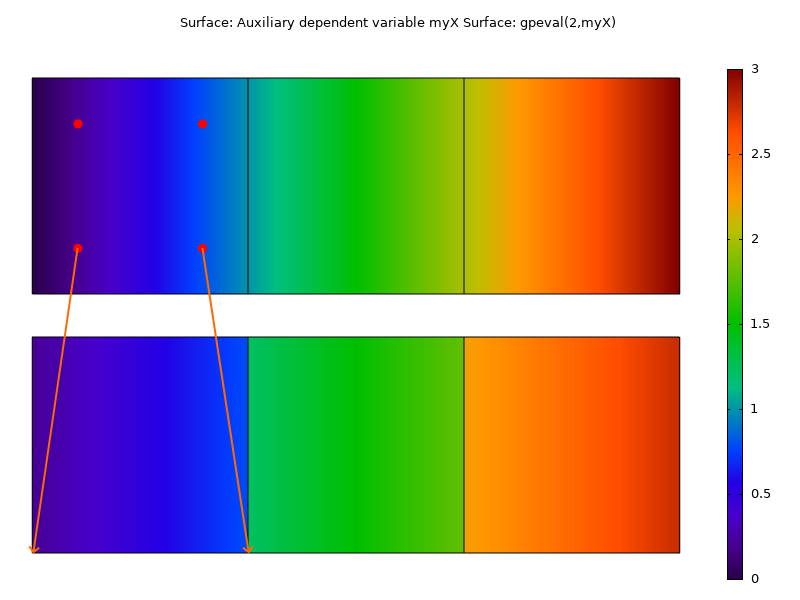
Darstellung der Gauß-Punkt-Variablen (unten) und der extrapolierten Gauß-Punkt-Variablen (oben). Die Pfeile zeigen an, wie die Gauß-Punkt-Daten bei der Ergebnisauswertung entsprechend der Standardeinstellung in die Ecken verschoben werden.
Nächste Schritte
Erfahren Sie mehr über die in der COMSOL® Software verfügbaren Funktionen, indem Sie auf die Schaltfläche unten klicken:




Kommentare (0)