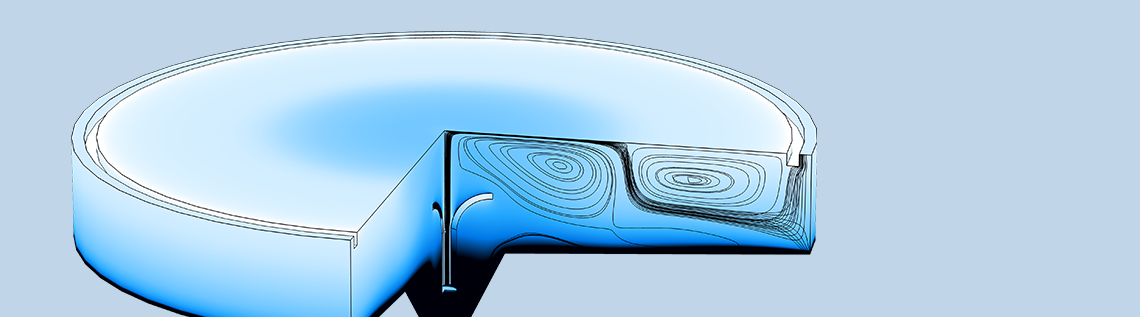
Das Festlegen von Randbedingungen für den Ein- und Auslass in einer CFD-Simulation

Bei der Erstellung von Strömungssimulationen konzentrieren wir uns in der Regel auf einzelne (möglicherweise einige) Komponenten in einem größeren System, z. B. eine Pumpe oder ein Absetzbecken in einer Wasseraufbereitungsanlage. Dies wirft natürlich eine Frage auf: In welchem Abstand können wir Randbedingungen anwenden, ohne dass sie sich auf die Strömung auswirken? In diesem Blog-Beitrag befassen wir uns mit den Auswirkungen der Nähe von Ein- und Auslässen für innere und äußere Strömungen einer homogenen Flüssigkeit mit vernachlässigbarer Kompressibilität.

Setzen von Ein- und Auslassrandbedingungen für innere Strömungen

CFD-Simulationen sind in der Regel sehr rechenintensiv, und wir versuchen daher, die Freiheitsgrade in unseren Simulationen zu minimieren. Wenn wir es auf die Spitze treiben, könnten wir mit einer Geometrie enden, in der sich ein Einlass- und ein Auslassrand überschneiden. Betrachten wir eine scharfe 90°-Biegung in einem Rohr mit halbkreisförmigem Querschnitt.

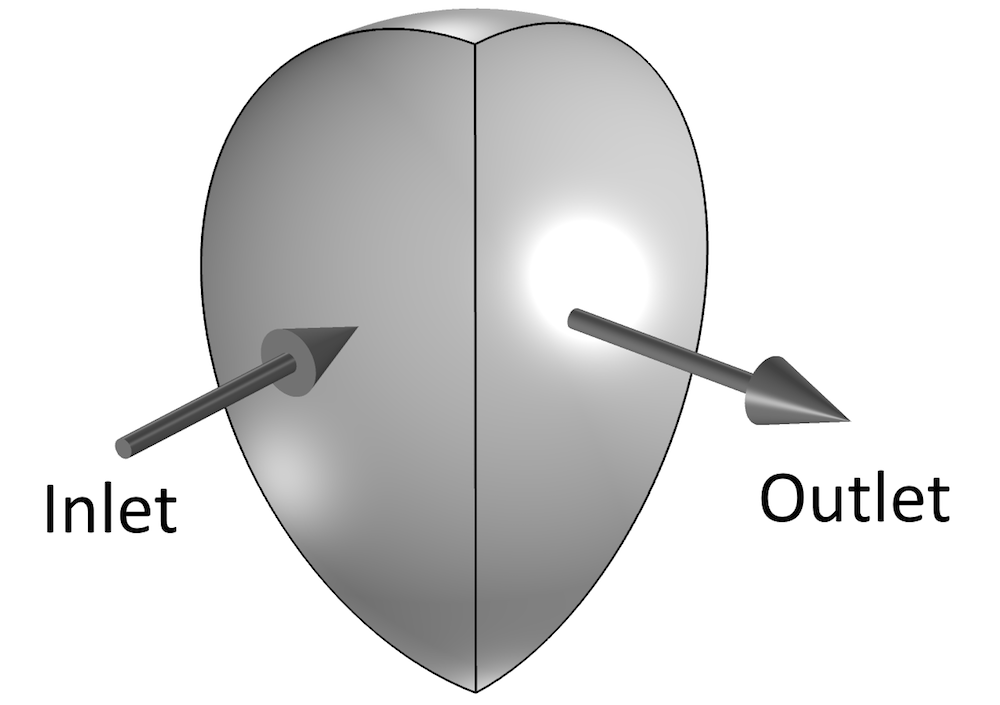
Ein Rohr mit einer 90°-Biegung und einem halbkreisförmigem Querschnitt.

Wenn die Simulation mit der oben gezeigten Geometrie durchgeführt wird, haben die Einlass- und Auslassränder eine gemeinsame Kante. In vielen Fällen kann allein dieser Umstand zu ernsthaften Konvergenzproblemen führen. In diesem speziellen Fall konvergiert die Lösung jedoch innerhalb weniger Iterationen. Wir betrachten auch eine entsprechend eingerichtete Simulation mit Einlass- und Auslassrohren, die auf eine Länge von 10 Radien erweitert wurden (siehe unten).

Eine 90°-Biegung mit verlängerten Einlass- und Auslassrohren.

Die Simulationen werden für eine Reynolds-Zahl von 120 auf der Grundlage des hydraulischen Durchmessers D_{h}=4A/P durchgeführt, wobei A die Fläche des Querschnitts und P sein Umfang ist. An den Einlässen wird ein gleichmäßiges Geschwindigkeitsprofil und an den Auslässen eine Normalspannung von Null angelegt. Die folgende Abbildung zeigt den Druck an der Biegung für die beiden Simulationen mit verlängerten Einlass- und Auslassrohren auf der linken Seite und ohne diese Rohre auf der rechten Seite. Für den Fall mit verlängerten Einlass- und Auslassrohren wird der mittlere Druck an dem stromabwärts gelegenen Rand vom Absolutwert abgezogen, so dass beide Ergebnisse an diesem Rand einen mittleren Druck von Null ergeben.

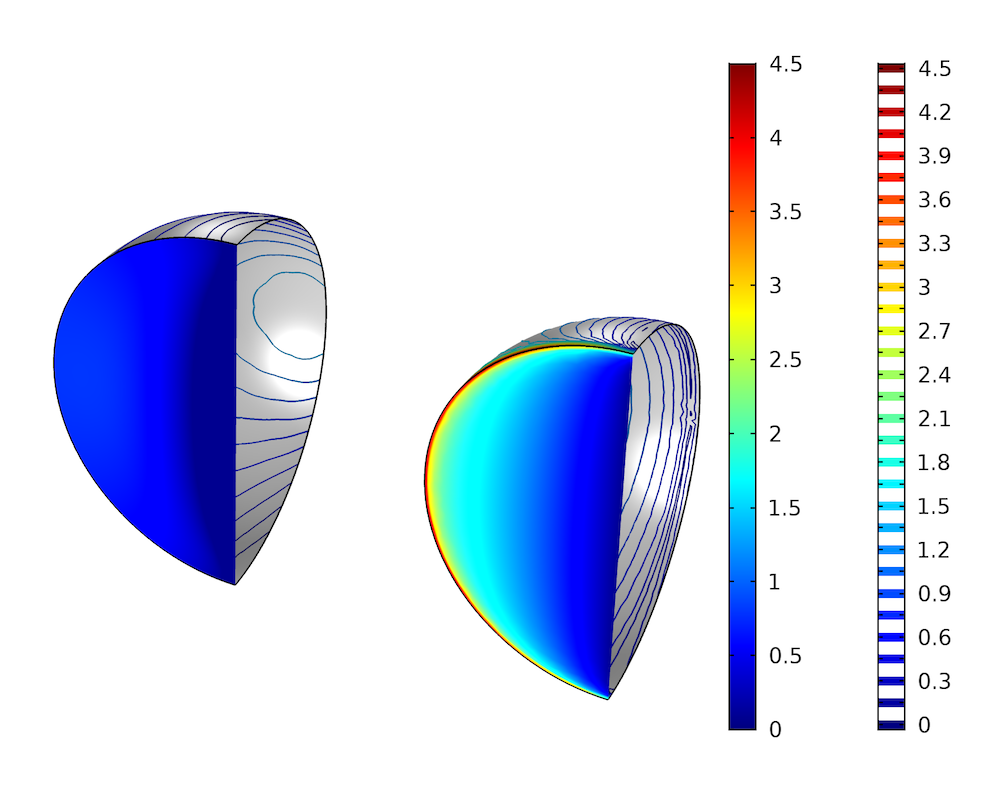
Druckschwankungen an einer 90°-Biegung in einem Rohr mit halbkreisförmigem Querschnitt, mit Oberflächendarstellung des Drucks an dem stromaufwärts gelegenen Rand und Druckkonturen an den Rohrwänden. Das linke Diagramm zeigt die Ergebnisse mit verlängerten Einlass- und Auslassrohren und das rechte Diagramm die Ergebnisse ohne diese Rohre.

Die Ergebnisse der Simulation ohne verlängerte Einlass- und Auslassrohre zeigen eine viel größere Druckschwankung. Es gibt ein starkes Druckgefälle an der Wand neben dem Einlass, was auf die Inkompatibilität zwischen dem angewandten gleichmäßigen Geschwindigkeitsprofil und der No Slip-Randbedingung an der Wand zurückzuführen ist. Das Diagramm auf der linken Seite zeigt einen viel gleichmäßigeren Druck auf der stromaufwärts gelegenen Seite der Kurve, was darauf hindeutet, dass die Strömung voll entwickelt ist, wenn sie die Kurve erreicht. Der Druck ist jedoch nicht völlig gleichmäßig: In der Nähe der scharfen Ecke ist er etwas niedriger. Dies deutet auf einen stromaufwärts gerichteten Einfluss der Kurve hin. Wir sehen auch einen Stagnationspunkt an der Rohrwand gegenüber des stromaufwärts gelegenen Rands. Der Verlustkoeffizient über die Biegung, definiert als

(1)

beträgt 2,3 ohne die Einlass- und Auslassrohre und 0,60 mit ihnen. Weitere Erkenntnisse lassen sich durch einen Blick auf das Geschwindigkeitsfeld gewinnen.

Geschwindigkeitsprofile und Stromlinien in einer 90°-Biegung für ein Rohr mit halbkreisförmigem Querschnitt.

Die obige Abbildung zeigt das Geschwindigkeitsprofil an vier Positionen stromaufwärts und vier Positionen stromabwärts der Biegung sowie die Stromlinien in der Mittelebene. Stromaufwärts ist zu erkennen, wie sich das gleichförmige Geschwindigkeitsprofil in das voll entwickelte Profil verwandelt. An der Biegung sieht man den Stagnationspunkt an der Rohrwand gegenüber dem Einlassrohr und die damit verbundene Rezirkulationszone. Stromabwärts der scharfen Biegung gibt es eine weitere Rezirkulationszone, und wir können sehen, dass das voll entwickelte Profil erst am Ende des Auslassrohrs erreicht wird. All dies ist in der einfachen Geometrie (die nur die 90°-Biegung enthält) nicht enthalten, und es ist nicht überraschend, dass wir einen inkorrekten Druckabfall erhalten.

Die Option Fully developed flow in den Inlet und Outlet Randbedingungen kann verwendet werden, um übermäßig lange Einlass- und Auslassrohre zu vermeiden. Die Ergebnisse in den beiden vorangegangenen Abbildungen deuten stark darauf hin, dass wir diese Bedingungen in einiger Entfernung von der Biegung anwenden sollten, um gute Ergebnisse zu erzielen. Aber wie weit stromaufwärts und stromabwärts müssen wir die Fully developed flow Optionen anwenden? Wenn wir die Einlass- und Auslassrohre um jeweils einen Radius von der Biegung entfernen, ergibt sich ein Verlustkoeffizient von 0,54 für die gesamte Biegung, während zwei Radien in jeder Richtung zu einem Verlustkoeffizienten von 0,58 führen. Von da an ist die Annäherung an den Wert 0,60 langsamer. Daher scheinen zwei Radien in jeder Richtung in diesem Fall ein guter Kompromiss zu sein.

Mit zunehmender Reynoldszahl wird die Rezirkulationszone stromabwärts des Bogens immer länger und schließlich instabil. Bei einer Reynoldszahl von 1200 ändert sich der Verlustkoeffizient nicht nennenswert, wenn das Auslassrohr über 20 Radien hinaus verlängert wird, vorausgesetzt, dass die Option Fully developed flow am Ende des Rohrs angewendet wird. Aus Korrelationen für Eingangslängen in Rohren,

(2)

für laminare Strömung und

(3)

für turbulente Strömung, können wir abschätzen, wie weit stromabwärts der Kurve das voll entwickelte Strömungsprofil erreicht wird. Beachten Sie, dass die Eintrittslänge der turbulenten Strömung in der Regel kürzer ist als die Eintrittslänge der laminaren Strömung mit hoher Reynolds-Zahl. Wir müssen zu Reynolds-Zahlen von O(10^8) übergehen, damit die Eintrittslänge O(10^2) hydraulische Durchmesser erreicht.

Für die beiden laminaren Fälle mit Reynolds-Zahlen von 120 und 1200 betragen die aus (2) ermittelten Eintrittslängen etwa 7,5 bzw. 75 Radien. Bei Verwendung der Option Fully developed flow an den Auslässen erhalten wir gute Ergebnisse mit Auslassrohren, die 1/3 dieser Längen entsprechen.

Der Einfluss stromaufwärts sollte mit steigender Reynolds-Zahl abnehmen, da die elliptische Natur der Navier-Stokes-Gleichung mit steigender Reynolds-Zahl abnimmt. Wir können den Bereich des stromaufwärts gerichteten Einflusses abschätzen, indem wir uns die Potentialströmung in einer ähnlichen Geometrie ansehen.

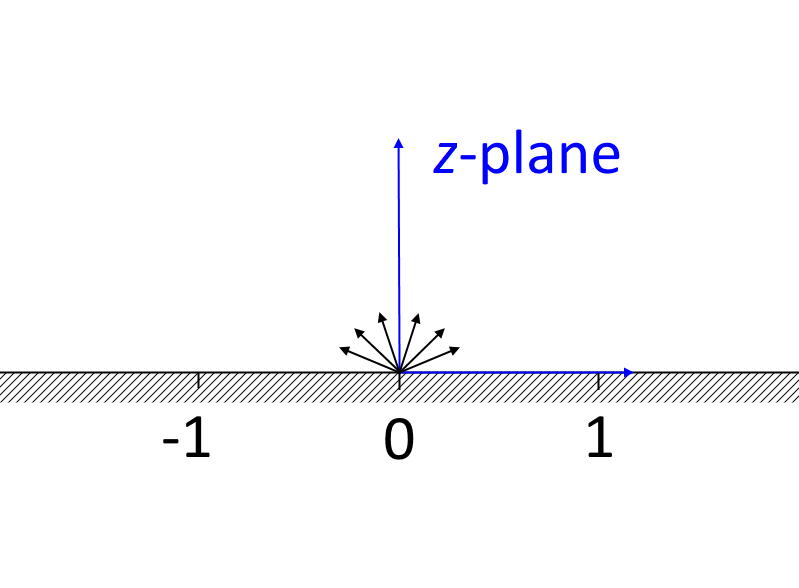
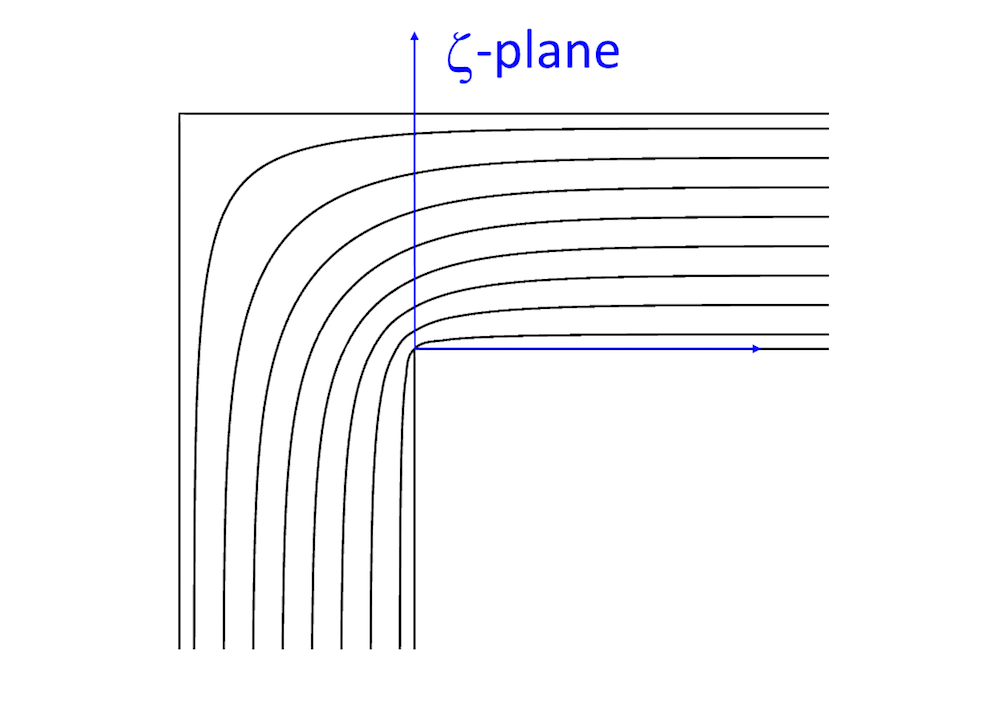
Übertragung der oberen Hälfte der Ebene auf eine scharfe 90°-Biegung mithilfe der Schwarz-Christoffel-Transformation.

Mithilfe der Schwarz-Christoffel-Transformation (Ref. 1) kann die obere Hälfte der Ebene in der komplexen z-Ebene auf eine scharfe 90°-Biegung in der komplexen \zeta-Ebene abgebildet werden. Der Einlass, der sich bei -i\infty in der \zeta-Ebene befindet, entspricht einer Quelle im Ursprung in der z-Ebene, während sich der Auslass in beiden Ebenen bei \infty befindet. Der äußere und der innere Winkel der Biegung in der \zeta-Ebene entsprechen den Punkten -1 bzw. 1 in der z-Ebene. Das Geschwindigkeitsfeld in der \zeta-Ebene erhält man in impliziter Form als

(4)

Die folgende Abbildung zeigt den Druckkoeffizienten entlang der Innenwand als Funktion des dimensionslosen Abstands stromaufwärts der Biegung für die Lösung der Potentialströmung.

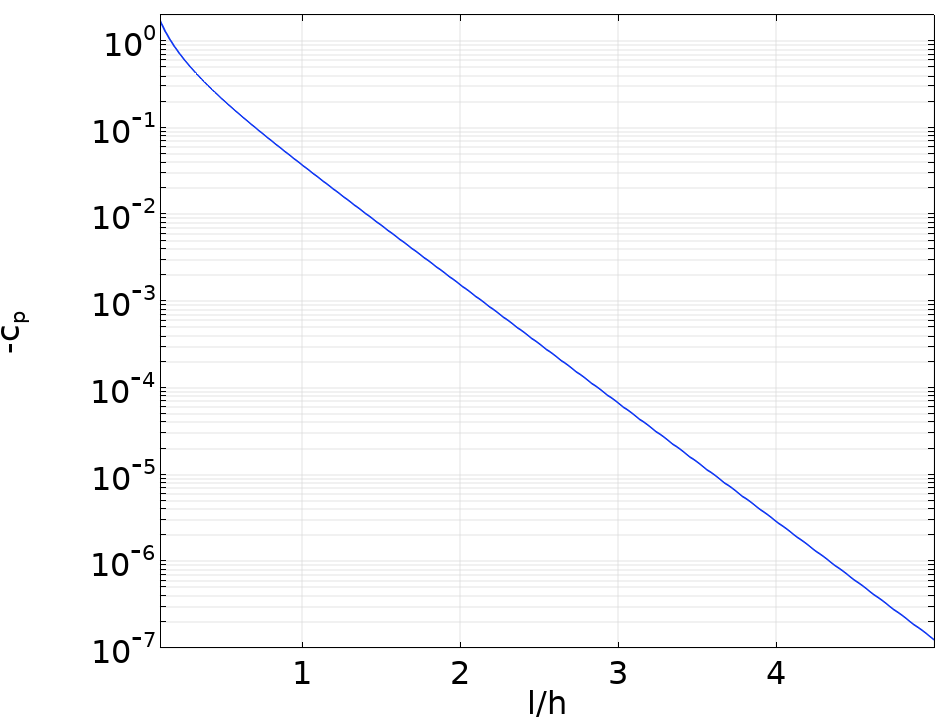
Der Druckkoeffizient entlang der Innenwand vor einer scharfen 90°-Biegung.

In dieser Abbildung basiert der Druckkoeffizient auf der Differenz zwischen dem lokalen Druck und dem Druck weit stromaufwärts, und h ist die Kanalbreite. Wir stellen fest, dass der Druckkoeffizient O(10^{-3}) ist, wenn der stromaufwärts gelegene Abstand zur Biegung zwei Kanalbreiten beträgt. Unter der Voraussetzung, dass wir die Option Fully developed flow am Einlass verwenden, müssen wir also unser Einlassrohr (oder den Kanal) nur um einige hydraulische Durchmesser stromaufwärts verlängern.

Berücksichtigung der Schwerkraft

Die Option Fully developed flow in den Randfunktionen Inlet und Outlet ist mit der zusätzlichen Option Compensate for hydrostatic pressure (inkompressible Strömung) oder Compensate for hydrostatic pressure approximation (schwach kompressible oder kompressible Strömung) ausgestattet, wenn die Schwerkraft im Modell aktiv ist. Diese zusätzliche Option liefert das exakte hydrostatische Druckprofil an dem Rand für inkompressible Strömung und eine gute Annäherung für schwach kompressible Strömung und kompressible Strömung. Besondere Vorsicht ist geboten, wenn das Fluid an den Einlass- oder Auslassrändern stark geschichtet ist, wie z. B. bei mehrphasiger Strömung. In diesen Fällen kann es sinnvoll sein, eine Kammer hinzuzufügen, in der die Strömung parallel zum Schwerkraftvektor verläuft.

Probleme können auch auftreten, wenn gegen die Schwerkraft gearbeitet wird. Die Abbildung unten zeigt ein großes Absetzbecken mit einer langen Verweilzeit, so dass sich die suspendierte (schwere) Phase absetzen und durch den Bodenauslass austreten kann. Die leichte Phase tritt vertikal durch einen ringförmigen Auslass neben dem äußeren Rand aus. Die grauen Stromlinien entsprechen dem Geschwindigkeitsfeld für die leichte Phase, während die schwarzen Stromlinien dem Geschwindigkeitsfeld für die schwere Phase entsprechen. Ein kleiner Teil der schweren Phase tritt durch den Auslass für die leichte Phase aus. Hier fließt die schwere Phase in die der Schwerkraft entgegengesetzten Richtung, wodurch sich neben dem äußeren Rand ein kleiner Wirbel bildet, da ein Teil der Schwebeteilchen wieder nach unten fällt. Dieser kleine Wirbel kann sich negativ auf den Zeitschritt auswirken, was zu einer längeren Gesamtberechnungszeit führt. Abhilfe könnte ein Überlauf (ein Wehr) schaffen, durch den die Strömung in Richtung der Schwerkraft abfließen kann.

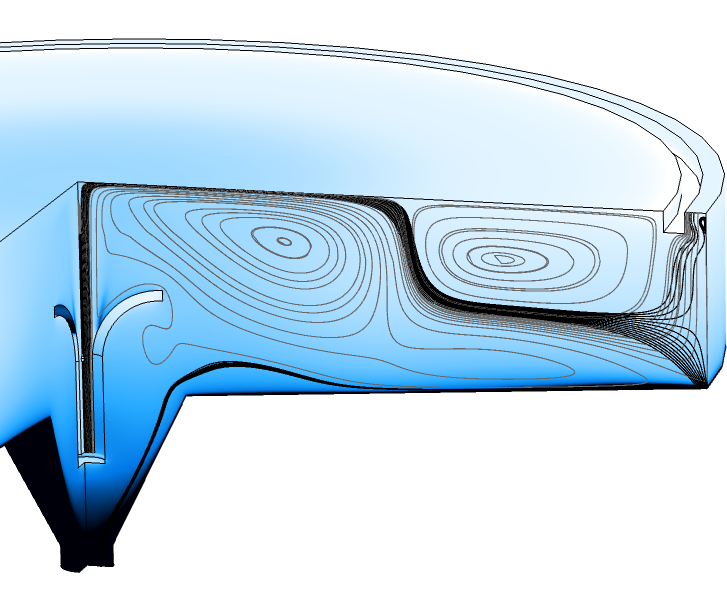
Volumenanteil der gelösten Phase (Farbkarte) und Stromlinien, grau für die leichte Phase und schwarz für die schwere Phase, in einem Absetzbecken.

Ein weiteres Beispiel für einen Fall, in dem sich Einfluss- und Ausflussränder überschneiden, tritt bei der Simulation einer Wärmewolke auf, die unten dargestellt ist. In diesem Fall wird an dem Einlassrand (die zylindrische Fläche in der Abbildung) keine Inlet Randbedingung vorgeschrieben. Stattdessen wird die Funktion Open Boundary angewendet. Sowohl im Open BoundaryFeature als auch im OutletFeature (oberer Rand) wird die Option Compensate for hydrostatic pressure approximation angewendet. Dies ist unerlässlich, da der auftriebsbedingte Druck im Modell um drei Größenordnungen geringer ist als der hydrostatische Druck. Eine weitere wichtige Option ist die Option Suppress backflow in der Funktion Outlet.

Turbulente Wärmewolke mit Darstellung der Geschwindigkeit (Farbschema) und Konturen der Druckabweichungen von den hydrostatischen Bedingungen.

Die kleinen Störungen der Konturlinien am oberen Rand sind auf die Inkonsistenz mit einem konstanten Druck zurückzuführen. Diese können durch die Verwendung der Option Boussinesq Approximation im Multiphysik-Kopplungsknoten Nonisothermal Flow eliminiert werden.

Einlass- und Auslassränder für die äußere Strömung festlegen

Bei Außenströmungsanwendungen, wie z. B. der Umströmung von Fahrzeugen und Gebäuden, werden die Bedingungen in großer Entfernung vom Hindernis in der Regel auf einen konstanten Geschwindigkeitsvektor an den Einlassrändern und einen konstanten Druck an den Auslassrändern festgelegt. Auch hier stellt sich die Frage, inwieweit der Abstand vom Hindernis, in dem diese Bedingungen angewendet werden, die Lösung beeinflusst. Bei der Außenströmung zeigt sich, dass dieser Abstand mit den räumlichen Dimensionen des Modells variiert. Bei 2D-Modellen ist der erforderliche Abstand um eine Größenordnung größer als bei achsensymmetrischen 3D- und 2D-Modellen. Um zu verstehen, warum dies so ist, betrachten wir noch einmal die idealen Lösungen für Potentialströmungen.

Bei der Außenströmung um ein Hindernis entsteht Wirbelstärke in Randschichten auf der Festkörperoberfläche. Die Randschichten auf verschiedenen Seiten des Hindernisses können an der Hinterkante zusammenfließen und eine dünne Wirbelschicht bilden, die stromabwärts in ein Kielwasser fließt. Wenn sich die Randschicht auf einer Seite aufgrund von Instabilität oder einer scharfen konvexen Ecke vom Hindernis trennt, wird das Kielwasser breiter sein. In beiden Fällen bleibt die stromabwärts entweichende Wirbelstärke auf das Kielwasser beschränkt, und die Strömung außerhalb des Kielwassers ist annähernd wirbelfrei.

Turbulente Strömung um eine NACA Tragfläche. Die Randschicht auf der Oberseite des Profils trennt sich vor der Hinterkante.

Das Hindernis und sein Kielwasser verschieben die Stromlinien des freien Stroms, und wir können uns die Strömung in großen Abständen vom Hindernis als die Summe einer gleichmäßigen Strömung und einer Quelle vorstellen.

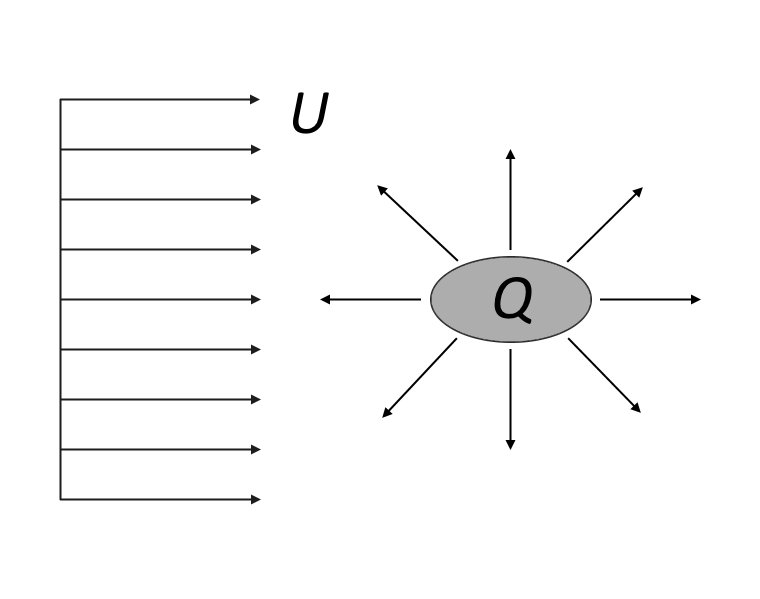
Potentialströmung in großer Entfernung von einem Hindernis und seinem Kielwasser.

Die resultierenden Geschwindigkeitsfelder in 2D und 3D können ausgedrückt werden als

(5)

wobei R=\sqrt{x^{2}+y^{2}}, r=\sqrt{x^2+y^2+z^2}, die Quelle im Ursprung liegt und die freie Strömung in die positive x Richtung gerichtet ist.

Die Stärke der Quelle kann in beiden Fällen mit den Abmessungen des Hindernisses in Beziehung gesetzt werden. An der x-Position der Quelle ist die Verschiebung der Stromlinien y_{0}=Q/(4U) im 2D-Fall und r_{0}=\sqrt{Q/(2\pi U)} im 3D-Fall. Die Grenzwerte weit stromabwärts sind y_{\infty}=Q/(2U) bzw. r_\infty=\sqrt{Q/(\pi U)}. Für die Zwecke der vorliegenden Schätzungen kann entweder 2y_{0} oder 2y_\infty in 2D und 2r_{0} oder 2r_\infty in 3D als repräsentativer Wert für die Größe des Hindernisses verwendet werden. Hier verwenden wir d=Q/(2U) in 2D und d=\sqrt{2Q/(\pi U)} in 3D. Aus der Bernoulli-Gleichung lässt sich der Druckkoeffizient bei großen Abständen abschätzen.

(6)

Setzt man die Geschwindigkeitsfelder der Potentialströmung zusammen mit den Schätzungen für die Quellstärken ein, erhält man

(7)

Daher nimmt der Druckkoeffizient mit d/R in 2D und mit (d/r)^2 in 3D ab. Um den Einfluss der äußeren Randbedingungen auf etwa O(10^{-2}) zu reduzieren, müssten wir die äußeren Ränder des Berechnungsbereichs in einer Entfernung von etwa 100 Hindernisgrößen in 2D und 10 Hindernisgrößen in 3D anordnen.

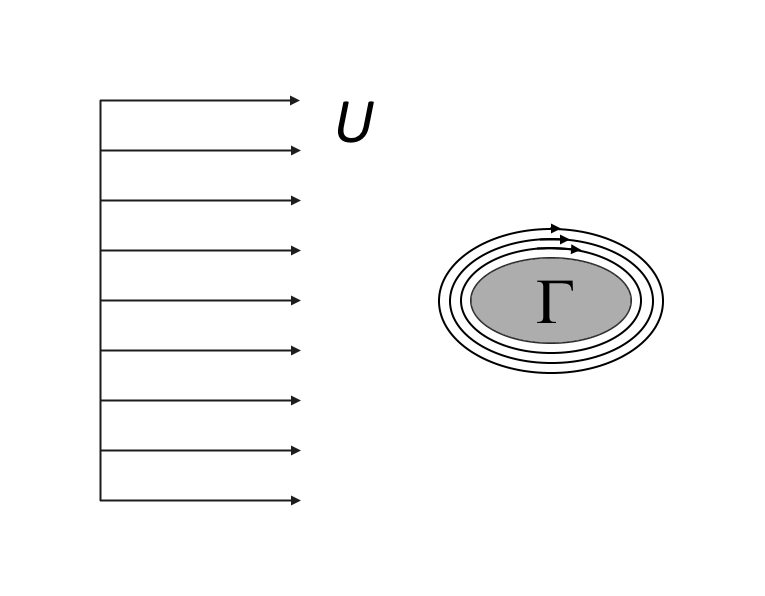
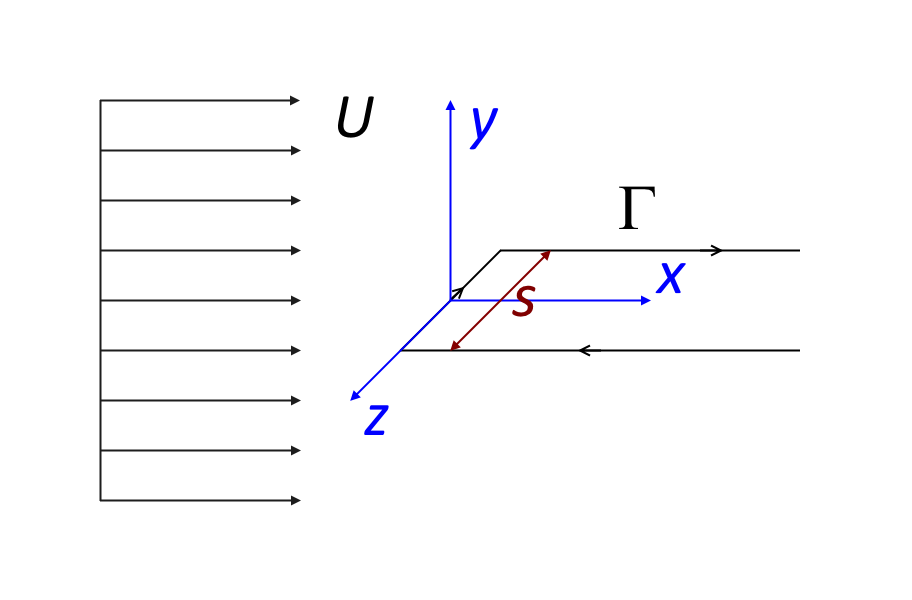
Je nach Form und Ausrichtung des Hindernisses kann die Wirbelablösung eine Zirkulation hervorrufen, die Seitenkräfte (Auftrieb) erzeugt. Die Potentialströmung in großer Entfernung vom Hindernis kann durch eine gleichmäßige Strömung und einen Punktwirbel in 2D oder eine gleichmäßige Strömung und einen hufeisenförmigen Linienwirbel in 3D angenähert werden.

Potentialströmung um ein Hindernis mit Zirkulation (Auftrieb). In 2D (links) besteht die Potentialströmung aus einer gleichmäßigen Strömung in der x-Richtung und einem Punktwirbel im Ursprung. In 3D (rechts) besteht die Potentialströmung aus einer gleichförmigen Strömung in x-Richtung und einem Hufeisenwirbel mit einer Spannweite von s in z-Richtung, der sich in x-Richtung bis ins Unendliche erstreckt.

Bei großen Entfernungen vom Hindernis sind die Geschwindigkeitsfelder der Potentialströmung entsprechend der obigen Abbildung gegeben durch

(8)

Man beachte, dass man die 2D-Lösung aus der 3D-Lösung erhält, indem man z auf Null setzt und s\rightarrow\infty lässt. Die Zirkulation kann in den meisten realisierbaren Fällen mit der Geschwindigkeit der freien Strömung und den Dimensionen des Hindernisses in Stromrichtung (Profiltiefe) c in Beziehung gesetzt werden durch

(9)

wobei \alpha der Angriffswinkel und -\beta der “Null-Auftriebs”-Winkel ist (beide in Radianten).

Letztere ergibt sich aus der Form (Krümmung) des Hindernisses, z. B. der Wölbung einer Tragfläche. Setzt man die asymptotischen Lösungen für die Potentialströmung und den Ausdruck für \Gamma in die Definition des Druckkoeffizienten ein, erhält man

(10)

Der gesamte Ablenkungswinkel, \alpha+\beta, muss mindestens eine Größenordnung kleiner als 1 sein, damit die Schätzung für \Gamma gilt. Für eine Kugel sind die Dimensionen d, c und s gleich. Daher sind die Beschränkungen für die Nähe der äußeren Ränder, die durch die Zirkulation gesetzt werden, weniger streng als die, die durch die Quelle gesetzt werden.

Bei einer Tragfläche sind die drei Dimensionen alle von unterschiedlicher Größenordnung s\sim 10c\sim 100d. In 2D sind die Einschränkungen durch den Punktwirbel genauso groß wie die durch die Quelle, da d\sim c(\alpha+\beta). Würde eine 3D-Tragfläche allein modelliert, wären die Einschränkungen durch den Linienwirbel um den Faktor 100 größer als die durch die Quelle verursachten. Häufig ist das Profil an einem Rumpf mit d\sim c befestigt, so dass beide Einschränkungen im 3D-Fall gleich groß sind. Die folgende Abbildung zeigt eine 2D-Simulation der Umströmung einer NACA 0012-Tragfläche bei einem Angriffswinkel von 14°. Um den Einfluss der äußeren Randbedingungen zu minimieren, wird das Gebiet um 100 Profiltiefen in jede Richtung erweitert. Die relevante Längenskala ist in diesem Fall c\alpha, da \beta=0 für ein symmetrisches Profil. Nach den obigen Schätzungen ergeben sich daraus Druckkoeffizienten von einigen Zehntelprozenten.

2D-Simulation einer NACA 0012-Tragfläche mit einem Angriffswinkel von 14°.

Die folgende Abbildung zeigt eine 3D-Simulation eines Flugzeugs, das einen Strömungsabriss erfährt, mit einem Anstellwinkel von 20°. Der Berechnungsbereich wird durch eine Halbkugel mit einem Radius von 15 m und einen Zylinder mit einer Höhe von 30 m begrenzt. Die Spannweite der Tragfläche beträgt etwa 18 m, der Durchmesser des Rumpfes 2,4 m und die maximale Profiltiefe mal Anstellwinkel etwa 1,3 m. Wenn man diese Zahlen einsetzt, erhält man Druckkoeffizienten von einigen Prozent, was etwas hoch ist. Daher würden sich die Ergebnisse dieser Simulation wahrscheinlich verbessern, wenn der Bereich weiter vom Flugzeug entfernt wäre.

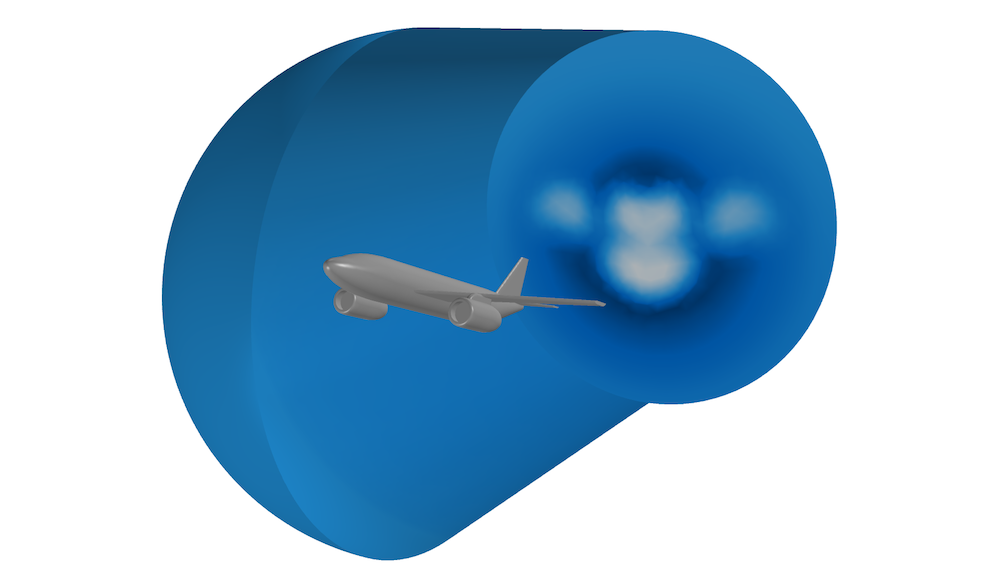
Berechnungsbereich, eingefärbt nach Geschwindigkeitsgröße, für die Simulation eines Flugzeugs, das einen Strömungsabriss erfährt.

Abschließende Gedanken zur Positionierung von Einlass- und Auslass-Randbedingungen

In diesem Blog-Beitrag haben wir die Verwendung der Theorie der idealen Strömung und empirischer Korrelationen zur Bestimmung geeigneter Orte für die Einlass- und Auslassränder demonstriert. Für die innere Strömung haben wir empirische Korrelationen für laminare und turbulente Strömung verwendet, um die für eine voll entwickelte Strömung erforderliche Rohrlänge zu bestimmen. Die entsprechende Ausdehnung des Bereichs stromaufwärts und stromabwärts führte eindeutig zu korrekten Strömungssimulationen. Diese Länge nimmt jedoch mit der Reynolds-Zahl zu und kann, insbesondere bei laminaren Strömungen mit hoher Reynolds-Zahl, zu groß werden. Die Verwendung der Option Fully developed flow in den Rand-Features Inlet und Outlet reduziert diese Länge erheblich. Auf der stromabwärts gelegenen Seite scheint eine Reduzierung der Länge um den Faktor drei ein angemessener Kompromiss zwischen Genauigkeit und Rechenkosten zu sein. Die Anwendung der Potentialströmungstheorie zeigt, dass die stromaufwärts gelegene Strecke nicht länger als ein paar hydraulische Durchmesser sein muss. Bei der Option Fully developed flow wird auch die Schwerkraft berücksichtigt, wenn sie aktiv ist. Probleme können immer noch auftreten, wenn die Strömung stark geschichtet ist, wie z.B. bei mehrphasiger Strömung. In solchen Fällen ist es ratsam, den Auslass in Richtung der Schwerkraft umzuleiten.

Für die Außenströmung wurde die Potentialströmungstheorie verwendet, um die Entfernung abzuschätzen, bei der die durch die Strömung um ein Hindernis verursachten Druckschwankungen vernachlässigbar werden. Es wurde festgestellt, dass der Druck in 2D gemäß \sim D/R und in 3D und 2D Achsensymmetrie gemäß \sim A/R^2 variiert, wobei R der Abstand zum Zentrum des Hindernisses ist, während D und A die Länge bzw. die Fläche des Hindernisses sind, die auf eine Ebene orthogonal zur freien Strömung projiziert werden.

Wir hoffen, dass Ihnen diese Abschätzungen beim Aufsetzen Ihrer eigenen Simulationen nützlich sein werden. Denken Sie jedoch daran, Ihre Ergebnisse zu überprüfen. Wenn Sie die Option Fully developed flow für die innere Strömung verwenden, ist es am einfachsten, die Einlass- und Auslasskanal- oder -rohrlänge zu variieren, um zu sehen, ob sich die Ergebnisse ändern. Bei der Außenströmung sollten Sie überprüfen, ob die Geschwindigkeit nicht mehr als die zulässige Toleranz vom Geschwindigkeitsfeld der freien Strömung an den Druckgrenzen abweicht (außer im Kielwasser). Das Gleiche gilt für den Druck an den Geschwindigkeitsgrenzen.

Referenz

1. R.V. Churchill & J.W. Brown, Complex Variables and Applications, 5^th ed., McGraw-Hill, 1990.

Anmerkung des Herausgebers: Dieser Blog-Beitrag wurde am 25.4.2023 aktualisiert, um zu verdeutlichen, dass die Option Fully developed flow Teil des Plattformprodukts COMSOL Multiphysics^® ist.