In einem vorherigen Blog-Beitrag haben wir verschiedene physikalische Phänomene vorgestellt, die Dämpfung in Strukturen verursachen, und gezeigt, wie diese Dämpfung mathematisch dargestellt werden kann. Heute schauen wir uns an, wie man Dämpfung in Finite-Elemente-Modelle einbezieht.
Berücksichtigung der Dämpfung in der Finite-Elemente-Analyse
Bei der Durchführung einer strukturdynamischen Analyse kann die Modellierung der Dämpfung ein wichtiger und schwieriger Teil der Aufgabe sein.
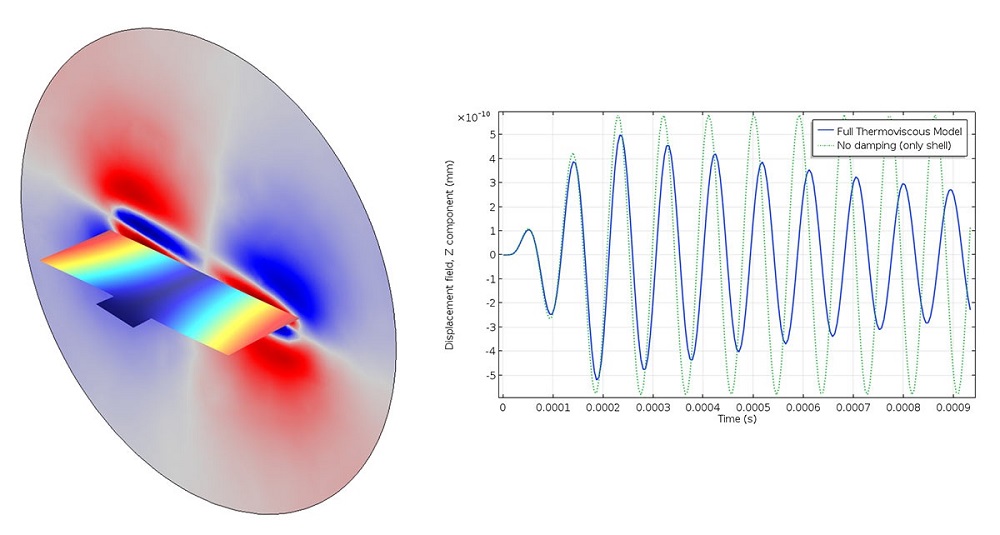
Eine transiente Analyse eines vibroakustischen Mikrospiegels unter Berücksichtigung der viskosen und thermischen Dämpfung.
Im Folgenden finden Sie einen Überblick darüber, was Sie bei der Modellierung von Dämpfungseffekten in Ihren Finite-Elemente-Analysen mit der COMSOL Multiphysics® Software berücksichtigen sollten.
Eigenfrequenzanalyse
Ein Eigenfrequenzproblem kann in COMSOL Multiphysics® mit oder ohne Dämpfung gelöst werden. Sofern es in Ihrem Modell dissipative Effekte gibt, werden diese berücksichtigt und die berechneten Eigenfrequenzen sind komplexwertig. Dies geschieht automatisch, so dass Sie keine besonderen Einstellungen im Löser vornehmen müssen.
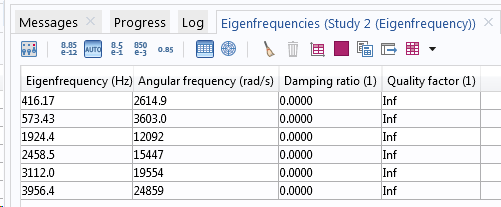
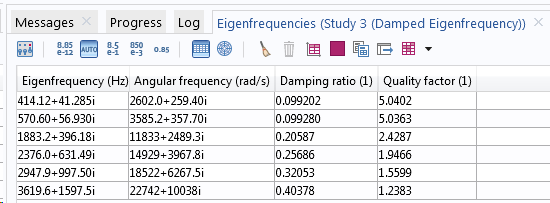
Eigenfrequenzen in einem Modell ohne (obere Tabelle) und mit Dämpfung (untere Tabelle).
In den meisten Fällen, in denen Dämpfung auftritt, sind nicht nur die Eigenfrequenzen, sondern auch die Eigenmoden komplexwertig. Die Interpretation einer komplexwertigen Modenform besteht darin, dass der Phasenwinkel Informationen über die Phasenverschiebung zwischen verschiedenen Punkten der Struktur bei freien Schwingungen liefert. Wenn die Verschiebungen in zwei Punkten also unterschiedliche Phasenwinkel haben, erreichen sie ihre Maximalwerte nicht gleichzeitig.
In den meisten Fällen sind die Auswirkungen der Dämpfung auf die Modenformen und Eigenfrequenzen gering. Der Hauptgrund für die Einbeziehung der Dämpfung in eine Eigenfrequenzanalyse besteht darin, abzuschätzen, wie stark die verschiedenen Resonanzen gedämpft werden.
Frequenzganganalyse
Wenn die Anregungsfrequenz in der Nähe einer Eigenfrequenz liegt (z.B. innerhalb von ±50%), ist das Dämpfungsmodell von größter Bedeutung, wie die Antwortkurven im vorherigen Blog-Beitrag zeigen. Dies ist ein Fall, in dem Sie sich wirklich Mühe geben müssen, um angemessene Werte für die Dämpfung zu erhalten. In der Nähe der Resonanz werden die Ergebnisse vollständig von der Dämpfung bestimmt, so dass die Wahl zwischen einem Verlustfaktor von 0,01 oder 0,02 am Ende einen Faktor 2 bei einer Spannungsvorhersage bedeuten kann.
Analyse im Zeitbereich
Bei einer Analyse im Zeitbereich hat die Dämpfung in den meisten Fällen nur einen geringen Einfluss auf die Ergebnisse. Ausnahmen sind die Simulation der Wellenausbreitung oder wenn durch den zeitlichen Verlauf der Lasten einige Resonanzen stark angeregt werden.
Es gibt jedoch noch einen weiteren wichtigen Aspekt der Dämpfung in der Analyse im Zeitbereich: Sie kann die Zeitschritte stabilisieren. Es kommt häufig vor, dass unerwünschte, weniger interessante Wellen in der Struktur erzeugt werden. Wenn sie nicht richtig unterdrückt werden, können die Zeitschritte unnötig klein werden. Um solche Wellen zu unterdrücken, ist es von Vorteil, ein Dämpfungsmodell einzuführen, das vor allem bei hohen Frequenzen eine signifikante Dämpfung bietet.
Analyse des Antwortspektrums
Bei der Analyse des Antwortspektrums ist die Dämpfung Teil des Design-Antwortspektrums, so dass sie nicht explizit modelliert werden sollte. Ein einziger Dämpfungswert wird verwendet, um die gesamte Struktur zu repräsentieren.
Numerische Dämpfungsmodelle
Die Finite-Elemente-Formulierung
In Matrixform können die durch Finite-Elemente diskretisierten Bewegungsgleichungen wie folgt geschrieben werden:
wobei M die Massenmatrix, C die viskose Dämpfungsmatrix, K die Steifigkeitsmatrix, u der Verschiebungsvektor und die rechte Seite der Kraftvektor f ist.
Die Massen- und Steifigkeitsmatrizen werden anhand der Geometrie und der grundlegenden Materialparameter wie Massendichte und Elastizitätsmodul berechnet. Die Dämpfungsmatrix kann jedoch auf viele verschiedene Weisen gebildet werden. Oft können auch verschiedene Arten von Dämpfungsbeiträgen kombiniert werden.
Im Frequenzbereich, in dem angenommen wird, dass Anregung und Antwort harmonisch sind, lautet die entsprechende Gleichung
Hier sind die Verschiebungs- und Kraftvektoren komplexwertig.
Verlustfaktor-Dämpfung
Die Verlustfaktor-Dämpfung ist die wichtigste Methode zur Beschreibung von Verlusten im Material in einer Analyse im Frequenzbereich. Die mathematische Beschreibung erfolgt, wie im vorherigen Blog-Beitrag beschrieben, durch einen komplexwertigen Multiplikator zur Steifigkeit.
In COMSOL Multiphysics® können Sie die Verlustfaktor-Dämpfung über den Unterknoten Damping unter einem Materialmodell berücksichtigen. Für das Linear Elastic Material können Sie sogar individuelle Verlustfaktoren für die verschiedenen Elemente in der konstitutiven Matrix angeben.
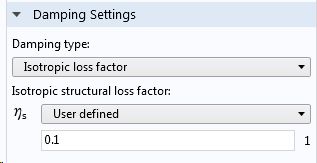
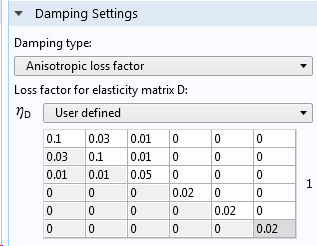
Eingabe von Werten für die Verlustfaktor-Dämpfung.
In der Realität ist es üblich, dass der Verlustfaktor eine gewisse Frequenzabhängigkeit aufweist. In einer Frequenzanalyse kann dies leicht berücksichtigt werden, indem Sie den Verlustfaktor zu einer Funktion der integrierten Variable freq machen. Sie können entweder einen Ausdruck verwenden, wie unten gezeigt, oder eine beliebige Funktion der Frequenz angeben.
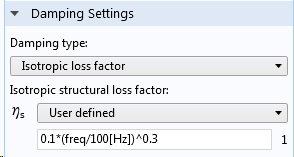
Frequenzabhängiger Verlustfaktor.
Um zu sehen, wie die Verlustfaktor-Dämpfung in das Gleichungssystem eingeht, nehmen Sie an, dass überall derselbe Verlustfaktor verwendet wird. Dann kann die Dämpfungsmatrix wie folgt identifiziert werden:
Die Bewegungsgleichung wird dann zu
Viskose Dämpfung
In einem Modell der viskosen Dämpfung treten im festen Material Spannungen auf, die proportional zur Dehnungsrate sind. Im allgemeinsten Fall kann der konstitutive Tensor, der die Spannung mit der Dehnungsrate verbindet, 21 unabhängige Konstanten enthalten. Da die Dämpfung nur schwer zu messen und zu quantifizieren ist, sind diese Werte nur selten bekannt, und es ist üblich, mit isotropen viskosen Dämpfungsmodellen zu arbeiten.
Die viskose Dämpfung im Interface Solid Mechanics in COMSOL Multiphysics® verwendet zwei Konstanten:
- Volumenviskosität,
- Scherviskosität,
Die erstere sorgt für eine Dämpfung, die proportional zur Volumenänderung ist, die letztere zur Formänderung.
Der viskose Spannungstensor kann wie folgt formuliert werden:
wobei die volumetrische Dehnung und
der deviatorische Teil des Verzerrungstensors ist.
Da die Dämpfungsspannung proportional zur Dehnungsrate ist, ist sie bei höheren Frequenzen stärker ausgeprägt.
Die viskose Dämpfung ist eine weitere Option im Knoten Damping.
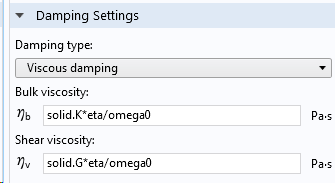
Angabe der viskosen Dämpfung.
Die viskose Dämpfung kann in jeder Art von dynamischer Studie verwendet werden.
Rayleigh-Dämpfung
Die Rayleigh-Dämpfung ist eine einfache Möglichkeit, eine Dämpfungsmatrix als reine Linearkombination der Massen- und Steifigkeitsmatrizen zu erzeugen:
Dieses Dämpfungsmodell hat keine direkte Verbindung zu physikalischen Dämpfungsprozessen. Ursprünglich wurde es eingeführt, weil es eine Dämpfungsmatrix liefert, die durch die Eigenmoden aus dem ungedämpften Eigenfrequenzproblem diagonalisiert werden kann und so eine vollständige dynamische Entkopplung zwischen den verschiedenen Moden ermöglicht.
Der Term der Steifigkeitsmatrix („Beta-Dämpfung“) kann jedoch so interpretiert werden, dass er direkt proportional zur Dehnungsrate ist. Tatsächlich entspricht eine reine Beta-Dämpfung einer viskosen Dämpfung mit
wobei K der elastische Kompressionsmodul und G der Schubmodul ist.
Die Beta-Dämpfung bietet, genau wie die viskose Dämpfung, eine stärkere Dämpfung bei höheren Frequenzen. Der massenproportionale Term α sorgt dagegen für eine starke Dämpfung bei niedrigen Frequenzen. Er wirkt auf die Geschwindigkeit der Struktur, dämpft also eine Starrkörperbewegung.
Die Rayleigh-Dämpfung wird auch im Unterknoten Damping unter einem Materialmodell angegeben. Dieses Design bietet die Freiheit, eine Art von Dämpfung zu erstellen, die eine Verallgemeinerung der ursprünglichen Rayleigh-Dämpfung ist. Damit die Dämpfungsmatrix eine lineare Kombination aus den Massen- und Dämpfungsmatrizen auf Systemebene ist, müssen die Rayleigh-Dämpfungsparameter in allen Damping-Knoten gleich sein. Ist dies nicht der Fall, gilt diese Eigenschaft nur für die Elementebene.
Es gibt zwei Möglichkeiten, wie Sie die Rayleigh-Dämpfungsparameter angeben können, entweder als direkte Angabe von α und β oder durch Angabe des Dämpfungsverhältnisses bei zwei verschiedenen Frequenzen.
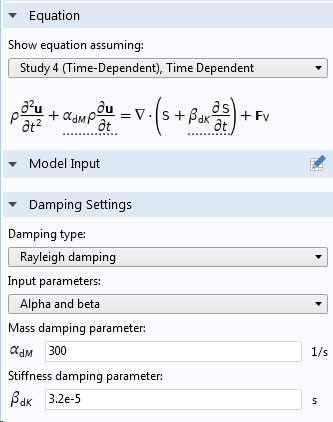
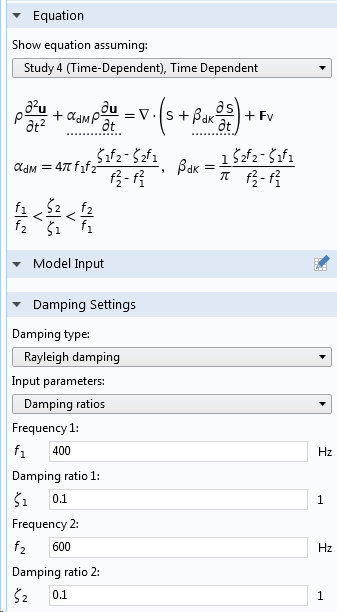
Angabe der Rayleigh-Dämpfung in einem Damping-Knoten zu einem Materialmodell.
Dissipative Materialmodelle
Einige Materialmodelle enthalten eine Dissipation. In diesem Zusammenhang ist der interessanteste Fall wahrscheinlich die Viskoelastizität. Wenn Sie ein solches Materialmodell verwenden, bietet es normalerweise eine erhebliche Dämpfung. In den meisten Fällen würden Sie es nicht mit einem Damping-Knoten auf demselben Gebiet kombinieren.
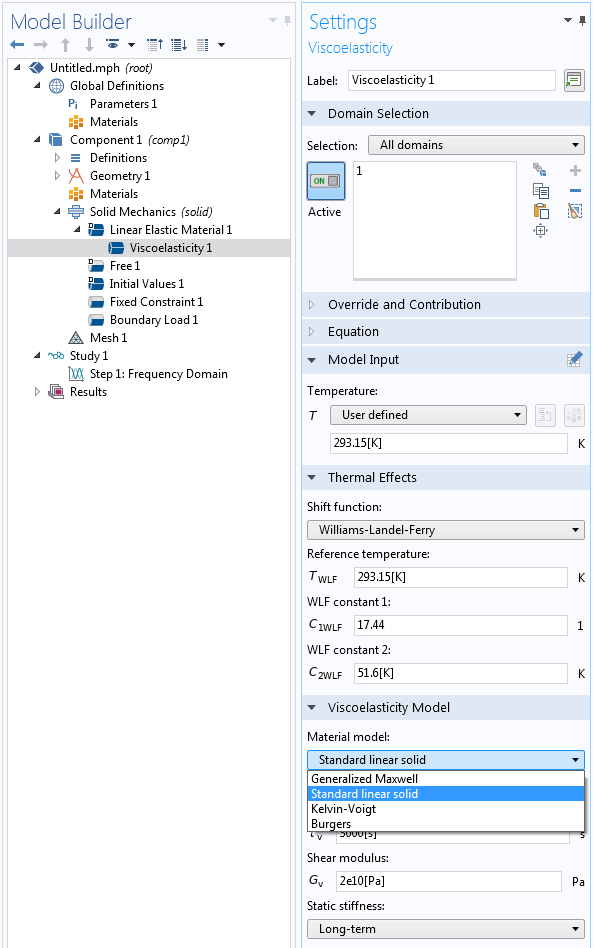
Auswahl eines viskoelastischen Materialmodells.
Thermoelastische Dämpfung
Die thermoelastische Dämpfung kann über die Multiphysik-KopplungThermal Expansion direkt in ein Modell einbezogen werden.
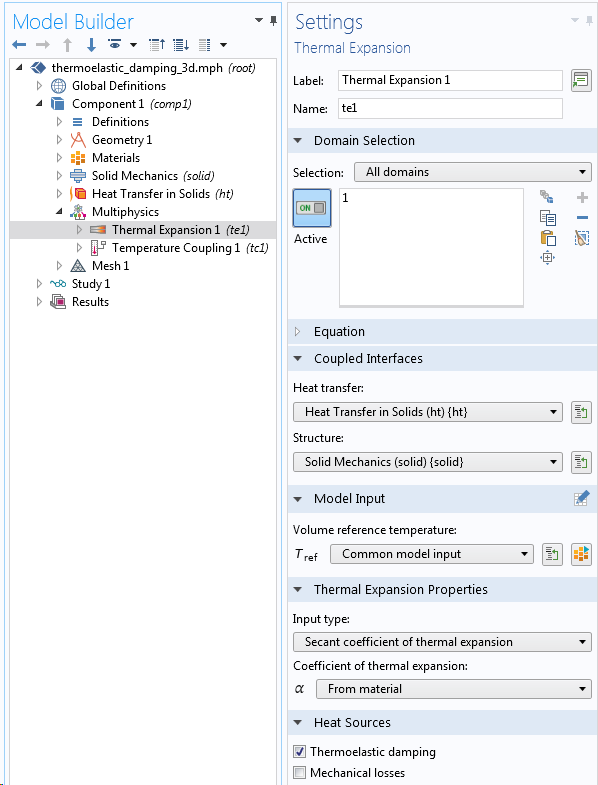
Thermoelastischen Dämpfung in einer gekoppelten Wärmetransport-Strukturmechanik-Analyse.
Der Effekt des Einbeziehens der thermoelastischen Dämpfung ist, dass ein Wärmequellen-Term, der proportional zur Änderungsrate der Spannung ist, zu den Wärmebilanzgleichungen hinzugefügt wird:
Hier ist T die Temperatur, der Spannungstensor und
der Koeffizient des thermischen Ausdehnungstensors.
Modale Dämpfung
Die Lösung von Problemen der linearen Strukturdynamik mit modaler Superposition ist eine sehr effiziente Technik. Wenn Sie die modale Superposition zusammen mit Dämpfung verwenden, gibt es einige Punkte zu beachten.
Die anfängliche Eigenfrequenzanalyse sollte mit dem ungedämpften Problem durchgeführt werden, und die Dämpfung wird erst während der modalen Superposition einbezogen. Dies lässt sich am einfachsten über den Abschnitt Physics and Variables Selection in den Einstellungen für jeden Studienschritt sicherstellen.
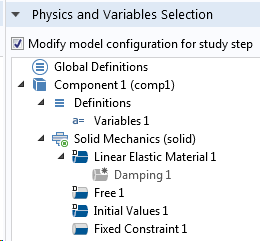
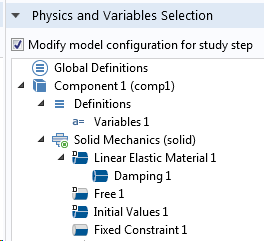
Einstellungen der Studienschritte für die Eigenfrequenzstudie (links) und die anschließende Modale-Superpositions-Studie (rechts).
Alle Arten von Dämpfungsbeiträgen sind in der modalen Superposition erlaubt. Dies mag nicht überraschend klingen, aber es ist ein Effekt der Tatsache, dass die Eigenmoden in den modalen Lösern in COMSOL Multiphysics® nicht als entkoppelt angesehen werden. Das bedeutet, dass Sie ein breiteres Spektrum an gedämpften Problemen lösen können als in vielen anderen Implementierungen einer Modalen-Superpositions-Methode.
Zusätzlich zur Dämpfung durch verschiedene physikalische Eigenschaften können Sie auch ein Dämpfungsverhältnis für jede Eigenmode angeben: Die sogenannte modale Dämpfung. Die modale Dämpfung ist besonders nützlich, wenn Sie aus Erfahrung wissen, dass einige Moden stärker gedämpft werden als andere. Dies ist der Fall, wenn verschiedene physikalische Phänomene mit den Modenformen verbunden sind. Die modale Dämpfung wird direkt in den Einstellungen für den modalen Löser angegeben.
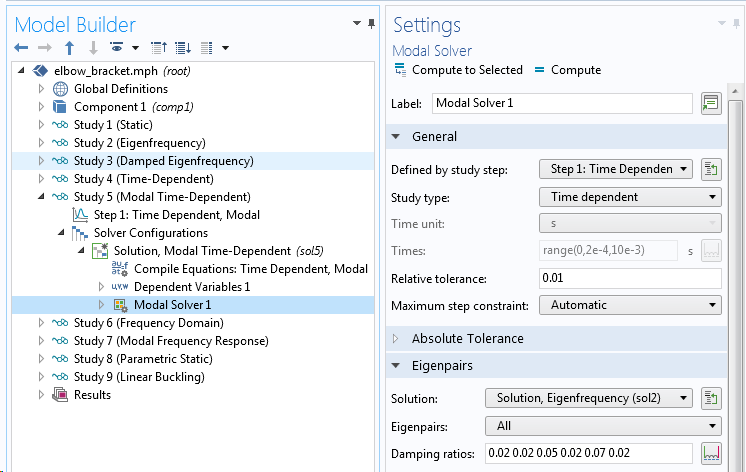
Angabe der modalen Dämpfung.
Die modale Dämpfung wird zu allen anderen Dämpfungsbeiträgen addiert.
Unendlichkeitsrandbedingungen
Wenn Sie Verluste durch Schallemissionen oder Ankerverluste modellieren, ist es wichtig, Ihr Modell mit Randbedingungen auszustatten, die ausgehende Wellen ohne Reflexion verschwinden lassen. COMSOL Multiphysics® bietet hier mehrere Optionen, abhängig von den beteiligten Physik-Interfaces und davon, ob die Analyse im Zeit- oder im Frequenzbereich erfolgt.
Im Frequenzbereich ist ein Perfectly Matched Layer (PML) eine gute Alternative für eine Randbedingung in Richtung „Unendlichkeit“. Die PML-Formulierung, die für viele verschiedene Physik-Interfaces verfügbar ist, dämpft im Wesentlichen ausgehende Wellen, so dass die reflektierte Energie sehr gering ist. Der Effekt ist, dass die Analyse gedämpft wird, da die Energie der ausgehenden Wellen verloren geht.
Ein PML wird mit einigen Schichten von Elementen auf der Außenseite des Berechnungsgebiets modelliert.
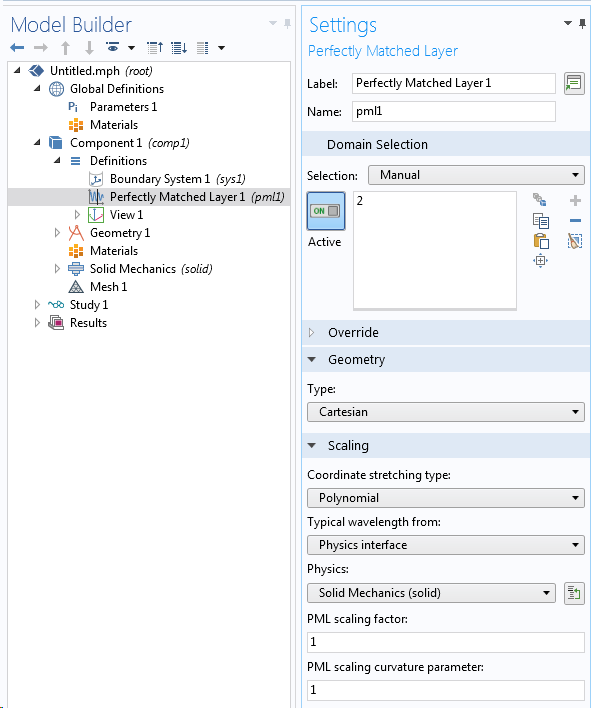
Definition eines Gebiets als PML.
Im Interface Solid Mechanics finden Sie auch eine spezielle Art von Randbedingung, die Low-Reflecting Boundary genannt wird. Ihr Zweck ist der gleiche wie bei einem PML: Die Vermeidung von Wellenreflexion. Obwohl er nicht so effizient ist wie ein PML, wenn die Wellen in einem schrägen Winkel auf die Ränder treffen, hat der Low-Reflecting Boundary-Knoten zwei Vorteile:
- Er kann für Analysen im Zeitbereich verwendet werden.
- Da es sich um eine Randbedingung handelt, ist es nicht nötig, zusätzliche Gebiete außerhalb des Berechnungsgebiets zu vernetzen.
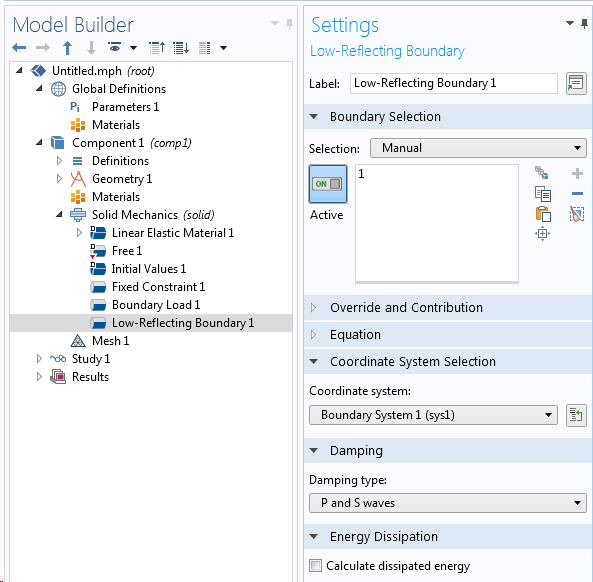
Der Knoten Low-Reflecting Boundary.
Eine andere Möglichkeit, Wellen zu simulieren, die sich ins Unendliche ausbreiten, ist die Anwendung der Randelemente-Methode (BEM) für akustische Wellen.
Reibung zwischen gleitenden Oberflächen
Wenn die Reibung eine wichtige Quelle der Dämpfung ist, müssen Sie oft einige technische Näherungen vornehmen. Im Prinzip können Sie natürlich ein zeitabhängiges Problem mit einer vollständigen Kontaktmodellierung einschließlich Reibung lösen. Leider ist dies in den allermeisten Fällen mit einem unverhältnismäßig hohen Aufwand an Computerressourcen verbunden.
Eine Alternative besteht darin, die Kontaktzone durch eine dünne elastische Schicht zu ersetzen und diese mit einer viskosen Dämpfung oder einem Verlustfaktor auszustatten. Die Frage ist jedoch, wie man die Schubsteifigkeit und den entsprechenden Verlustfaktor schätzt. Allgemeine Methoden zur Schätzung dieser Parameter sind ein Thema aktueller und laufender Forschungsarbeit. Möglicherweise müssen Sie erste lokale Analysen der Verbindung durchführen, um ihre Eigenschaften zu untersuchen.
Dämpfung in anderen Features
Neben den Materialmodellen gibt es viele weitere Funktionen, mit denen Sie Ihr Modell mit Dämpfung versehen können. Einige Beispiele sind:
- Das Feature Spring Foundation
- Das Feature Thin Elastic Layer
- Das Feature Spring-Damper
- Die Verbindungen und Getriebe im Interface Multibody Dynamics
- Die Features Damper und Impedance im Interface Lumped Mechanical System
- Die Lager in den Interfaces Rotordynamics und Multibody Dynamics
- Jede Last, die als geschwindigkeitsabhängig angegeben wird
- Komplexwertige Materialdaten
Abschließende Bemerkungen
Die Modellierung der Dämpfung in der Strukturdynamik ist ein wesentlicher und nicht trivialer Teil der Modelldefinition. COMSOL Multiphysics® bietet Ihnen eine breite Palette von Optionen zur Beschreibung der Dämpfung. Die Beschaffung der richtigen Daten für die Materialien und Komponenten einer Struktur ist jedoch oft eine Herausforderung.
Nächste Schritte
Erfahren Sie mehr über das Structural Mechanics Module, das spezielle Funktionen für die Modellierung der Dämpfung enthält:
- Lesen Sie Teil 1 dieser Blog-Serie: Dämpfung in der Strukturdynamik: Theorie und Quellen
- Wenn Sie sich für die Modellierung der Dämpfung interessieren, finden Sie in der Application Gallery einige Beispiele für verschiedene Ansätze:
- Static and Eigenfrequency Analyses of an Elbow Bracket
- Viscoelastic Structural Damper — Transient Analysis
- Bracket — Transient Analysis (bracket_frequency.mph)
- Wave Propagation in Rock Under Blast Loads
- Piezoelectric Tonpilz Transducer
- Thermoelastic Damping in a MEMS Resonator
- Disc Resonator Anchor Losses
- Vibrating Micromirror with Viscous and Thermal Damping: Transient Behavior




Kommentare (0)