Die Parameterschätzung bei nichtlinearen Materialmodellen in COMSOL Multiphysics®
Mechanische Systeme enthalten oft Komponenten, die ein nichtlineares Materialverhalten aufweisen. Beispiele hierfür sind große elastische Verformungen in Dichtungen, die Abhängigkeit von der Dehnungsrate und Hysterese bei zyklischer Belastung in Gummimaterialien und weichem biologischen Gewebe und elastoplastisches Fließen und Kriechen in Metallen. Zusammen mit dem Add-On Nonlinear Structural Materials Module enthält die Software COMSOL Multiphysics® mehr als hundert eingebaute Materialmodelle, mit denen hochkomplexes Materialverhalten modelliert werden kann. Ein Nachteil dieser oft phänomenologischen Modelle ist jedoch, dass sie eine große Anzahl von Materialparametern enthalten können, die für jedes spezifische Material kalibriert werden müssen, um genaue Modellvorhersagen zu erhalten. In unserem heutigen Blog-Beitrag zeigen wir, wie diese Parameter anhand von experimentellen Daten aus gängigen Materialtests mit Hilfe der Methode der kleinsten Quadrate in einem nichtlinearem Minimierungsverfahren geschätzt werden können.
Gängige Materialtests
Der Ausgangspunkt für die Schätzung von Materialparametern ist die Beschaffung relevanter experimenteller Daten. Was als relevant anzusehen ist, hängt weitgehend vom Materialtyp und der Art der zu erwartenden Belastungen in der endgültigen Anwendung ab, wie in einem vorherigen Blog-Beitrag erörtert wurde. So kann beispielsweise ein isotropes linear-elastisches Material mit einem einzigen uniaxialen Test charakterisiert werden. Materialien, die eine Abhängigkeit von der Dehnungsrate und der Belastungsgeschichte aufweisen, erfordern weitere Experimente, wie Relaxations-, Kriech- oder zyklische Tests bei unterschiedlichen Dehnungsraten. Wird die Komponente bei hohen und/oder variablen Temperaturen betrieben, muss möglicherweise auch die Temperaturabhängigkeit der Materialeigenschaften berücksichtigt werden.
Bei Materialien, die großen Verformungen ausgesetzt sind, ist es auch wichtig, das Material unter verschiedenen Spannungszuständen zu testen, selbst wenn das Materialverhalten isotrop ist. Obwohl es verlockend sein kann, ein hyperelastisches Modell an einem einzigen uniaxialen Test zu kalibrieren, wie es für lineare Elastizität üblich ist, kann die Vorhersage eines solchen Modells unter Druck- oder biaxialer Belastung zu unerwartetem oder sogar instabilem Materialverhalten führen. Stattdessen wird zur Kalibrierung gummiartiger Materialien üblicherweise eine Kombination von Experimenten durchgeführt, die uniaxiale Zug-, reine Scher- und äquibiaxiale Zugversuche umfasst. Im Folgenden werden Beispiele für die Durchführung solcher Experimente für Proben einer dünnen Gummiplatte gezeigt.
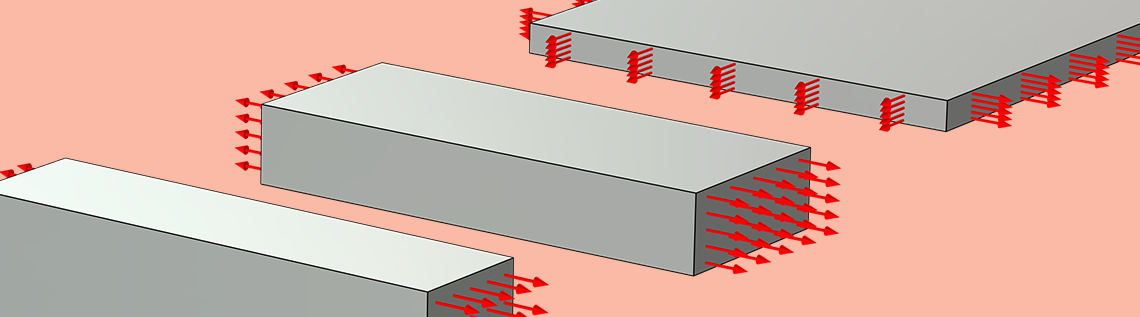
Von links nach rechts: Uniaxiale Zug-, reine Scher- und äquibiaxiale Aufblasversuche an einer dünnen Gummiplatte. Die roten Pfeile zeigen die vorgeschriebene Verschiebung und, beim Aufblasversuch, den angewandten Aufblasdruck.
Bei gut gewähltem Seitenverhältnis der Proben führen die oben gezeigten Konfigurationen zu homogenen Spannungs- und Dehnungszuständen in der Mitte der Proben. Diese können aus messbaren Größen, wie den angewandten Verschiebungen und Reaktionskräften oder dem angewandten Druck und dem Krümmungsradius der aufgeblasenen Membran, abgeschätzt werden. Materialtests, die zu homogenen Spannungs- und Dehnungszuständen führen, eignen sich besonders gut für die Parameterschätzung, da sie mit einem einzigen Element modelliert werden können, was den Rechenaufwand erheblich reduziert.

Von links nach rechts: Äquivalente homogene uniaxiale Zug-, reine Scher- und äquiaxiale Zugbelastung.
Nichtlineare Parameterschätzung nach der Methoden der kleinsten Quadrate
Wenn wir experimentelle Daten und ein Materialmodell zur Verfügung haben, müssen wir einen Optimierungsalgorithmus auswählen, der die aktuelle Modellvorhersage mit den Daten vergleicht und die Materialparameter aktualisiert, um die Differenz zu minimieren. Die Suche nach den unbekannten Materialparametern \mathbf{q}^* entspricht also der Lösung eines sogenannten inversen Problems. Dieses formulieren wir mathematisch als ein Problem der gewichteten kleinsten Quadrate,
bei dem \mathbf{W} eine Matrix von Gewichten und \mathbf{r} der sogenannte Defekt oder Residualvektor ist, der die Differenz zwischen den Modellvorhersagen, \mathbf{y}, und den experimentellen Daten, \hat{\mathbf{y}}, enthält. Die Modellvorhersage kann sowohl explizit als auch implizit von dem Materialparameter abhängen, das heißt, \mathbf{y} = \mathbf{y}(\mathbf{u}(\mathbf{q}), \mathbf{q}), wobei \mathbf{u} die Lösung des Vorwärtsproblems ist.
Zur besseren Veranschaulichung der verschiedenen Komponenten des Kleinste-Quadrate-Problems kann die quadratische Form wie folgt erweitert werden:
Hierin ist Ndie Anzahl der Datensätze; Q_n und M_n bezeichnen jeweils den Kleinste-Quadrate-Fehler und die Anzahl der Datenpunkte des Datensatzes n; und P_n(\mathbf{q}; \lambda_m) und \hat{P}_{n,m} bezeichnen jeweils die Modellvorhersage und die experimentellen Daten. Der Parameter \lambda_m bezeichnet die unabhängige Variable für den Versuch, wie die Zeit oder die angewandte Dehnung. Außerdem haben wir angenommen, dass \mathbf{W}eine Diagonalmatrix mit den Komponenten 1/s_{n,m}^2 ist, wobei s_{n,m} Skalierungsfaktoren sind, die die verschiedenen Datenpunkte und Datensätze gewichten und sicherstellen, dass die Größe dimensionslos ist. Das Kleinste-Quadrate-Problem kann auch durch untere und obere Schranken für die Parameter erweitert werden, was zur Auschließung von nichtphysikalischen Bereichen des Parameterraums, in denen das Materialmodell instabil ist, genutzt werden kann.
In COMSOL Multiphysics® stehen mehrere Optimierungsalgorithmen zur Lösung von Kleinste-Quadrate-Problemen zur Verfügung. In den meisten Fällen ist die Zielfunktion eine gutartige Funktion der Parameter und das Problem kann mit dem gradientenbasierten Levenberg-Marquardt-Algorithmus effizient gelöst werden. Kurz gesagt aktualisiert die Levenberg-Marquardt-Methode die Parameter iterativ, indem sie adaptiv zwischen einem Aktualisierungsschritt in Richtung des Gradientenabstiegs bei großer Entfernung vom Minimum und einem Gauß-Newton-Schritt näher am Minimum, wo nahezu quadratische Konvergenz erreicht werden kann, abwechselt. Eine wesentliche Größe im Aktualisierungsalgorithmus ist die Jacobi-Matrix
welche die Empfindlichkeit der Modellvorhersage gegenüber Änderungen an den Materialparametern misst. Die Bewertung der Jacobi-Matrix kann im Prinzip innerhalb des Optimierungslösers analytisch durchgeführt werden; wenn das Problem jedoch hochgradig nichtlinear und das Vorwärtsmodell kostengünstig zu bewerten ist, kann eine Finite-Differenzen-Approximation der Jacobi-Matrix im Hinblick auf Robustheit und Effizienz oft vorzuziehen sein. Wenn die Jacobi-Matrix nicht korrekt berechnet werden kann, z. B. wenn die Zielfunktion nicht differenzierbar ist, ist der gradientenfreie Algorithmus Bound Optimization by Quadratic Approximation (BOBYQA) eine Alternative, die keine explizite Berechnung der Ableitungen erfordert.
Optional kann der Levenberg-Marquardt-Löser in COMSOL Multiphysics® auch Konfidenzintervalle sowie die vollständige Kovarianzmatrix als Maße für die Unsicherheit der geschätzten Parameter berechnen. Dies kann besonders nützlich sein, wenn Sie Varianz in den experimentellen Daten haben, die Sie auf die Materialparameter übertragen wollen. Weitere Informationen finden Sie im Tutorial Parameter Estimation with Covariance Analysis.
Beispiele für die Schätzung nichtlinearer Materialparameter
In einem früheren Blog-Beitrag haben wir untersucht, wie Materialparameter für hyperelastische Modelle mit Hilfe analytischer Ausdrücke der Spannungs-Dehnungs-Kurven, die für zwei häufige Lastfälle abgeleitet wurden, geschätzt werden können. Dieser Ansatz kann jedoch nicht ohne weiteres auf Modelle mit inelastischen Materialien ausgedehnt werden, für die es oft keine analytischen Lösungen in geschlossener Form gibt. Stattdessen können wir die eingebauten Materialmodelle in COMSOL Multiphysics® benutzen. Wir wollen diesen Ansatz für zwei Fälle demonstrieren: Hyperelastizität und Viskoplastizität mit großen Dehnungen.
Parameterschätzung für ein hyperelastisches Ogden-Modell
Im ersten Beispiel kalibrieren wir ein hyperelastisches Ogden-Modell an uniaxiale Zug-, reine Scher- und äquibiaxiale Zugdaten, die ein weiches Elastomer darstellen. Die Daten sind im Folgenden zu sehen.

Uniaxiale Zug-, reine Scher- und äquibiaxiale Zugdaten, die ein weiches Elastomer darstellen. Beachten Sie, dass die äquibiaxiale Spannung viel größer ist und daher an einer zweiten y-Achse dargestellt ist.
Wir gehen davon aus, dass das Elastomer inkompressibel ist, so dass die Dehnungsenergiedichte im Ogden-Modell wie folgt lautet:
Hier werden zwei Terme in der Funktion der Dehnungsenergiedichte berücksichtigt, so dass das Problem darin besteht, die vier unbekannten Materialparameter \mathbf{q} = (\mu_1, \alpha_1, \mu_2, \alpha_2) zu ermitteln, wie auf dem folgenden Bild zu sehen ist.
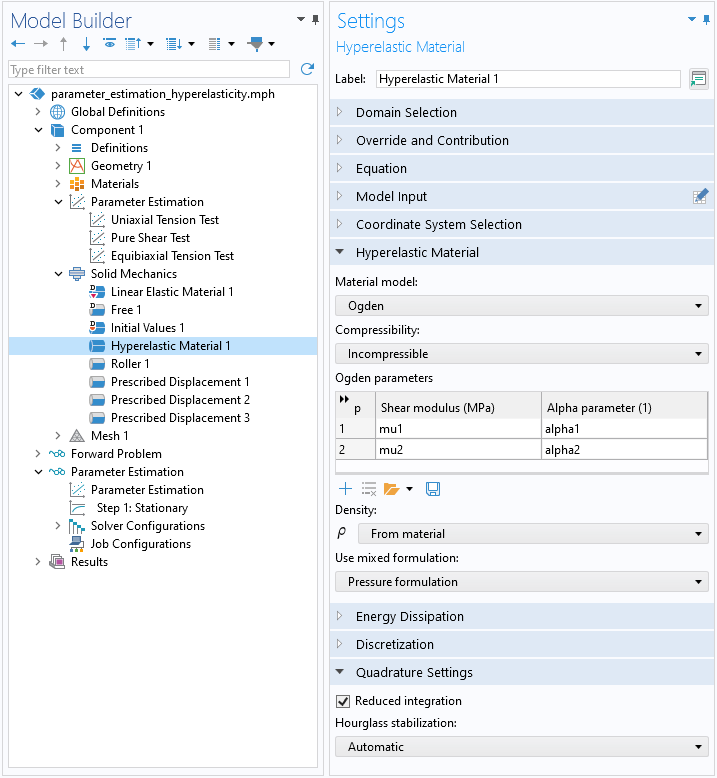
Einstellungen für das inkompressible Ogden-Modell mit zwei Termen. Beachten Sie, dass die reduzierte Integration zur Verringerung des Rechenaufwands verwendet werden kann, da die Lastfälle homogen sind.
Nach dem Einrichten des Materialmodells können wir die Datensätze in Ergebnistabellen importieren und sie mit den entsprechenden Modellausdrücken verknüpfen, indem wir die Features Global Least-Squares Objective verwenden. Die folgende Abbildung zeigt die Einstellungen für die aus den uniaxialen Daten gebildete Kleinste-Quadrate-Zielfunktion. Die Variable comp1.P_ua, die im Feld Model expression verwendet wird, ist als Volumenmittelwert der eingebauten Variablen für die Nennspannung, solid.PxX, definiert.

Die Einstellungen für das Feature Global Least-Squares Objective, das zu den uniaxialen Zugdaten gehört.
Im Studienschritt Parameter Estimation fügen wir die drei Zielfunktionen hinzu und geben die zu schätzenden Materialparameter an. In der Tabelle Estimated Parameters werden mu1 und alpha1 auf einen positiven Wert begrenzt, während mu2 und alpha2 auf einen negativen Wert begrenzt werden. Diese Grenzen stellen sicher, dass das Materialmodell die bekannten Stabilitätsanforderungen \mu_p\alpha_p > 0 für das Ogden-Modell erfüllt.

Die Einstellungen für den Studienschritt Parameter Estimation.
Der Lösungsfortschritt kann für jede Iteration des Optimierungslösers in einem Plot verfolgt werden, der die aktuelle Modellvorhersage mit den experimentellen Daten vergleicht. Wie in der folgenden Animation zu sehen ist, verbessert der Levenberg-Marquardt-Algorithmus innerhalb kurzer Zeit die Vorhersage des uniaxialen und des reinen Schermodells und nach einigen weiteren Iterationen auch die hochgradig nichtlineare äquibiaxiale Antwort.
Parameterschätzung eines viskoplastischen Bergstrom-Boyce-Modells
Im nächsten Beispiel betrachten wir das komplexere Bergstrom-Boyce-Materialmodell für viskoplastische Polymere, das sowohl eine Dehnungsrate als auch einen Belastungsverlauf und ein temperaturabhängiges Verhalten aufweist. Nachfolgend sind repräsentative Spannungs-Dehnungs-Kurven von zyklischen uniaxialen Zug- und Druckversuchen bei zwei verschiedenen Dehnungsgeschwindigkeiten und Raumtemperatur dargestellt.

Kurven der Be- und Entlastung bei uniaxialer Spannung und Kompression sowie zwei verschiedenen Dehnungsgeschwindigkeiten (0,1%/s und 10%/s) für ein repräsentatives Modell eines viskoplastischen Polymermaterials.
Das Bergstrom-Boyce-Materialmodell ist in COMSOL Multiphysics® Version 6.2 im Unterknoten Polymer Viscoplasticity des Features Hyperelastic Material verfügbar. Hier definiert das übergeordnete hyperelastische Modell ein elastisches Gleichgewichts-Netzwerk, während der Unterknoten ein paralleles Nichtgleichgewichts-Netzwerk hinzufügt, das sowohl ein elastisches als auch ein unelastisches Element enthält. In diesem Beispiel werden die elastischen Elemente mit der nahezu inkompressiblen Arruda-Boyce-Dehnungsenergiedichte modelliert, und sowohl Dehnungs- als auch Spannungsverfestigung werden in das viskoplastische Fließen einbezogen. Insgesamt enthält das Materialmodell sechs unabhängige Materialparameter, \mathbf{q} = (\mu_0^\textrm{eq}, N_\textrm{c}, \beta_\textrm{v}, A, c, n): der Schermodul des Gleichgewichts-Netzwerks, \mu_0^\textrm{eq}; die Anzahl der Kettensegmente, N_\textrm{c}; der Energiefaktor zwischen dem Nichtgleichgewichts- und dem Gleichgewichts-Netzwerk, \beta_\textrm{v}; der Koeffizient der viskoplastischen Flussrate, A; der Exponent der Dehnungsverfestigung, c; und der Exponent der Spannungsverfestigung, n.

Einstellungen für das Bergstrom-Boyce-Modell im Feature Polymer Viscoplasticity. Das Fenster Graphics zeigt Ein-Element-Modelle der uniaxialen Druck- und Zugversuche.
Wie bei der Hyperelastizität kann nun das Kleinste-Quadrate-Problem aufgestellt und gelöst werden. In der folgenden Animation ist zu sehen, dass bereits nach etwa 5 Iterationen eine visuell zufriedenstellende Lösung erzielt wird, obwohl der Optimierungslöser etwa 12 Iterationen bis zur Konvergenz benötigt. Das liegt daran, dass die voreingestellten Abbruchkriterien des Levenberg-Marquardt-Lösers prüfen, ob das Inkrement der Parameter oder der maximale Winkel zwischen dem Defektvektor und der Jacobi-Matrix kleiner als eine vorgegebene Optimalitätstoleranz ist. In den Einstellungen des Optimierungslösers können Sie optional ein auf der relativen Änderung des Defektvektors basierendes zusätzliches Abbruchkriterium einfügen, das nützlich sein kann, wenn der Löser ein relativ flaches lokales Minimum im Parameterraum erreicht, bei dem die Verbesserungen der Zielfunktion klein sind. Die voreingestellten Abbruchkriterien sind jedoch normalerweise robuster als ein Abbruch aufgrund einer Defektreduktion.
Testen der Stabilität Ihres Materialmodells
Nach der Parameterschätzung eines nichtlinearen Materialmodells ist es sinnvoll, das Materialmodell zu testen, um seine numerische Stabilität zu gewährleisten. Dieses Thema wird in Teil 2 dieser Serie ausführlich behandelt.
Schlusswort und weitere Lernmöglichkeiten
In diesem Blog-Beitrag haben wir gezeigt, wie man in COMSOL Multiphysics® die Parameter nichtlinearer Werkstoffmodelle anhand von Daten aus typischen Materialtests schätzen kann. Der vorgestellte Ansatz ist allgemein auf jede Art von Materialmodell und Materialtestdaten anwendbar.
Um die Parameterschätzung verschiedener Modelle mit Hilfe von Schritt-für-Schritt-Anleitungen selbst durchzuführen, sehen Sie sich die folgenden Modelle in der Application Gallery an:




Kommentare (0)