
Wollten Sie schon einmal die projizierte Fläche einer CAD-Datei berechnen? Das kann in vielen Fällen nützlich sein, z.B. für eine schnelle Abschätzung des Luftwiderstands. Wenn Sie nur an der projizierten Fläche entlang einiger weniger Richtungen interessiert sind, gibt es verschiedene Berechnungsmöglichkeiten, aber was ist, wenn Sie die projizierte Fläche über alle möglichen Richtungen berechnen möchten? Im Folgenden werden wir uns eine effiziente Methode zur Berechnung und Verwendung solcher Daten ansehen.
Einige einfache Ansätze
Stellen wir uns eine komplizierte CAD-Geometrie vor. Wir beginnen mit der Frage: Wie groß ist die projizierte Fläche dieser Geometrie entlang einer bestimmten Richtung? Es gibt mehrere Möglichkeiten, dies zu berechnen. Zunächst können wir den Operator General Projection verwenden. Bei diesem Ansatz muss ein Rahmen um die gesamte Geometrie gezogen und sehr fein vernetzt werden, um eine gute Auflösung zu erreichen. Aufgrund des Aufwands für die Vernetzung und Integration über das gesamte Gebiet kann dieser Ansatz sehr rechenintensiv sein. Der zweite Ansatz, neu in Version 6.0, ist die Verwendung der Funktion Projection of a 3D Model, mit der wir Arbeitsebenen im Raum zeichnen und die 3D-CAD-Datei darauf projizieren können. Die Flächen dieser Projektionen können direkt gemessen werden. Dieser CAD-basierte Ansatz ist viel schneller und erfordert keine Vernetzung, erfordert aber entweder das CAD Import Module, das Design Module, oder ein LiveLink™ Produkt. Beide Ansätze sind umständlich, wenn wir die projizierte Fläche entlang vieler verschiedener Richtungen berechnen wollen.
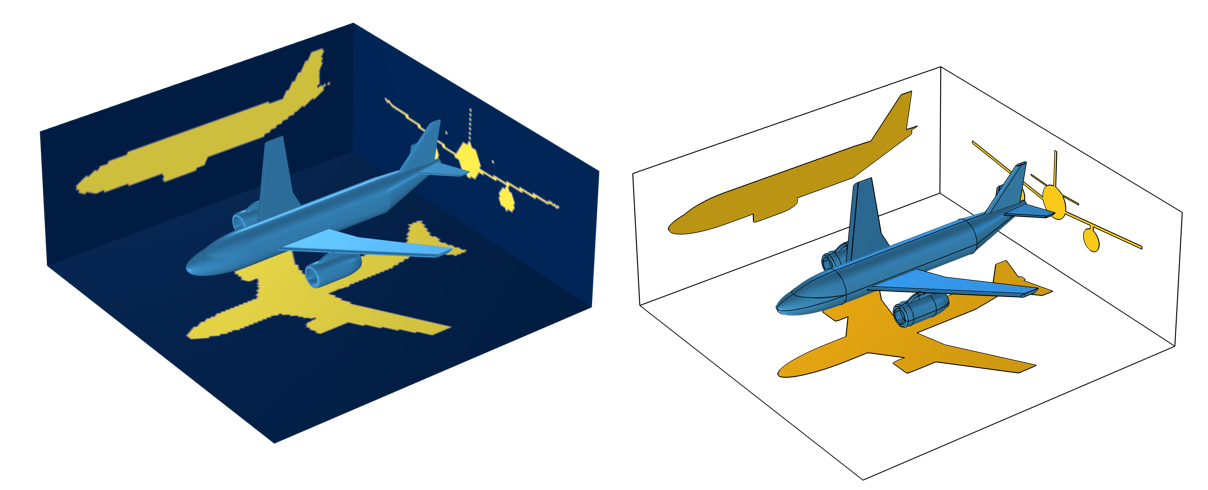
Zwei Möglichkeiten, die projizierte Fläche zu bestimmen: Über einen General Projection Operator, dessen Ergebnisse netzabhängig sind (links), und mit der Projection Funktionalität, die projizierte Flächen auf einem Set von Arbeitsebenen erzeugt (rechts).
Ein allgemeinerer Ansatz
Anstatt das Volumen der CAD-Datei zu vernetzen oder CAD-Operationen hinzuzufügen, können wir die Definition der projizierten Fläche nutzen. Sie lautet:
wobei der Winkel zwischen der Sichtlinie und der Normalen zur Oberfläche ist, für die Oberflächen, die entlang dieser Richtung sichtbar sind.
Ein Oberflächenintegral zu bilden ist einfach, aber wie können wir den Term auswerten? Es stellt sich heraus, dass wir diesen Term über das Interface Surface-to-Surface Radiation ermitteln, wenn wir eine externe Strahlungsquelle vom Typ Infinite Distance verwenden. Für die Berechnung ist lediglich ein Netz auf der Oberfläche des Bauteils erforderlich, nicht auf dem Volumen. Es ist nicht einmal notwendig, die Strahlung von Oberfläche zu Oberfläche zu berechnen, da der einfallende externe Fluss, einschließlich der Schatten, in einem Vorverarbeitungsschritt berechnet wird. Wir können also einfach den externen Fluss über alle Oberflächen integrieren, durch den einfallenden Nennfluss dividieren und erhalten die projizierte Fläche entlang der Richtung, die wir in das Feature External Radiation Source eingegeben haben. Da wir die Gauß-Integration vierter Ordnung verwenden, können wir relativ grobes Netz verwenden.
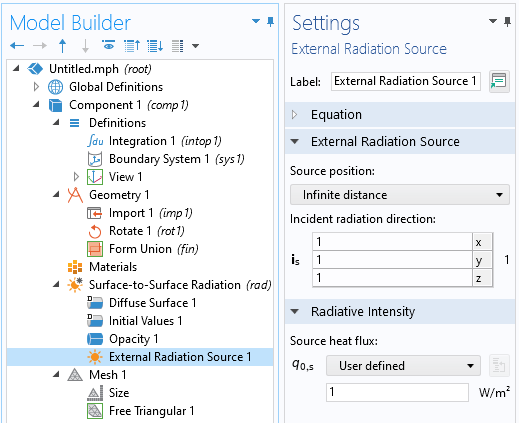
Das Feature External Radiation Source kann verwendet werden, um eine Beleuchtung einer Geometrie einzurichten, um die projizierte Fläche zu berechnen.
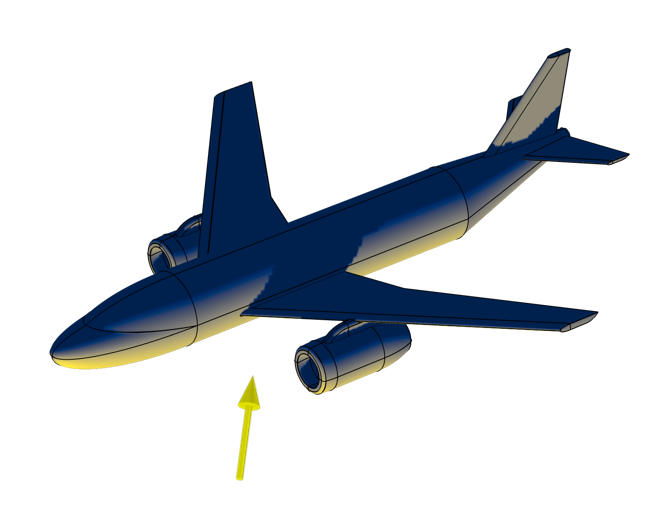
Der mit dem Feature External Radiation Source berechnete einfallende Strahlungsfluss kann integriert werden, um die projizierte Fläche zu erhalten. Man beachte den Schatten des Flügels
Extraktion und Verwendung von projizierten Flächen für alle Richtungen
Oft ist es notwendig, die projizierte Fläche aus allen Richtungen zu extrahieren. Wir könnten einfach das obige Integral für jede relevante Auftreffrichtung neu berechnen, aber das wäre rechnerisch sehr aufwendig.
Stattdessen stellen wir uns eine Kugel vor, die das Objekt umgibt, und wählen eine endliche Anzahl von Richtungen auf dieser Kugel, aus denen das Ziel beleuchtet werden soll. Zwischen diesen endlichen Richtungen können wir dann eine lineare Interpolation über die gesamte Kugeloberfläche durchführen. Bevor wir diese Richtungen auswählen, sollten wir jedoch bedenken, dass die projizierte Fläche symmetrisch zu jeder Ebene ist, die durch den Mittelpunkt der umgebenden Kugel verläuft, und dass die CAD-Geometrie, mit der wir hier arbeiten, symmetrisch zur Mittelebene ist. Es ist daher sinnvoll, diese beiden Symmetrien zu nutzen und nur eine Viertelkugel zu betrachten, die im positiven xy-Quadranten des Raumes liegt.
Als nächstes gehen wir die folgenden Schritte durch:
- Erstellung einer Geometrie, die die Symmetrie des CAD-Bauteils ausnutzt, mit einer begrenzten Anzahl von Punkten, die die Blickrichtungen definieren
- Berechnung der projizierten Querschnittsfläche entlang dieser Richtungen
- Interpolation der Daten auf alle Zwischenrichtungen
- Extraktion der Daten
Wir beginnen mit der Erstellung einer speziellen Geometrie, wie in der Abbildung unten gezeigt. Diese Geometrie sieht aus wie das Netz einer Viertelkugel und wird erzeugt, indem zunächst ein Netz eines Teils einer Einheitskugel separat erzeugt, dieses Netz exportiert und dann in eine zweite Komponente des Modells importiert wird. Die Importeinstellungen sind so gewählt, dass jedes Element des Oberflächennetzes eine eigene Oberfläche und jeder Knoten ein Geometriepunkt ist. Diese Fläche liegt im positiven xy-Quadranten des Raumes.
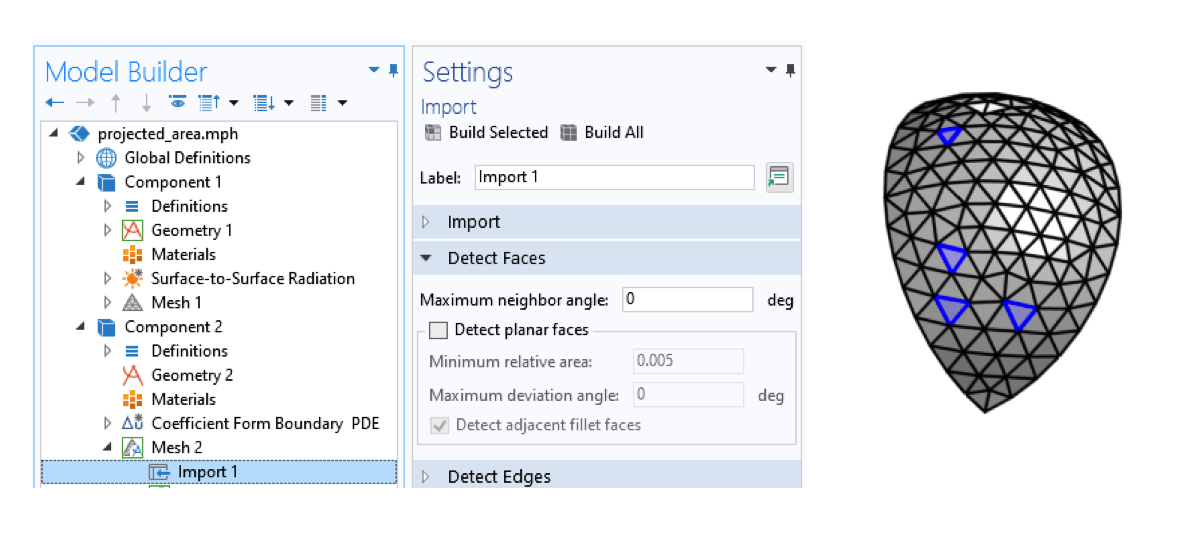
Import eines Netzes mit Einstellungen, bei denen jedes Element eine andere Fläche darstellt..
Jeder dieser Punkte repräsentiert eine der abgetasteten Richtungen, für die wir die projizierte Fläche auswerten werden. Für jedes Dreiecksfeld zwischen diesen Punkten wird die Oberfläche linear interpoliert, indem die linearen Finite-Elemente-Basisfunktionen verwendet werden, so dass wir die projizierte Oberfläche für jeden Einfallswinkel approximieren können.
Dazu fügen wir eine Coefficient Form Boundary PDE über alle Flächen unseres Viertelkugelmodells ein, setzen die Diskretisierung auf linear und den Namen der abhängigen Variablen auf AREA.
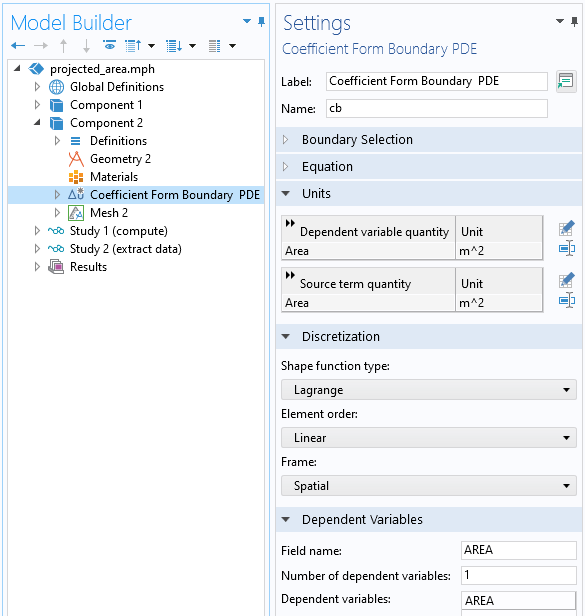
Einstellungen für das Interface Coefficient Form Boundary PDE , mit dem die Interpolation implementiert werden kann.
In diesem Interface wenden wir die Funktion Pointwise Constraint auf alle Punkte in der Geometrie an, was zur Folge hat, dass das Problem vollständig beschränkt wird, da alle Knotenpunkte auf Geometriepunkten liegen. Der Nettoeffekt dieser Einstellungen ist, dass alle anderen Physikeinstellungen keine Auswirkungen haben und auf ihren Standardwerten belassen werden können. Die Lösung, die wir erhalten, ist einfach eine lineare Interpolation zwischen den beschränkten Knotenwerten an den Ecken jeder Fläche.
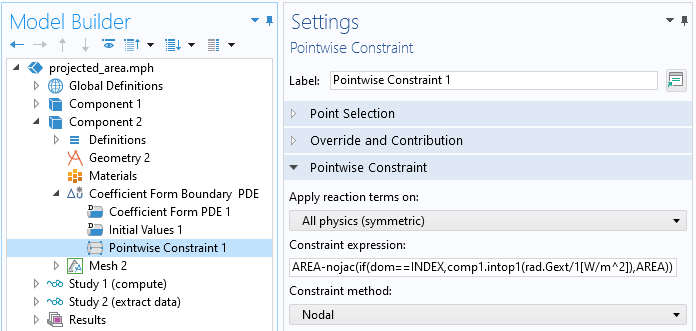
Anwenden von Pointwise Constraint auf alle Punkte des Modells.
Wir müssen also für jeden Punkt die projizierte Fläche in dieser diskreten Blickrichtung festlegen. Dazu verwenden wir den Bedingungsausdruck:
AREA-nojac(if(dom==INDEX,comp1.intop1(rad.Gext/1[W/m^2]),AREA))
Lassen Sie uns diesen Ausdruck, der den Wert von AREA an jedem Punkt festlegt, entschlüsseln. Zunächst muss der gesamte Ausdruck Null sein, also wird AREA gleich dem Ausdruck innerhalb des Operators nojac() gesetzt. Dieser Operator bedeutet, dass der darin enthaltene Ausdruck keinen Jacobi-Beitrag hinzufügt. Weitere Details hierzu finden Sie in unserem Blog-Beitrag über die Beschleunigung der Modellkonvergenz mit symbolischer Differenzierung. Innerhalb dieses Operators befindet sich der Ausdruck if(logical expression, true, false). Dieser Ausdruck beginnt mit dem logischen Ausdruck dom==INDEX. Jedes Geometrieobjekt (ein Gebiet, ein Rand, eine Kante oder ein Punkt) ist mit einer eindeutigen ganzen Zahl verknüpft: seinem Gebietsindex, dom. In der Studie, die wir gleich ausführen werden, werden wir einen Auxiliary Sweep über den globalen Parameter INDEX für alle Punkte in dieser Geometrie durchführen.
Während dieses Sweeps bleibt die Variable AREA einfach unverändert, wenn der logische Ausdruck als falsch bewertet wird. Wenn der logische Ausdruck wahr ist, erhalten wir die projizierte Fläche, das Integral des abgefangenen Flusses dividiert durch den einfallenden Fluss. Der Integrationsoperator comp1.intop1() ist in unserer ersten Komponente über alle exponierten Flächen der CAD-Datei definiert. Wenn dieses Integral jedoch ausgewertet wird, woher weiß dann das Feature External Radiation Source in der ersten Komponente, welche Richtung mit dem Punkt in der zweiten Komponente verbunden ist? Wir verwenden eine zweite Integralkopplungsvariable über alle Punkte in der zweiten Komponente und verwenden diese im Feld External Radiation Source für die Richtung:
comp2.intop2(x[1/m]*(dom==INDEX))
Dieser Ausdruck kann wie folgt gelesen werden: Werte alle Punkte in der zweiten Komponente, der x-Position (oder y– oder z-Position) und multipliziere mit (dom==INDEX), was null oder eins ergibt. Das bedeutet, dass wir nur für den aktuell indizierten Punkt den Beleuchtungsvektor auswerten, der auf diesen Punkt gerichtet ist, wie in der folgenden Abbildung gezeigt.
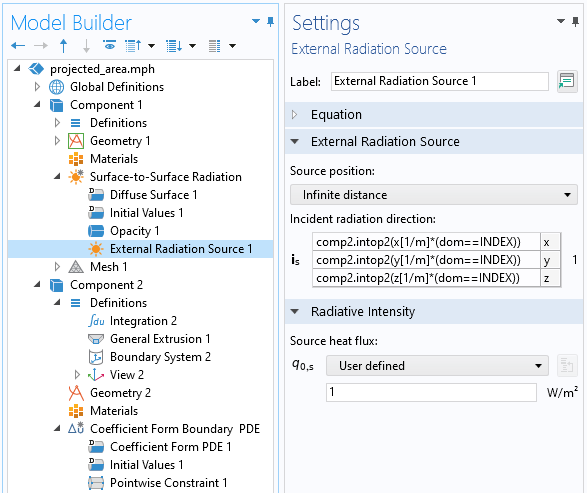
In der ersten Komponente wird die Richtung der einfallenden Strahlung auf der Grundlage der durch die Geometrie in der zweiten Komponente definierten Punktpositionen festgelegt.
Als nächstes wollen wir alle Werte unserer Indexvariablen durchgehen, was wir mit einem stationären Studienschritt machen, der einen Auxiliary Sweep enthält. In dieser Studie müssen wir die Strahlung von Oberfläche zu Oberfläche nicht lösen, da der einfallende Fluss ein Preprocessing-Schritt ist.
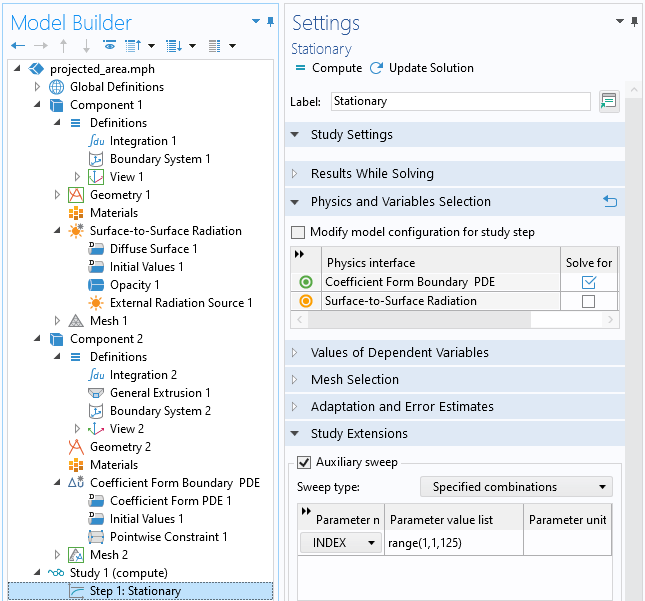
Wenn Sie einen Sweep über die Indexvariable durchführen, erhalten Sie die projizierte Fläche.
Da nur der letzte Wert im Sweep alle Ergebnisse enthält, können wir alles außer dieser letzten Lösung verwerfen. Dies können Sie über den Studienschritt Combine Solutions tun, wie in der folgenden Abbildung dargestellt.
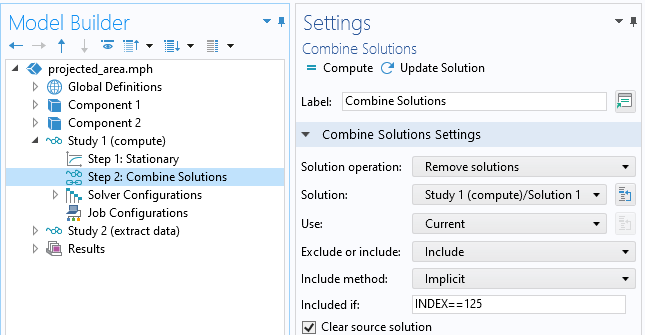
Verwendung des Features Combine Solutions, um nur die letzte Lösung im Sweep zu behalten.
Um ein Beispiel für die Verwendung dieser Daten zu geben, können wir eine zweite Studie mit einem zeitabhängigen Schritt verwenden, bei dem wir einen Punkt auf der Kugeloberfläche in einem sphärischen Koordinatensystem verfolgen, das mit der Flugzeugachse und der Aufwärtsrichtung ausgerichtet ist und die Winkel und
definiert.
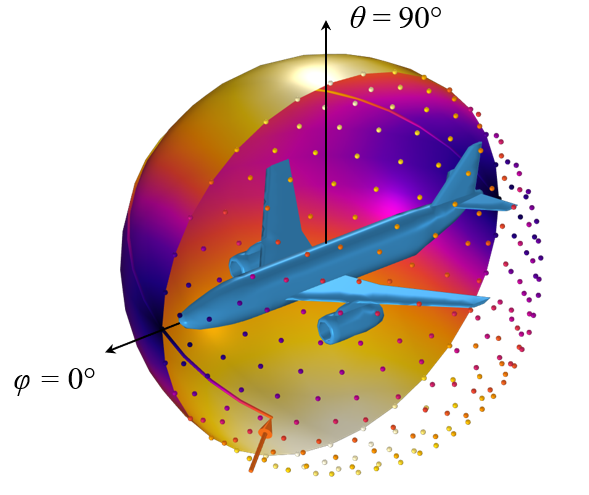
Das CAD-Modell und die projizierte Fläche entlang diskreter Richtungen, dargestellt durch eine Reihe von Punkten, sowie interpoliert über eine Fläche. Der Wert des Feldes entlang einer Linie, die über diese Fläche gezogen wird, kann über einen General Extrusion Operator in Bezug auf ein sphärisches Koordinatensystem ausgewertet werden.
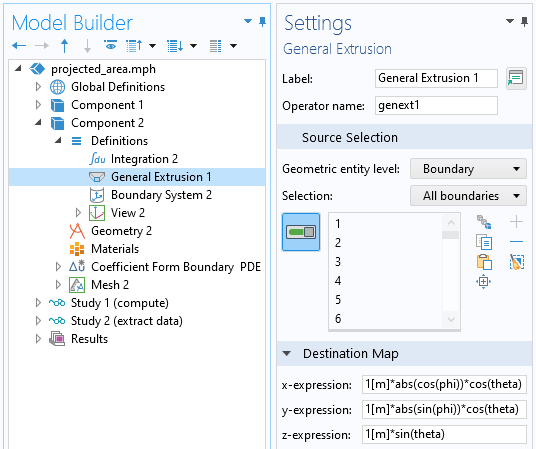
Extraktion der interpolierten Daten auf der Oberfläche der Kugel mithilfe des Operators General Extrusion.
Um Daten von einem beliebigen Punkt auf dieser Kugel im Sinne eines sphärischen Koordinatensystems zu extrahieren, können wir den Operator General Extrusion als dynamische Sonde verwenden, indem wir Variablen für die Destination Map-Ausdrücke eingeben, die die Symmetrie der Lösung berücksichtigen.
Abschließende Bemerkungen
Es gibt mehrere Möglichkeiten, die projizierte Fläche einer CAD-Datei zu berechnen. Von den drei hier vorgestellten Methoden ist die Verwendung des Operators General Projection die rechenintensivste, da sie über eine Fläche integriert und ein feines Netz im umgebenden Bereich erfordert. Er sollte daher nur verwendet werden, wenn die beiden anderen Ansätze nicht verwendet werden können. Der zweite Ansatz, der die Funktion Projection verwendet, ist eine CAD-basierte Operation. Sie ist einfach, genau und netzunabhängig, erfordert jedoch eine manuelle Einstellung für jede Projektionsrichtung. Der letzte Ansatz, die Verwendung des Interface Surface-to-Surface Radiation, ist am aufwendigsten einzurichten, bietet aber große Flexibilität bei der Wiederverwendung von Daten für weitere gleichungsbasierte Modellierungen. Die Datei, die diesen Ansatz veranschaulicht, kann hier heruntergeladen werden:




Kommentare (0)