
Wie die B-H-Kurve eine magnetische Analyse beeinflusst (und man wie sie verbessert)
Die B-H-Kurve wird im Allgemeinen verwendet, um das nichtlineare Verhalten der Magnetisierung zu beschreiben, das ein ferromagnetisches Material als Reaktion auf ein angelegtes Magnetfeld zeigt. In diesem Blog-Beitrag zeigen wir Ihnen, wie die B-H-Kurve Ihre magnetische Analyse beeinflusst und wie sie verbessert werden kann. Dazu verwenden wir eine Demo-App, die seit der Version 5.5 von COMSOL Multiphysics® verfügbar ist.
Die B-H-Kurve, Permeabilität und differentielle Permeabilität
Magnetische Weicheisenstähle werden häufig als Kernmaterial in Motoren, Transformatoren und Induktoren verwendet. Wenn sie in einem Bereich ohne Magnetfelder platziert werden, bleiben sie ohne Magnetfeld; sie haben keine “intrinsische” Magnetisierung. Die B-H-Kurve wird in der Regel zur Beschreibung der Magnetisierungseigenschaften solcher Materialien verwendet, indem die Permeabilität \mu charakterisiert wird, die wie folgt definiert ist:
wobei \mathbf{B} und \mathbf{H} die magnetische Flussdichte in Tesla (T) bzw. die magnetische Feldstärke in Ampère pro Meter (A/m) darstellen.
COMSOL Multiphysics® verfügt über mehr als 200 integrierte Materialien mit B-H-Kurven. Insbesondere die Nonlinear Magnetic Materialbibliothek deckt die meisten der weit verbreiteten nichtlinearen magnetischen Materialien ab. COMSOL Multiphysics® verwendet typischerweise eine Interpolationsfunktion mit einer lokalen Tabelle, um die B-H-Kurve zu definieren. Sie können auch Ihre eigenen B-H-Kurven einfügen, indem Sie die B-H Curve Materialeigenschaft zu einem neuen magnetischen Material hinzufügen.
Die B-H-Kurve eines Materials kann im Labor unter Berücksichtigung von bestimmten Normen und Verfahren gemessen werden. Es ist jedoch schwierig, eine direkte Messung durchzuführen, wenn \mathbf{B} über der Sättigung liegt, was als überströmter Bereich bezeichnet wird. Im Allgemeinen ist es für Prüfgeräte schwierig, einen so hohen Wert an konstantem \mathbf{B} zu erreichen; zum Beispiel 1,8 T. Selbst wenn die Prüfgeräte dazu in der Lage sind, sind die gemessenen Daten in der Regel ungenau, weil der Versuchsaufbau zu heiß wird. Aus diesem Grund werden die Daten der B-H-Kurve im Bereich der Sättigung in der Regel mit Hilfe von Extrapolationsmethoden ermittelt, z. B. mit der Methode der simultanen exponentiellen Extrapolation (SEE) (Ref. 1).
Aus numerischer Sicht ist die Steigung der B-H-Kurve von großer Bedeutung, da der nichtlineare iterative Löser sie verwendet, um die lokale Linearisierung des nichtlinearen Materialverhaltens auszuwerten. Daher ist es sinnvoller, die differentielle Permeabilität oder die inkrementelle Permeabilität zu berücksichtigen, insbesondere bei nichtlinearen magnetischen Materialien. Die differentielle Permeabilität ist definiert als:
Für Standardmaterialien ist \mu_D größer als 0, was bedeutet, dass die B-H-Kurve monoton steigend ist. Bei ferromagnetischen Materialien sinkt \mu_D nach der magnetischen Sättigung auf die Permeabilität des Vakuums \mu_0, wie in der folgenden Abbildung dargestellt.

Schematische Darstellung einer typischen B-H-Kurve und der entsprechenden differentiellen Permeabilität als Funktion der Magnetfeldstärke.
Wie sich die Extrapolation der B-H-Kurve auf die Simulation auswirkt
Im Settings Fenster der B-H Curve Interpolationsfunktion können Sie auf den Plot Button klicken, um sich die B-H-Kurve anzeigen zu lassen. Für eine bessere Visualisierung kann die Extrapolation auf Constant gesetzt werden. Diese Einstellung wird jedoch nicht für die Berechnung empfohlen, da die B-H-Kurve sonst an den Anfangs- und Endpunkten der Daten Unstetigkeiten aufweist.
Um zu verstehen, wie sich die Einstellung tatsächlich auf die Simulation auswirkt, nehmen wir das E-Core Transformer Tutorial Modell in der AC/DC Module Application Library als Beispiel. Die Berechnung braucht etwa zwei Minuten, wenn die Extrapolation der B-H-Kurve auf Constant und etwa eine Minute, wenn auf Linear gestellt wird für eine zeitabhängige Studie von 0 bis 0.05 s. Die Konvergenzdiagramme der beiden Simulationen erklären den Unterschied in der Berechnungszeit. Wie die folgende Abbildung zeigt, sind aufgrund der durch die Extrapolation-Einstellung verursachten Diskontinuitäten viel kleinere Zeitschritte erforderlich, um eine Lösung zu finden, wenn die Magnetisierung die Sättigung erreicht.
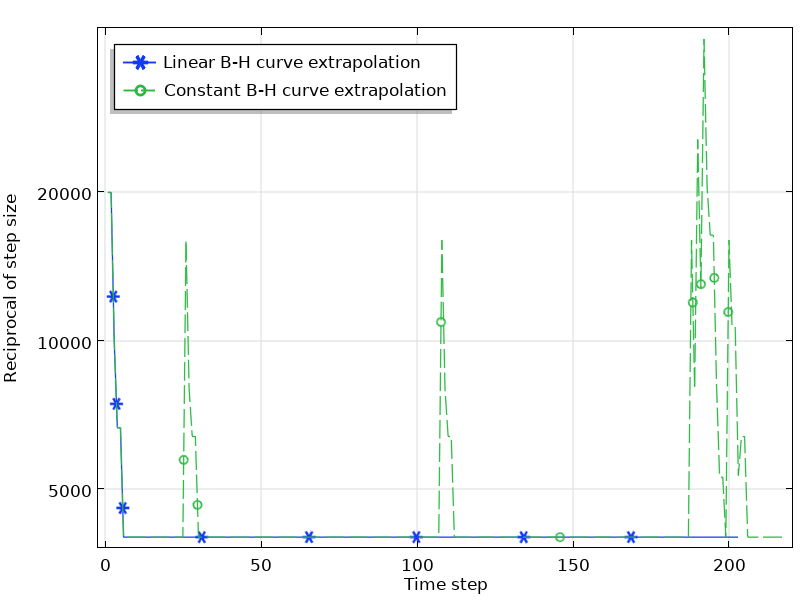
Die Konvergenzkurve der Simulation mit einer linearen und konstanten Extrapolation der B-H-Kurve.
Wie sich die Glätte der B-H-Kurve auf die Simulation auswirkt
Zusätzlich zu den Problemen der Extrapolation kann die \mu_D-Kurve aus gemessenen B-H-Daten Peaks enthalten, die im Allgemeinen unphysikalisch sind. Solche unphysikalischen Kurven verursachen numerische Instabilitäten, die zu längeren Berechnungszeiten oder zu keiner Konvergenz führen. Nehmen wir wieder das E-Core Transformer Modell als Beispiel. Das Modell verwendet das eingebaute Soft Iron-Material, bei dem die B-H-Kurve glatt ist. Jetzt ändern wir die Kurve, indem wir einige Datenpunkte ändern, um drei neue Arten von B-H-Kurven zu erstellen, siehe unten. Dann führen wir die zeitabhängige Studie im Modell mit diesen drei B-H-Kurven durch, wobei alle anderen Einstellungen gleich bleiben. Die Simulationsdetails sind in der Tabelle unten aufgeführt und die Konvergenzdiagramme sind in der Abbildung dargestellt.
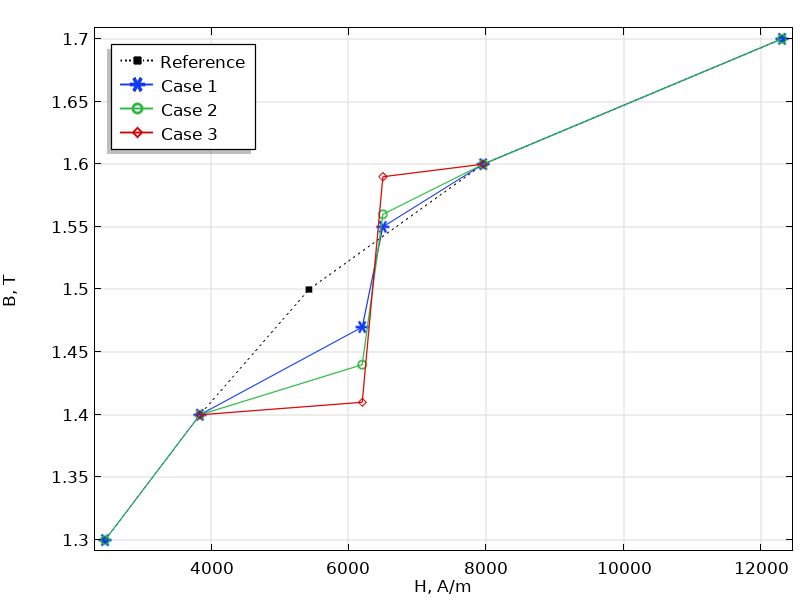
Die Darstellung von drei Gruppen von B-H-Kurven mit der Referenz der eingebauten B-H-Kurve. Beachten Sie, dass die Darstellung nur den Teil der Kurve zeigt, in dem die Unterschiede auftreten.
| Case |
B-H-Kurvendaten
H (A/m), B (T) |
Berechnungszeit |
|---|---|---|
| 1 |
… 3841.67, 1.4 6200, 1.47 6500, 1.55 7957.75, 1.6 … |
1 Minute, 17 Sekunden |
| 2 |
… 3841.67, 1.4 6200, 1.44 6500, 1.56 7957.75, 1.6 … |
1 Minute, 45 Sekunden |
| 3 |
… 3841.67, 1.4 6200, 1.42 6500, 1.58 7957.75, 1.6 … |
Nonlinear solver did not converge. Maximum number of Newton iterations reached. Time: 0.029466491699218753 seconds. Last time step is not converged. |
B-H-Kurvendaten und Berechnungszeiten für die drei Fälle.
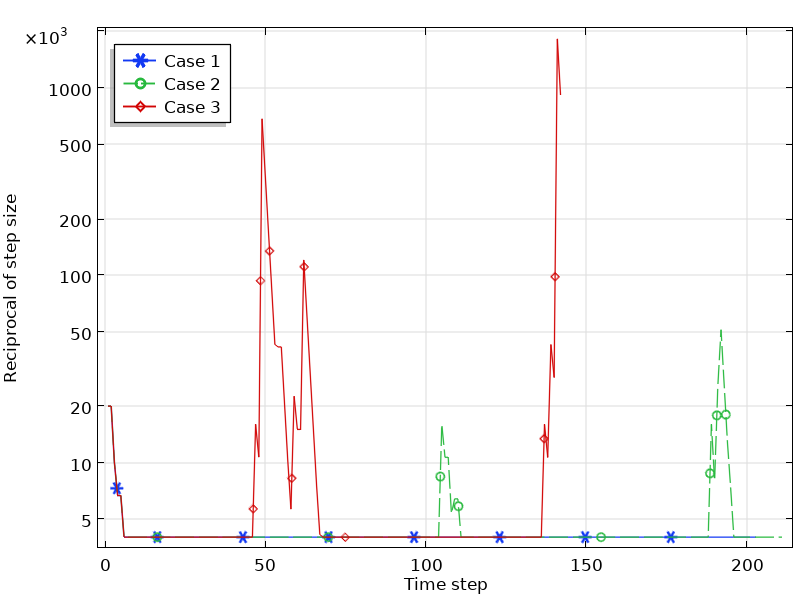
Das Konvergenzdiagramm der Simulationen für die drei Fälle.
Wie aus diesen Abbildungen ersichtlich ist, hat die Glätte der B-H-Kurve einen erheblichen Einfluss auf die Simulationsergebnisse. In Fall 1, in dem die Daten der B-H-Kurve geringfügig von der Referenz abweichen, läuft die Simulation reibungslos. Für Fall 2, bei dem die Änderung der B-H-Kurve bis zu einem gewissen Grad zunimmt, konvergiert die Simulation zwar immer noch, benötigt aber eine viel längere Simulationszeit. Wenn die Steigungsänderung weiter zunimmt, konvergiert die Simulation sogar nicht mehr (Fall 3).
Optimieren Sie die B-H-Kurve mit einem Mausklick
Seit Version 5.5 von COMSOL Multiphysics® ist die B-H Curve Checker App verfügbar. Diese Simulations-App kann zur Überprüfung und Optimierung der gemessenen B-H-Kurve verwendet werden. Die App kann die Kurvendaten in der gesättigten Region erzeugen, in der Messungen schwierig sind. Sie kann außerdem die unphysikalischen Peaks der Steigung der B-H-Kurve entfernen, die zu numerischen Instabilitäten führen könnten.
Die App bewertet die ursprüngliche B-H-Kurve nach zwei Gesichtspunkten:
- Ist die Extrapolation der Kurve aus physikalischer Sicht sinnvoll?
- Ist die Steigung der Kurve glatt?
Die Optimierungsalgorithmen beruhen hauptsächlich auf der simultanen exponentiellen Extrapolationsmethode bzw. der linearen Interpolationsmethode.
Die Anwendung benötigt als Eingabe die in einer Textdatei definierten Originaldaten der Kurve. Sobald die Kurve importiert ist, prüft die App, ob sie optimiert werden muss. Durch Klicken auf die Schaltfläche Optimize kann der Benutzer die optimierten Kurvendaten erzeugen, die in eine Textdatei exportiert werden können.
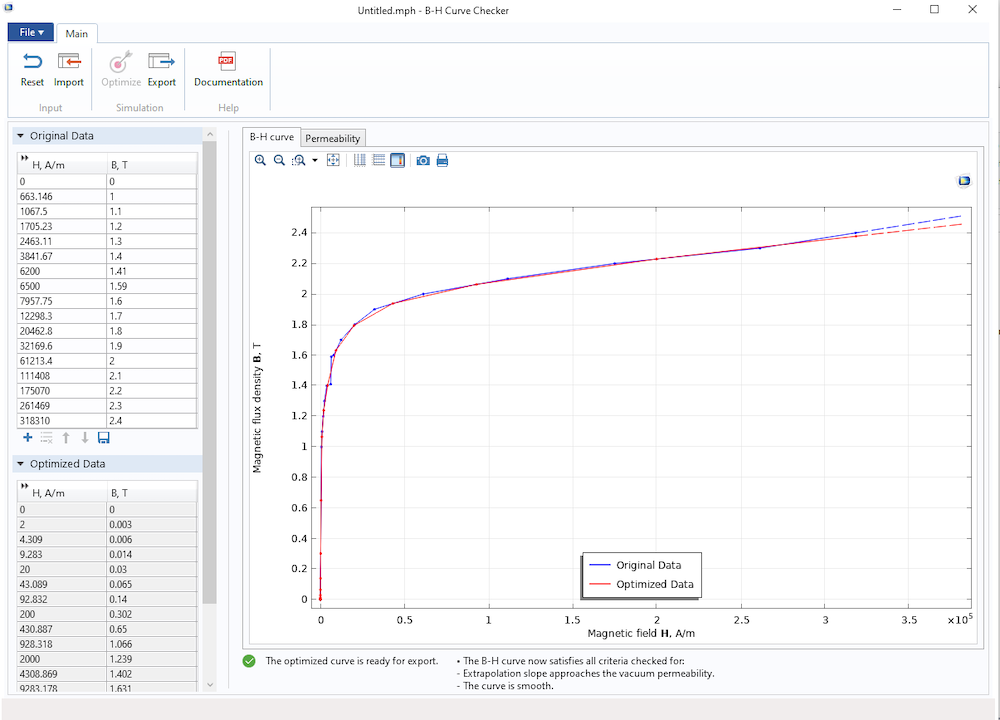
Die B-H Curve Checker App, mit den originalen und optimierten B-H-Kurven.
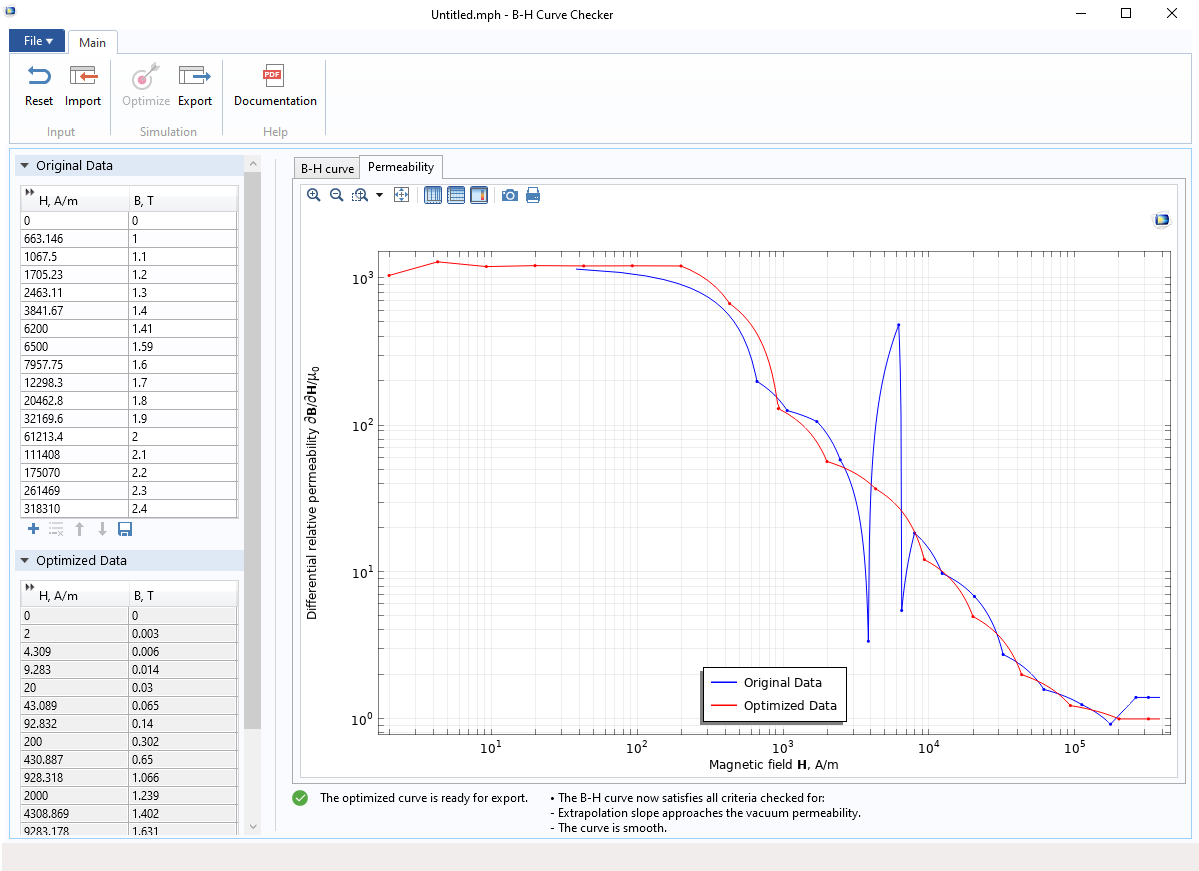
Die App “B-H Curve Checker”, die die differentielle relative Permeabilität der ursprünglichen und der optimierten B-H-Kurve zeigt.
Optimierte nichtlineare B-H-Kurven in der Materialbibliothek
Die B-H Curve Checker App wurde auf die vorimplementierten Materialien angewendet, von denen 35 für eine verbesserte Performance und Stabilität optimiert wurden. Die Liste der angepassten Materialien ist wie folgt:
- AC/DC Module material library
- Soft Iron (Without Losses), B-H curve and Effective B-H curve
- Soft Iron (With Losses), B-H curve and Effective B-H curve
- Nonlinear Permanent Magnet, B-H curve
- Nonlinear magnetic material library
- Silicon Steel NGO 35JN200
- Silicon Steel NGO 35PN210
- Silicon Steel NGO 35PN230
- Silicon Steel NGO 35PN250
- Silicon Steel NGO 50PN1300
- Silicon Steel NGO 50PN600
- Silicon Steel NGO 50PN700
- Silicon Steel NGO 50PN800
- Silicon Steel NGO M-22
- Silicon Steel GO 3%
- Silicon Steel GO 3413
- Silicon Steel GO 3423
- Silicon Steel GO Silectron 4 mil cross
- Silicon Steel GO Silectron 4 mil rolling
- Metglas Nano Finemet 50 Hz NoFieldAnnealed
- Cobalt Steel Vacoflux 50
- Nickel Steel 4750
- Nickel Steel Monimax Nonoriented
- Nickel Steel Mumetal 80% Ni
- Nickel Steel Square 50
- Nickel Steel Superperm 49
- Low Carbon Steel 50H470
- Low Carbon Steel Magnetite
- Low Carbon Steel Soft Iron
- Low Carbon Steel Vacofer S1 Pure Iron
- Alloy Powder Core Hiflux 125 mu
- Alloy Powder Core Hiflux 160mu
- Alloy Powder Core Koolmu 125 mu
- Alloy Powder Core Koolmu 40 mu
- Alloy Powder Core Koolmu 75 mu
- Alloy Powder Core Koolmu 90 mu
- Alloy Powder Core MPP 60 mu
Beachten Sie, dass Materialien, die einem Modell vor COMSOL Multiphysics® Version 5.5 hinzugefügt wurden, nicht betroffen sind, es sei denn, sie werden aus der Materialbibliothek neu hereingeladen.
Frequenzstudie für Weicheisenmaterialien
Die B-H-Kurve ist in der Regel nichtlinear und kann in stationären und zeitabhängigen Studien verwendet werden. Sie kann jedoch nicht direkt in Studien im Frequenzbereich verwendet werden. Für eine Lösung im Frequenzbereich benötigen Sie eine “periodengemittelte” B-H-Kurve, die ein nichtlineares Material bei der Grundfrequenz approximiert. Für weitere Informationen lesen Sie bitte unseren vorherigen Blogbeitrag: Magnetische Materialien im Frequenzbereich mit einer App modellieren.
Zusammenfassung
In diesem Blogbeitrag haben wir die weit verbreitete B-H-Kurve und ihre wichtigen Eigenschaften für die Modellierung von Weicheisenmaterialien vorgestellt. Außerdem haben wir anhand von Fallstudien gezeigt, wie die Einstellungen der Extrapolation und die Glätte der Kurve Ihre magnetischen Simulationen beeinflussen können.
Anschließend stellten wir die neue App vor, die in COMSOL Multiphysics® Version 5.5 veröffentlicht wurde, den B-H Curve Checker. Mit dieser App kann die gemessene B-H-Kurve nach dem Importieren der Kurve per Knopfdruck optimiert werden. Wir haben auch die Verbesserung aller B-H-Kurven in der Bibliothek der nichtlinearen magnetischen Materialien vorgestellt. Schließlich erwähnten wir, dass Sie eine weitere App, den Effective Nonlinear Magnetic Curves Calculator, verwenden können, um effektive B-H-Kurven für Studien im Frequenzbereich zu berechnen.
Verwandte Lektüre
Erfahren Sie mehr über die Modellierung von magnetischen Materialien im COMSOL Blog:
- Ferromagnetische Materialien in COMSOL Multiphysics® modellieren
- Transformator-Designs mit elektromagnetischer Simulation bewerten
- Magnetische Materialien im Frequenzbereich mit einer App modellieren
Reference
- D.K. Rao and V. Kuptsov, “Effective Use of Magnetization Data in the Design of Electric Machines With Overfluxed Regions”, IEEE Transactions on Magnetics, vol. 51, no. 7, pp. 1–9, 2015.




Kommentare (0)