Wie lange braucht ein Ingenieur, um eine Glühbirne anzuschalten?

Kürzlich gab es im Internet eine große Kontroverse über ein unterhaltsames Video, das versucht, einen großen Irrglauben über Elektrizität aufzuklären: dass die Energie in einem Stromkreis von Elektronen getragen wird. Obwohl das Video und viele der Antwortvideos sicherlich fesselnd sind, hat dieser Fall noch viel mehr zu bieten, und die Verwendung von COMSOL Multiphysics^® ist eine wunderbare Herangehensweise, der Theorie auf den Grund zu gehen. Lernen wir mehr!

Der Hintergrund der Kontroverse

Das Video, mit dem alles begann, heißt “The Big Misconception About Electricity“. Es stellt einen Schaltplan vor, welcher der unten stehenden Abbildung ähnelt. Eine ideale Batterie ist mit einem idealen Schalter verbunden, um eine ideale Stromquelle zu bilden. Diese Quelle ist an ein Paar widerstandsloser Drähte angeschlossen, die jeweils auf einer Länge von 300.000 Kilometern in entgegengesetzter Richtung verlaufen und schließlich zu einer Glühbirne führen, die sich einen Meter entfernt befindet. Obwohl nicht ausdrücklich erwähnt, wird angenommen, dass sich der gesamte Schaltkreis in einer Art leerem Universum befindet, frei von kosmischer Hintergrundstrahlung, welche von dieser Vorrichtung mit Sicherheit wahrgenommen werden würde.

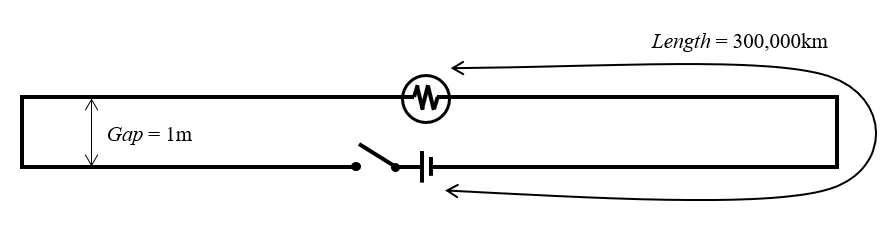
Abbildung des umstrittenen Schaltkreises.

Die Frage lautet: Wenn man den Schalter schließt, wie lange braucht ein Signal von der Stromquelle aus, um die Glühbirne zu erreichen? Die Antwort von 3,33 Nanosekunden (ns) ist richtig (Spalt/c \approx 3,33\text{ ns}, wobei c die Lichtgeschwindigkeit ist). Es gibt eine Reihe von Videos, die verschiedene Wege zeigen, diese Denkaufgabe zu verstehen:

• “Energy Doesn’t Flow Inside Wires – Is Veritasium Right – RSD Academy“
• “Electric Energy Doesn’t Flow in Wires – Follow-up No. 2 – RSD Academy“
• “I bought 1000 meters of wire to settle a physics debate“

Es wurde allerdings auch betont, dass wir einen Schwellenstrom definieren und uns fragen sollten, bei welcher Stromstärke sich die Glühbirne einschaltet. Das ist genau die Art von praktischen Problemen, die COMSOL Multiphysics^® in Angriff nehmen kann, also lassen Sie uns direkt einsteigen!

Ein numerisches Modell erstellen und die Ergebnisse verstehen

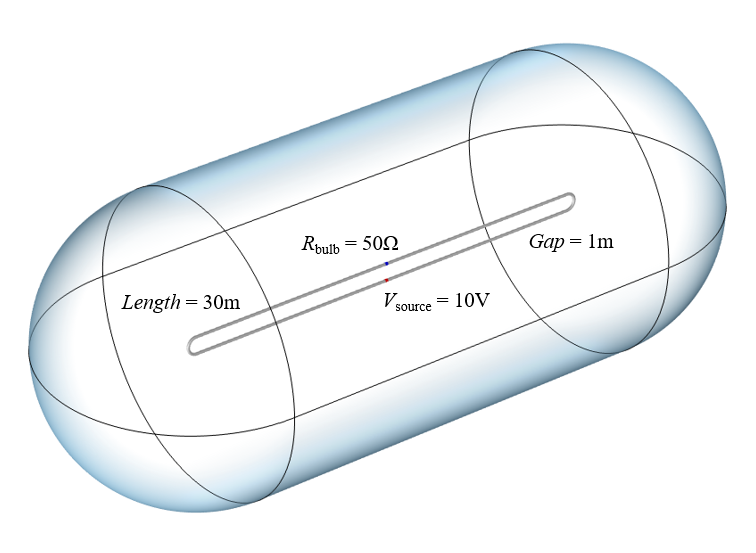
Eine Darstellung unseres Modells. Der Radius des Drahts beträgt 0,1 Meter und der Radius des Berechnungsgebiets 10 Meter.

Da wir die elektromagnetischen Felder in der Umgebung der Drähte berechnen werden, ist das Erstellen eines 300.000 Kilometer langen Modells wohl eher unpraktisch, aber wir können viel mit dem oben gezeigten, kleineren Modell herausfinden. Um die Stromquelle abzubilden, benutzen wir das Feature Lumped Port, das von der Zeit Null an eine gleichmäßige Spannung anlegt. Die Glühbirne wird als ein Lumped Element dargestellt, das einen Widerstand zur Lücke zwischen den beiden anderen Enden des Leiters darstellt. Die beiden 30 Meter langen Drähte werden durch die Randbedingung Perfect Electric Conductor modelliert. Die Annahme von perfekten Leitern ist plausibel, da solche Supraleiter bereits hergestellt werden. Das die Leiter umgebende Volumen wird als perfektes Vakuum behandelt und die Ränder dieses Volumens als offen in den leeren Raum hineinreichend. Sobald wir dieses Rechenmodell erstellt haben, können wir die Felder und Ströme auf den Leitungen berechnen und visualisieren.

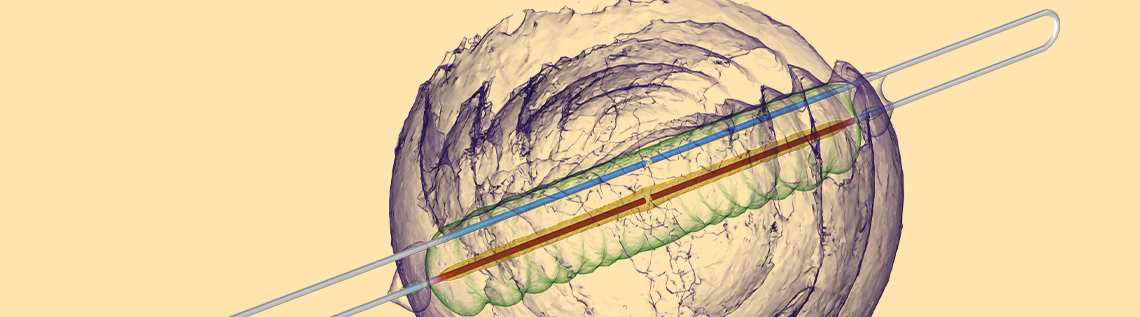
Die Ergebnisse zeigen die elektromagentische Energiedichte als semitransparente Isoflächen und den Strom entlang der Drähte. Ein Teil des Signals breitet sich mit Lichtgeschwindigkeit aus und induziert dabei Ströme am Draht jenseits des Spalts. Die Felder werden auch von den Drähten gelenkt und es gibt Strahlungsverluste. Nach etwas längerer Zeit wird das Verhalten durch die Induktivität und den Widerstand des Systems dominiert.

Die obige Animation zeigt die elektromagnetische Energiedichte in und um unseren Schaltkreis im zeitlichen Verlauf. Wir können beobachten, wie das Anfangssignal sich mit Lichtgeschwindigkeit ausbreitet, und sobald die zeitveränderlichen Felder die Drähte neben der Glühbirne erreichen, beginnen sie dort einen Strom zu induzieren. Die Felder werden hauptsächlich durch die Drähte gelenkt, obwohl es auch eine gewisse Abstrahlung gibt, besonders wenn die Felder an den Windungen reflektiert werden. Nach den ersten paar hundert Nanosekunden beginnen die Felder gleichförmiger zu werden. Wir können den Strom durch die Glühbirne auch graphisch gegen die Zeit auftragen und erörtern, was dessen Form über unser System aussagt.

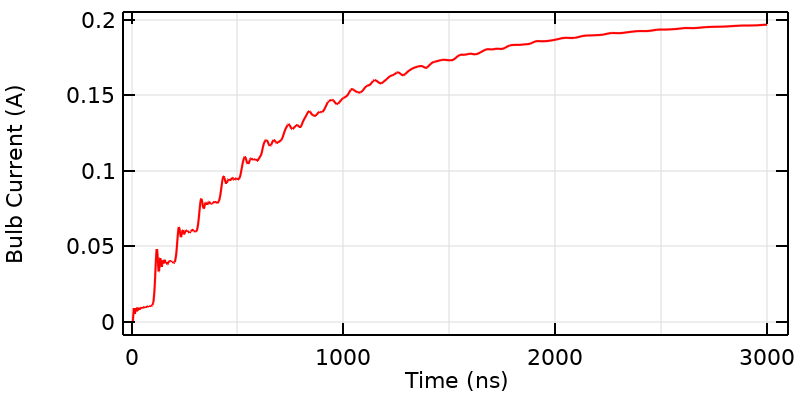
Der Glühbirnenstrom während einer längeren Zeitspanne, als das Signal normalerweise braucht, um sich über den Spalt hin auszubreiten, ähnlich des Verhaltens eines RL-Schaltkreises.

Die Gesamtform

Wenn wir uns den Gesamtverlauf der Kurve anschauen, steigt der Glühbirnenstrom anscheinend in Richtung eines Steady-State-Stroms. Das liegt daran, dass tatsächlich ein RL-Schaltkreis vorliegt. Wir können dann die Gesamtform der Kurve (nach 3,33 ns) mit dieser Gleichung beschreiben: I\left( t \right) = I_{DC}\left( 1 – exp(-t/\tau_{RL})\right), wobei die RL-Zeitkonstante \tau_{RL} = L_{wires}/R_{bulb} und die Induktivität L_{wires} mit einem Steady-State-Modell berechnet werden können. Die Gesamtinduktivität ist direkt proportional zur Länge der Drähte, sodass eine längere Schlaufe eine längere Anstiegszeit haben wird.

Wenn wir den Schwellenstrom beim Einschalten der Glühbirne als I_{DC}=V_{battery}/R_{bulb} definieren, dann wird der Strom (rein mathematisch gesehen) nur unendlich nahe an I_{DC} herankommen, und die Glühbirne wird sich tatsächlich nie einschalten. Nun, in Wirklichkeit wird die Glühbirne irgendwann angehen, denn was sie tatsächlich misst, ist die Geschwindigkeit und die Beschleunigung einer diskreten Anzahl von sich bewegenden Ladungen. Dennoch bedeutet ein Schwellenstrom, der sehr nahe am Gleichstrom liegt, dass die Glühbirne erst nach einer Zeit eingeschaltet wird, die viel größer als die RL-Zeitkonstante ist.

Die verschiedenen Plateaus

Wenn wir uns die Kurve in der Nähe der Startzeit genauer ansehen, erkennen wir, dass das Signal mehrere ausgeprägte Plateaus aufweist, die zu einer Art Treppenstufenform führen. Die charakteristische Zeit jedes dieser Plateaus beträgt 100 ns, da das angelegte Stufensignal den gesamten Draht durchläuft und an den Biegungen genau in der Mitte jedes Drahtes eine Reflexion erfährt. Die Höhe dieser Stufen hängt mit der kapazitiven und induktiven Kopplung über den Spalt hinweg zusammen.

Es ist möglich, dieses stufenförmige Verhalten mit einem Schaltungsmodell einer Übertragungsleitung zu charakterisieren. Beachten Sie, dass sich diese Plateaus mit der Zeit glätten; wir werden uns gleich damit befassen, woher diese Glättung kommt. Vorerst wollen wir uns mit der zweiten Möglichkeit befassen: Je nachdem, welchen Schwellenstrom wir angeben, könnte sich die Glühbirne bei einem ganzzahligen Vielfachen von 100 ns einschalten.

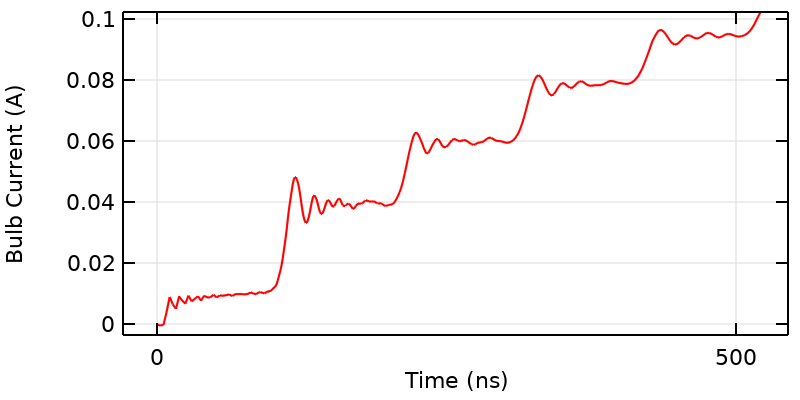
In der Nähe des Startzeitpunkts weist der Strom gegen die Zeit auch deutliche Plateaus auf, deren Periode der Zeit entspricht, die das Signal für die Ausbreitung über die gesamte Drahtlänge benötigt. Darüber hinaus gibt es Oszillationen, die durch die sprunghafte Veränderung des idealisierten Schalters und das Resonanzverhalten des Systems entstehen. Diese klingen mit der Zeit aufgrund der Verluste im System ab.

Die schnellen Oszillationen und ihr Abklingen

Wenn wir uns den Beginn jeder Stufe noch genauer anschauen, sehen wir, dass es deutlich erkennbare Wellen im Strom gibt, mit höheren Spitzen zu Beginn jeder Stufe, die allmählich abklingen. Das bedeutet, dass die Glühbirne bei der Wahl des richtigen Schwellenstroms erst flackert und dann leuchtet, was eine dritte Möglichkeit darstellt!

Diese Wellen sind auf die räumlich verteilte Kapazität und Induktivität des Systems zurückzuführen, die nicht nur zu einer, sondern zu einer unendlichen Anzahl von Resonanzen führen werden. Wir beobachten, dass die Resonanzmoden höherer Ordnung des Systems durch die Quelle angeregt werden. Es ist jedoch zu beachten, dass diese Schwingungen abzufallen scheinen. Dieses Abklingen und die Glättung des Signals sind auf Verluste zurückzuführen. Eine Verlustquelle ist der Widerstand unserer Glühbirne, die die im Akku gespeicherte Energie in Wärme und Licht umwandelt. Die zweite Verlustquelle ist auf die Abstrahlung von Energie von anderen Teilen unseres Schaltkreises zurückzuführen. Die korrekte Vorhersage dieses Verlustes erfordert genau die Art von dreidimensionalem Modell, das wir hier erstellen.

Der höherfrequente, kurzwellige Anteil wird schneller abgestrahlt als der niederfrequente Anteil. Man könnte auch sagen, dass höhere Resonanzen einen niedrigeren Qualitätsfaktor haben, oder dass die Drähte eine Art verlustbehafteter Tiefpassfilter sind.

Wir sollten uns auch fragen, wie der hochfrequente Anteil, der diese Resonanzen anregt, in das Modell kommt. Erinnern wir uns daran, dass wir beim Schließen des Schalters eine sprunghafte Änderung des angelegten elektrischen Potenzials einführen. Wir müssen uns fragen, welchen Frequenzgehalt diese Änderung hat. Diese Frage lässt sich durch eine Fourier-Transformation beantworten. Es stellt sich heraus, dass unser Eingangssignal einen unendlichen Frequenzgehalt hat. Der sehr hochfrequente Anteil hat einen geringen Betrag und strahlt schnell ab, aber er ist da. Es ist auch erwähnenswert, dass dieser Frequenzgehalt etwas über die Schaltung und ihren Aufbau aussagt. Wenn wir die Form der Biegung in der Mitte der Drähte ändern würden, würden wir andere reflektierte Signale erhalten.

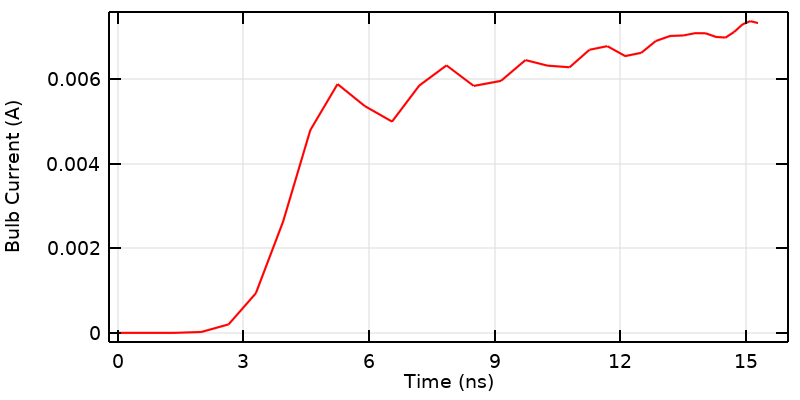
Betrachtet man die Ergebnisse in der Nähe der Startzeit, so fügt die Numerik als Folge unseres idealisierten Schalters eine kleine künstliche Streuung zum Modell hinzu. Dies könnte dadurch behoben werden, dass stattdessen das Eingangssignal langsam hochgefahren wird.

Die Lösung nahe der Startzeit

Ein letzter Bereich dieser Kurve verdient besondere Aufmerksamkeit. Ganz zu Beginn der Simulation ist das Signal zunächst gleich Null, wird aber vor 3,33 ns ungleich Null. Dies ist ein kleiner numerisches Artefakt, der entsteht, weil wir eine unphysikalische Situation modellieren: Einen Schalter, der sich sofort einschaltet. Ein solcher Schalter ist physikalisch unmöglich: Selbst die schnellsten bekannten physikalischen Prozesse haben Anstiegszeiten in der Größenordnung von einer Attosekunde. Wenn wir uns um diesen Teil der Ergebnisse sorgen würden, könnten wir unsere Stufenänderung durch ein transientes Signal ersetzen, das eine realistische Anstiegszeit hat. Außerdem müssten wir unser numerisches Modell mit einer feinen Zeitschrittweite und einer feinen räumlichen Diskretisierung lösen (was sehr lange dauern kann), um die Kurve glatter zu machen.

Eine andere Möglichkeit, diesen letzten Punkt zu betrachten, besteht darin, dass die zugrunde liegenden numerischen Methoden die Dispersion, die wir vergessen haben einzubeziehen, wieder hinzufügen. Dies ist eine Angelegenheit für Experten, die sich mit der numerischen Analyse beschäftigen, und wir können mit Sicherheit sagen, dass sich Informationen in der Realität nicht schneller als mit Lichtgeschwindigkeit fortbewegen.

Was ist schlussendlich die Antwort auf die Kontroverse?

Kurz gesagt, es gibt keine Kontroverse. Die korrekte Aussage des Originalvideos ist, dass es bei der betrachteten Schaltung 3,33 ns dauert, bis sich ein Signal von der Quelle zur Glühbirne ausbreitet.

Vollständiger ist es zu sagen, dass die Antwortkurve folgendes zeigt:

1. Eine Verzögerung, die sich aus der Zeit ergibt, die die elektromagnetischen Felder benötigen, um sich durch den Raum zwischen der Quelle und der Glühbirne auszubreiten, und nach der ein gewisser Strom induziert wird.
2. Eine RL-Schaltung, da es sich im Wesentlichen um eine sehr große Induktionsschleife aus Draht in Reihe mit einem Widerstand handelt.
3. Stufenförmige Plateaus, die als Folge der Signalreflexion an der scharfen Biegung an den Drahtmittelpunkten entstehen. Die Höhe dieser Stufen wird durch die induktive und kapazitive Kopplung zwischen den benachbarten parallelen Drähten bestimmt.
4. Schnelle Oszillationen, die als Folge der sprunghaften Änderung des Eingangssignals entstehen und die Resonanzen der Struktur anregen.
5. Dämpfung des Hochfrequenzanteils durch den Widerstand der Glühbirne und durch Strahlung.

Ein solches Modell zu erstellen und dessen Verhalten zu überprüfen, ist in COMSOL Multiphysics^® schnell und einfach zu bewerkstelligen. Hier sind einige andere mögliche Änderungen, die wir untersuchen könnten:

• Ändern des Radius der Drähte. Dadurch würde sich die Größe der kapazitiven Kopplung ändern und damit auch die Höhe der Stufen und die Periode der Wellen.
• Betrachten von Drähten mit endlicher Leitfähigkeit. Dies würde den Strom im Gleichgewichtszustand verringern, aber nur eine recht geringe Auswirkung auf das Signal unmittelbar nach 3,33 ns haben. Je nach Schwellenwert könnte sich die Glühbirne also bei 3,33 ns einschalten und einige Zeit später wieder ausschalten.
• Ändern der Ausrichtung der Drähte, so dass die beiden Drähte nahe beieinander bleiben und nicht mehr in entgegengesetzte Richtungen verlaufen. In diesem Fall kommt es zwar immer noch zu einer gewissen Überlagerung, aber die Drähte verhalten sich dann viel stärker wie eine Übertragungsleitung.

Wie könnte man diese Schaltung sonst noch verändern, um ein anderes Verhalten zu erreichen? Schreiben Sie dazu weiter unten Ihre Gedanken und Kommentare!

Zusatz für Anwender von COMSOL Multiphysics^®

Wenn Sie das Modell, das zur Erstellung der obigen Abbildungen verwendet wurde, herunterladen und andere Situationen ausprobieren möchten, können Sie dies über den unten stehenden Link tun. Das Modell wurde mit dem RF Module erstellt. Darüber hinaus haben wir eine Reihe weiterer Ressourcen, die für diese Art der Modellierung nützlich sind:

• Um ein paar fundamentale Konzepte über Spannung und Erdung im Fall von Gleichstrom zu verstehen, siehe “Existieren Spannung und Erdung?“
• Um mehr über die Übertragungsleitungssicht auf dieses System zu lernen, lesen Sie “Spannung und Erdung während des Modellierens von wellenartigen EM-Feldern“
• Um die Anregung über Lumped Port und Lumped Element zu verstehen, siehe “Modellieren von TEM- und Quasi-TEM-Übertragungsleitungen“
• Um zu verstehen, warum das Signal in diesem Beispiel vor t = 3,33 ns ungleich Null zu sein scheint, hilft es, die Finite-Elemente-Methode zu verstehen, welche das Problem räumlich und zeitlich diskretisiert.
• Um zu erfahren, wie Sie den Schalter realistischer darstellen, sehen Sie sich diesen Knowledge-Base-Eintrag an.
• Um eine ähnliche Modellierungstechnik bei einer realistischeren Vorrichtung zu sehen, sehen Sie sich unser Beispielmodell zu Time-Domain Reflectometry an.
• Um zu verstehen, wie der Skin-Effekt wegen endlicher Leitfähigkeit ins Spiel kommt, und wie Sie ihr Modell daran anpassen müssen, siehe “Modellieren von Materialien bei elektromagnetischen Wellen“.
• Um das Verhalten einer parallelen Übertragungsleitung vorherzusagen, siehe diesen Application-Gallerie-Eintrag.
• Wenn Sie sich unwohl mit der Annahme eines unendlichen und rauschfreien Universums fühlen, können sie stattdessen das System in einer Absorberkammer modellieren. Erfahren Sie mehr über dieses Modell in folgendem Application-Gallerie-Eintrag.
• Wenn Sie sich fragen, welchen Effekt ein ungleichförmiger Kabelradius in einer Übertragungsleitung hat, lesen Sie “Berechnung der Impedanz eines Hohlleiters“.
• Wenn Sie sich fragen, warum unser Modell so eine große Umgebung um den Draht herum mit einbezieht, siehe “Benutzung von Perfectly Matched Layers und Scattering-Randbedingungen bei elektromagnetischen Wellen“.
• Falls Sie bemerkt haben, dass alle Felder in diesem Modell symmetrisch zur Mitte sind, und falls Sie denken, dadurch das Modell vereinfachen zu können, haben Sie Recht. Um mehr zu erfahren, lesen Sie “Symmetrien ausnutzen, um magnetische Felder einfach zu modellieren“.
• Zum Schluss: Falls Sie Interesse an meiner Lieblingsdenkaufgabe in Elektromagnetik haben, schauen Sie auf “Berechnung der Induktivität eines geraden Kabels“.

Probieren Sie es selbst aus