
Bei Strömungssimulationen ist es oft wichtig, die Kräfte zu bewerten, die das Fluid auf den Körper ausübt – zum Beispiel die Auftriebs- und Widerstandskräfte auf eine Tragfläche oder ein Auto. Ingenieure können diese Körperkräfte nutzen, um die Effizienz und aerodynamische Leistung von Konstruktionen zu quantifizieren. Heute werden wir verschiedene Möglichkeiten zur Berechnung von Auftrieb und Strömungswiderstand in COMSOL Multiphysics® diskutieren.
Definitionen für Auftrieb und Strömungswiderstand
Wenn ein Fluid an einem Körper vorbeiströmt, übt die Strömung eine Kraft auf die Oberfläche aus. Wie in der Abbildung unten dargestellt, wird die Kraftkomponente, die senkrecht zur Strömungsrichtung steht, Auftrieb genannt. Die Kraftkomponente, die parallel zur Strömungsrichtung verläuft, wird Strömungswiderstand oder Luftwiderstand genannt. Der Einfachheit halber nehmen wir an, dass die Strömungsrichtung mit dem Koordinatensystem des Modells übereinstimmt. Später werden wir Ihnen zeigen, wie Sie die Auftriebs- und Widerstandskräfte in einer Richtung berechnen können, die nicht mit dem Koordinatensystem des Modells übereinstimmt.
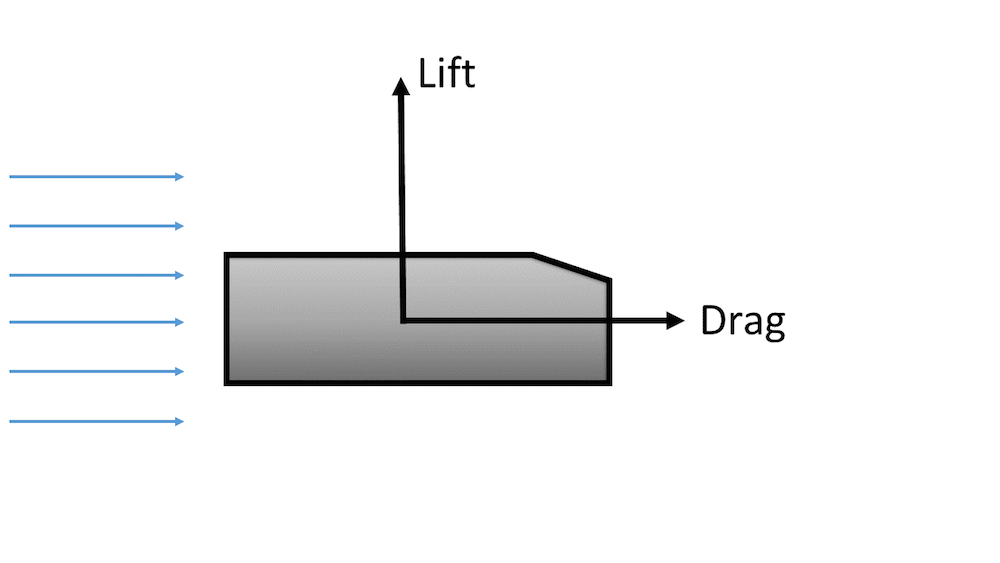
Schematische Darstellung von Auftriebs- und Strömungswiderstandskomponenten für ein Fluid, das entlang eines Objekts strömt.
Es gibt zwei verschiedene Faktoren, die zu den Auftriebs- und Widerstandskräften beitragen – die Druckkraft und die viskose Kraft. Die Druckkraft, die oft auch als Gradientkraft oder Druckgradientkraft bezeichnet wird, ist die Kraft, die durch den Druckunterschied auf der Oberfläche entsteht. Die viskose Kraft ist die durch Reibung verursachte Kraft, die in der entgegengesetzten Richtung der Strömung wirkt. Die Größenordnungen der Druckkraft und der viskosen Kraft können je nach Art der Strömung erheblich variieren. Die Strömung um ein sich bewegendes Auto wird zum Beispiel oft von der Druckkraft dominiert.
Auftrieb und Strömungswiderstand mithilfe der Gesamtspannung berechnen
COMSOL Multiphysics® bietet vollständigen Zugriff auf alle internen Variablen und macht die Berechnung von Oberflächenkräften durch Integration auf einem Rand sehr einfach. Hier zeigen wir Ihnen, wie Sie die Widerstandskräfte an einem Ahmed-Körper berechnen. Sie können dieses Modell aus unserer Application Gallery herunterladen.

Simulation der Luftströmung über einen Ahmed-Körper. Das Oberflächendiagramm zeigt die Druckverteilung, und die Stromlinien sind nach der Größe der Geschwindigkeit gefärbt. Die Pfeilfläche hinter dem Ahmed-Körper zeigt die Zirkulation in der Kielwasserzone.
Je nach physikalischen Gegebenheiten gibt es verschiedene Möglichkeiten, den Strömungswiderstand zu berechnen. Der einfachste Weg ist die Integration der Gesamtspannung – die Anteile der Druckkraft und der viskosen Kraft enthält – in jede Richtung. Dazu müssen wir zunächst einen Oberflächenintegrationsoperator unter dem Knoten Derived Values definieren, wie unten dargestellt.
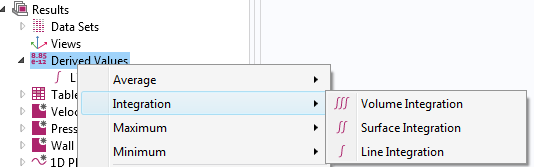
TIPP: Alternativ können Sie auch eine Randsonde (boundary probe) oder einen Integrationsoperator in der Komponentenkopplung verwenden, um eine solche Integration zu definieren. Der Unterschied besteht darin, dass die in den Physik-Einstellungen definierten Operationen während der Simulation verwendet werden können – zum Beispiel die mit einer Randsonde berechnete Strömungswiderstandskraft als Ziel oder Beschränkung in einer Optimierungsstudie.
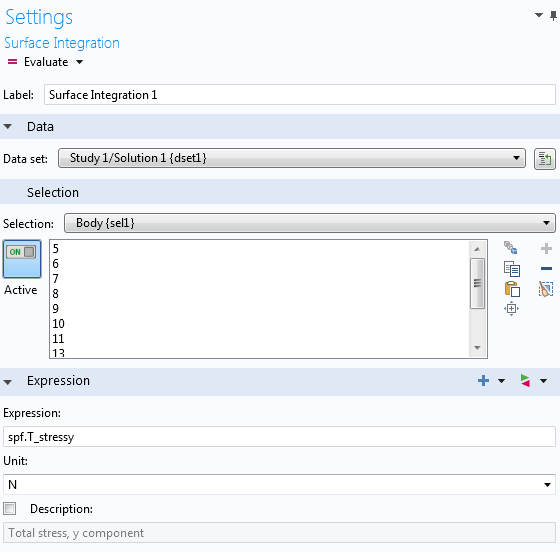
Als Nächstes können wir die Ränder auswählen, die integriert werden sollen. In diesem Beispiel haben wir alle Ränder des Körpers ausgewählt. Der Strömungswiderstand erfolgt in diesem Modell in y-Richtung. Wir können den Ausdruck spf.T_stressy eingeben, der der Gesamtspannung in y-Richtung entspricht.
Druckkraft und viskose Kräfte getrennt berechnen
Manchmal können Ingenieure einen besseren Einblick in Konstruktionen erhalten, wenn sie die Druckkraft und die viskose Kraft getrennt untersuchen. COMSOL Multiphysics® verfügt über eine vordefinierte Variable, spf.K_stressy, für die viskose Spannung in y-Richtung. Wir können die viskose Kraft ganz einfach durch Integration der viskosen Spannung berechnen.
Was ist mit der Druckkraft? Der Druck, der durch die Variable p bezeichnet wird, ist ein Skalar. Um in die Richtung des Strömungswiderstands zu projizieren, müssen wir den Druck mit der y-Komponente des Normalvektors auf der Oberfläche, spf.nymesh, multiplizieren. Daher können wir die Druckkraft durch Integration von spf.nymesh*p auf der Oberfläche berechnen.
In manchen speziellen Fällen der turbulenten Strömung, in der die Wall-Funktion verwendet wird, ist es genauer, die viskose Kraft mit Hilfe der Schubspannungsgeschwindigkeit, spf.u_tau zu berechnen. In COMSOL Multiphysics® verwenden die k-epsilon und k-omega Turbulenzmodelle die Wall-Funktion.
Mehr über Turbulenzmodelle in COMSOL Multiphysics® erfahren Sie in unserem Blog-Beitrag “Which Turbulence Model Should I Choose for My CFD Application?“.
Die lokale Schubspannung an der Wand erhalten wir durch:
Dementsprechend ist die lokale Schubspannung in y-Richtung:
wobei u^T die tangentiale Geschwindigkeit an der Wand ist. Außerdem können wir u^T als u_\tau*u^+ umschreiben, wobei u^+ die tangentiale dimensionslose Geschwindigkeit ist.
Ohne zu sehr ins Detail zu der Herleitung zu gehen, können wir die vorherigen Gleichungen in COMSOL-Variablen übersetzen. Wir können die lokale Wandschubspannung in der Richtung des Strömungswiderstands (der y-Richtung) mit dem folgenden Ausdruck integrieren: spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus. In diesem Ausdruck ist spf.rho die Dichte des Fluids, spf.u_tangy die Geschwindigkeit in y-Richtung an der Wand und spf.uPlus die tangentiale dimensionslose Geschwindigkeit.
Die folgende Tabelle fasst die Ausdrücke zusammen, die zur Berechnung der einzelnen Kräfte verwendet werden.
| Strömung ohne Wall-Funktion | Turbulente Strömung mit Wall-Funktion | |
|---|---|---|
| Druckkraft | spf.nymesh*p | spf.nymesh*p |
| Viskose Kraft | -spf.K_stressy | spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus |
| Gesamtkraft | -spf.T_stressy | spf.nymesh*p + spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus |
Hinweis: In diesem Beispiel liegt die Strömungswiderstandskraft in der y-Richtung. Möglicherweise müssen Sie die Projektionsrichtung je nach Ausrichtung Ihres Modells ändern.
Korrektur für den Anstellwinkel
Es kommt häufig vor, dass die Geometrie nicht perfekt auf die Strömungsrichtung ausgerichtet ist. Der Winkel zwischen der mittleren Bezugslinie der Geometrie und der einströmenden Strömung wird Anstellwinkel genannt (und oft mit dem griechischen Buchstaben \alpha bezeichnet). In der Luft- und Raumfahrttechnik wird der Anstellwinkel häufig verwendet, da er der Winkel zwischen der Sehnenlinie des Profils und der Richtung der freien Strömung ist. Die folgende Abbildung zeigt die Beziehung zwischen Auftrieb, Strömungswiderstand und Anstellwinkel bei einer Tragfläche.
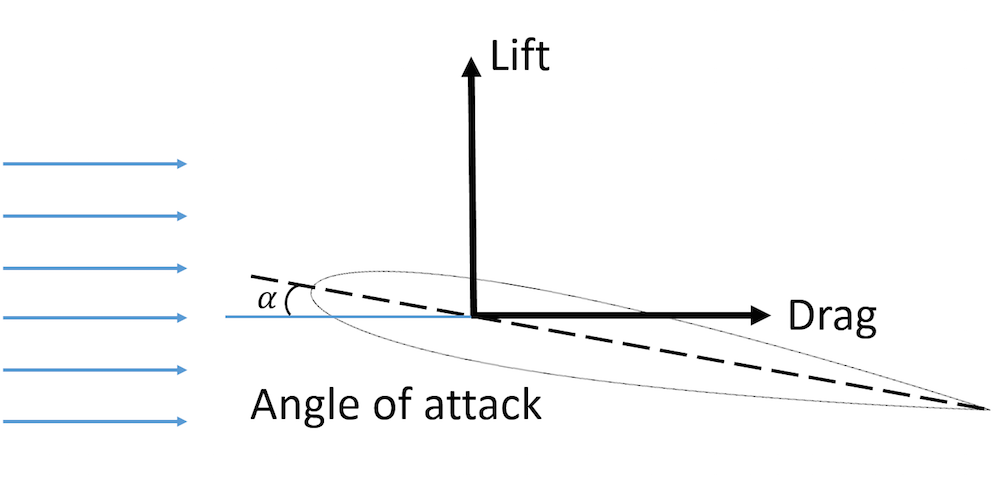
Schematische Darstellung von Auftrieb, Strömungswiderstand und Anstellwinkel an einer Tragfläche.
Mithilfe eines 2D-NACA-0012-Modells,werden wir Ihnen zeigen, wie Sie den Auftrieb mit einer Anstellwinkelkorrektur berechnen können. Dieses Modell steht zum Download in unserer Application Gallery bereit.
Es gibt zwei Möglichkeiten, den Anstellwinkel des Modells zu ändern. Wir können entweder die Geometrie selbst drehen oder die Geometrie beibehalten, aber die Strömungsrichtung am Einlass ändern. Hier werden wir den zweiten Ansatz verwenden. Es ist viel einfacher, das Geschwindigkeitsfeld an der Einlass-Randbedingung anzupassen, da wir das Modell nicht für jeden Anstellwinkel neu vernetzen müssen. Wie in der Abbildung unten zu sehen ist, ist die Tragfläche fixiert, während die Stromlinien die Strömung aufgrund der angepassten Richtung der Einlassgeschwindigkeit in einem Anstellwinkel zeigen.
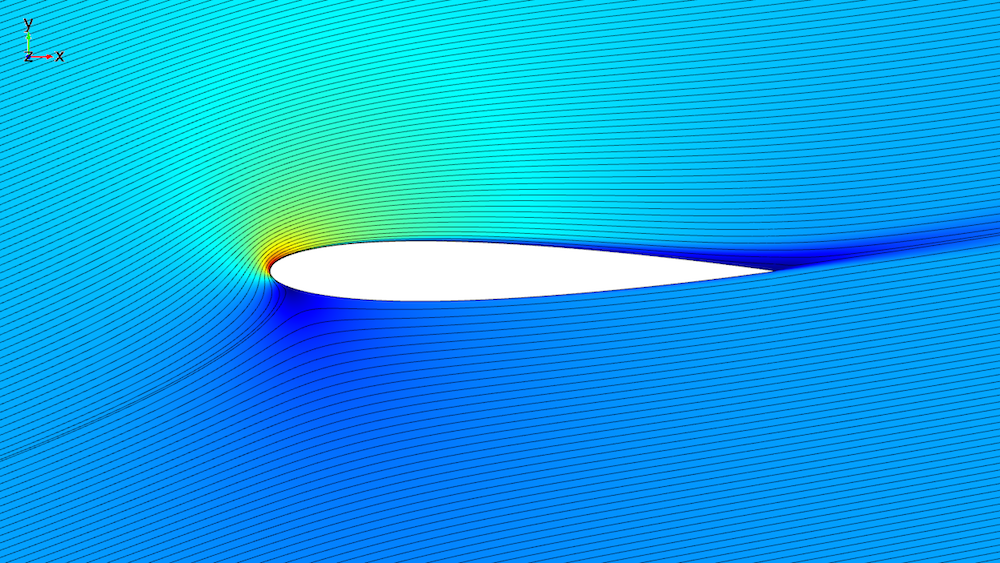
Simulation der Strömung an einer NACA-0012-Tragfläche mit einem Anstellwinkel von 14 Grad. Das Oberflächendiagramm zeigt die Geschwindigkeit zusammen mit den Stromlinien (in schwarz).
Dieses Beispiel verwendet das SST-Turbulenzmodell, das die Wall-Funktion nicht verwendet. Daher nutzen wir die Gesamtspannung, um den Auftrieb zu berechnen. Bei einem Anstellwinkel von Null ist der Auftrieb einfach -spf.T_stressy. Wenn der Anstellwinkel nicht Null ist, können wir die Kraft mit dem folgenden Ausdruck auf die Richtung des Auftriebs projizieren: spf.T_stressx*sin(alpha*pi/180)-spf.T_stressy*cos(alpha*pi/180). Dabei steht alpha für den Anstellwinkel in Grad.
Was ist mit Koeffizienten für Auftrieb und Strömungswiderstand?
Vielleicht interessieren Sie sich auch für die nicht dimensionierten Formen von Auftrieb und Strömungswiderstand – den Auftriebskoeffizienten und den Strömungswiderstandskoeffizienten. Es ist oft einfacher, die Koeffizienten anstelle der dimensionalen Kräfte zu verwenden, um experimentelle Daten zu validieren oder verschiedene Designs zu vergleichen. Der Auftriebskoeffizient in 2D ist definiert als:
Da wir den dimensionalen Auftrieb bereits berechnet haben, können wir den Auftrieb einfach durch den Dynamischen Druck und die Profilsehnenlänge normieren. Mit dem dimensionslosen Auftriebskoeffizienten können wir unsere Simulationsergebnisse mit experimentellen Daten vergleichen (Ref. 1).
Hinweis: In 3D wird der Auftriebskoeffizient nicht durch die Länge, sondern durch die Fläche dimensionslos: C_L = \frac{L}{\frac{1}{2} \rho u^2_\infty A}
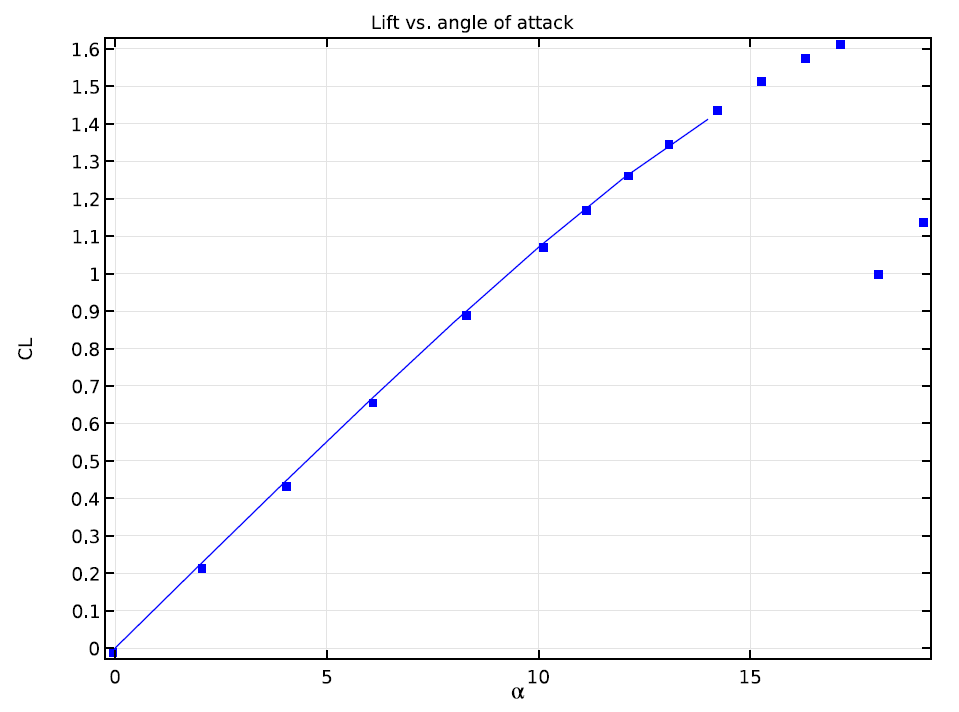
Grafik zum Vergleich von Simulationsergebnissen und experimentellen Daten des Auftriebskoeffizienten eines NACA-0012-Profils bei verschiedenen Anstellwinkeln.
Wie in der obigen Grafik zu sehen ist, gibt es innerhalb des Bereichs der in dieser Simulation verwendeten Anstellwinkelwerte keine erkennbare Diskrepanz zwischen den simulierten und den experimentellen Ergebnissen. Die experimentellen Ergebnisse gehen weiter in Richtung eines hohen Anstellwinkels, bei dem es zu einem Strömungsabriss kommt.
Abschließende Bemerkungen
In diesem Blog-Beitrag haben wir uns mit der Berechnung des Auftriebs und des Strömungswiderstands eines Ahmed-Körpers und einer NACA-0012-Tragfläche beschäftigt. Wir haben demonstriert, wie man die Druckkraft und die viskose Kraft berechnet, und haben dabei auch den Sonderfall untersucht, in dem eine Wall-Funktion in einem Turbulenzmodell verwendet wird.
Natürlich ist keiner der hier vorgestellten Ansätze auf diese speziellen Simulationen beschränkt. Sie können die Körperkräfte an beliebigen Rändern oder Oberflächen berechnen und so durch Multiphysik-Simulationen Einblicke in Konstruktionen gewinnen. Mit dem Optimization Module können Sie diese Analyse noch einen Schritt weiterführen und den Auftrieb oder Strömungswiderstand optimieren.
Referenzen
- C.L. Ladson, “Effects of Independent Variation of Mach and Reynolds Numbers on the Low-Speed Aerodynamic Characteristics of the NACA 0012 Airfoil Section,” NASA TM 4074, 1988.




Kommentare (0)