
Unter Ingenieuren, die sich mit Strömung beschäftigen, gab es schon immer eine Debatte über die Eignung von Finite-Elemente-Methoden für CFD. Einige Ingenieure sind der festen Überzeugung, dass die Finite-Volumen-Methode der Finite-Elemente-Methode überlegen ist. Gibt es eine wissenschaftliche Grundlage für diese Meinung? Nein, im Allgemeinen nicht. Verschiedene Methoden können für verschiedene Probleme geeignet sein. Wir werden uns ansehen, warum.
Wissenschaft, Technologie, und Tradition
Finite-Elemente-Methoden sind in der numerischen Analyse weit verbreitet, um numerische Methoden für die Strömung von Fluiden zu untersuchen. Es gibt eine große Anzahl von wissenschaftlichen Veröffentlichungen über CFD und Finite-Elemente-Methoden sowie neuere Arbeiten über nodale diskontinuierliche Galerkin-Methoden (DG-Methoden), d.h. Finite-Elemente-Methoden mit diskontinuierlichen Basisfunktionen.
Kommerzielle Pakete für CFD basieren traditionell auf Finite-Volumen-Methoden. Das liegt daran, dass im Grunde alle größeren kommerziellen Pakete für CFD die gleichen Vorfahren haben. In der Branche wird viel Arbeit und Technologie in diese Methoden investiert. Verschiedene Methoden wurden so implementiert, dass sie die Strömungen sowohl für strukturierte (z.B. Hexaeder; d.h. Ziegelsteine) als auch für unstrukturierte (z.B. Tetraeder) Netze effizient und genau berechnen und integrieren können.
Allerdings gibt es keine theoretische oder praktische Unterstützung für die Hypothese, dass Finite-Volumen-Methoden den Finite-Elemente-Methoden für Strömung überlegen sind. Erstens gibt es viele verschiedene Finite-Volumen-Methoden und Finite-Elemente-Methoden und einige dieser Methoden überschneiden sich. Zweitens hat die Implementierung einer Methode einen sehr großen Einfluss auf den praktischen Einsatz einer Software. Wir können sagen, dass Paket X für eine bestimmte Familie von Problemen besser geeignet zu sein scheint als Paket Y. Das liegt jedoch nicht daran, dass das eine FEM und das andere FVM verwendet. Lassen Sie uns dies im Folgenden erklären.
Finite Elemente Versus Finite Volumen: Was ist am Besten?
Mathematische Modelle und Numerische Modelle
Lassen Sie uns mit einem allgemeinen mathematischen Modell beginnen:
(1)
(2)
u = f{\text{ initial condition}} \hfill \\
Bu = g{\text{ boundary condition}} \hfill \\
\end{gathered} $
Hier bezeichnet P einen Differentialoperator, u die abhängige Variable (die Lösungsvariable), F eine Quelle, f eine Funktion, die die Anfangsbedingung beschreibt, B ein Operator, und g eine Funktion am Rand. Die Raumkoordinate \mathbf{x} repräsentiert in diesem Fall alle drei Richtungen (x, y und z).
Das mathematische Modell kann ein physikalisches Phänomen wie Strömung beschreiben. In diesem Fall kann das Modell die Erhaltung von Impuls und Masse in Raum und Zeit darstellen. Glücklicherweise verhält sich das mathematische Modell, das sich aus solchen Erhaltungssätzen ableitet und mit Anfangswerten und angemessenen Randbedingungen ergänzt wird, oft gut. Das bedeutet, dass es eine eindeutige Lösung gibt und dass sich die Lösung kontinuierlich auf die Daten für das Problem verhält, zum Beispiel auf die Anfangswerte, die Quellterme oder die Randbedingungen.
Trotz der Tatsache, dass ein Problem eine eindeutige und stabile Lösung hat, kann es schwierig oder fast unmöglich sein, eine solche Lösung analytisch zu finden. Das heißt, es kann schwierig sein, einen analytischen Ausdruck für die Lösung mit einfach zu berechnenden Operationen (+, -, x, ÷) zu finden. Stattdessen müssen wir ein numerisches Modell formulieren, das sich dem mathematischen Modell annähert. Die Gleichungen des numerischen Modells können dann mit einer numerischen Methode gelöst werden, die in einem Computerprogramm implementiert ist.
Finite-Elemente- und Finite-Volumen-Methoden sind numerische Methoden, die auf der Diskretisierung des Raums der Modellgleichungen basieren. Die zeitliche Diskretisierung erfolgt in der Regel mit einer Art von Zeitschrittschema für gewöhnliche Differentialgleichungen. Das oben definierte mathematische Modell ergibt das folgende numerische Modell:
(3)
(4)
{u_h} = {f_h}{\text{ initial condition}} \hfill \\
{B_h}{u_h} = {g_h}{\text{ boundary condition}} \hfill \\
\end{gathered} $
wobei h einen Diskretisierungsparameter bezeichnet, zum Beispiel das Netzelement oder die Zellengröße in einer Finite-Elemente- oder Finite-Volumen-Methode.
Beachten Sie, dass die Bausteine in einem Netz bei Finite-Elemente-Methoden als Elemente und bei Finite-Volumen-Methoden als Zellen bezeichnet werden.
Es gibt mehrere Fehlerquellen. Der Abschneidefehler, $\tau $, sagt uns, wie gut das numerische Modell das mathematische Modell approximiert:
(5)
Die Genauigkeitsordnung des numerischen Modells sagt uns, wie schnell der Abschneidefehler mit abnehmendem h abnimmt. Das bedeutet, dass die Differenz zwischen dem numerischen und dem mathematischen Modell umso geringer sein sollte, je kleiner das Element oder die Zellengröße ist. Ein numerisches Modell ist konsistent, wenn der Abschneidefehler mit h abnimmt.
Der Diskretisierungsfehler in den Lösungen wird als die Differenz zwischen der exakten Lösung und der numerischen Lösung der Modellgleichungen angegeben:
(6)
Man sagt, dass die numerische Methode konvergiert, wenn die numerische Lösung sich der exakten Lösung nähert, wenn h abnimmt:
(7)
Die Genauigkeitsordnung der Diskretisierung, p, sagt uns, wie schnell die numerische Lösung mit abnehmendem h gegen die exakte Lösung konvergiert.
(8)
Je größer p ist, desto schneller konvergiert die Näherung.
Gibt es also einen inhärenten Unterschied in der Genauigkeitsordnung von Finite-Elemente-Methoden und Finite-Volumen-Methoden? Indem wir die Ordnung der Basisfunktionen erhöhen, können wir mit Finite-Elemente-Methoden theoretisch jede beliebige Genauigkeitsordnung erreichen (in der Praxis gibt es andere Einschränkungen). Die gebräuchlichsten Finite-Elemente-Methoden haben eine Genauigkeit zweiter bis dritter Ordnung, und Finite-Volumen-Methoden haben eine Genauigkeit erster bis zweiter Ordnung.
Worin liegen die Ähnlichkeiten und worin die Unterschiede?
Schauen wir uns eine Flux-Balance-Gleichung an, die die Grundlage in mathematischen Modellen für Fluidströmung bildet:
(9)
In dieser Gleichung bezeichnet u die erhaltene physikalische Größe, wie z.B. Impuls oder Masse, und Gamma bezeichnet den Fluss dieser Größe, z.B. den Impuls, der pro Flächeneinheit und pro Zeiteinheit über eine Kontrolloberfläche fließt.
Finite-Elemente-Methoden beginnen mit der Formulierung einer Integralgleichung, bei der die Gleichungen mit Testfunktionen, \varphi, gewichtet werden, und die Mittelung durch Integration über den Modellbereich erfolgt:
(10)
Bevor wir jedoch fortfahren, lassen Sie uns das Divergenztheorem auf \[{\Gamma \varphi }\] anwenden. Dies ergibt den folgenden Ausdruck:
(11)
Dabei bezeichnet \Partial \Omega den Rand des Bereichs \Omega und \mathbf{n} den Normalenvektor zum Bereichsrand. Die Integration durch Teile der linken Seite in der obigen Gleichung ergibt:
(12)
was bedeutet, dass wir aus Gleichung 11 erhalten:
(13)
Damit haben wir jetzt die folgende Gleichung:
(14)
Wir können Gleichung 14 oben für den zweiten Term in Gleichung 10 verwenden. Dies geschieht, um die Randbedingungen des Flusses auf natürliche Weise in die Integralgleichungen einzubeziehen. Im weiteren Verlauf der numerischen Implementierung hat dies auch den Vorteil, dass der Flussvektor nicht differenzierbar sein muss. Daraus ergeben sich die Gleichungen, die als Ausgangspunkt für die Finite-Elemente-Methoden verwendet werden:
(15)
Dies ist die sogenannte schwache Formulierung. Der dritte Term auf der linken Seite integriert den Fluss von u, \Gamma, über den Rand des Bereichs, \partial \Omega.
Die schwache Formulierung hat nur dann etwas mit dem physikalischen Modell zu tun, wenn sie für eine große Variation von Testfunktionen \varphi gilt. Eine gängige Wahl ist die Verwendung von Polynomen, aber es können auch andere Arten von Funktionen sein. Ein Sonderfall ist der Fall einer konstanten Testfunktion; zum Beispiel \varphi = 1. Die letzte Gleichung oben, Gleichung 15, ergibt dann:
(16)
Diese Beziehung wird als Ausgangspunkt für Finite-Volumen-Methoden verwendet.
Bis jetzt gibt es keinen Unterschied zwischen der Finite-Elemente-Methode und der Finite-Volumen-Methode. Wie wir oben sehen, ist die Formulierung für Finite-Volumen-Methoden, Gleichung 16, nur ein Spezialfall der allgemeinen schwachen Formulierung, die bei Finite-Elemente-Methoden verwendet wird, Gleichung 15.
Der Unterschied liegt in der Diskretisierung von Gleichung 15 und Gleichung 16. Die Finite-Elemente-Methode erhält man, indem man eine endliche Anzahl von Testfunktionen \varphi = \varphi_h auswählt und verlangt, dass Gleichung 15 für alle von ihnen gilt. Die Methode der endlichen Volumina erhält man, indem man eine endliche Anzahl von Kontrollvolumina \Omega = \Omega_h auswählt und verlangt, dass Gleichung 16 für alle gilt. Wenn wir eine Triangulation als Grundlage für beide Methoden verwenden, zeigen die Abbildungen 1 und 2 mögliche diskretisierte Formen von Finite-Elemente- bzw. Finite-Volumen-Formulierungen.
Wenn wir uns die gängigsten Finite-Elemente-Methoden ansehen, dann sind die Testfunktionen nur in der Nähe von sogenannten Knoten ungleich Null (lokal unterstützte Funktion). Das bedeutet, dass die Integrale nur über die Elemente (hier: Dreiecke) in dieser Umgebung berechnet werden müssen. Siehe zum Beispiel den hervorgehobenen Bereichsknoten und die grau gefärbten Elemente in seiner Umgebung in Abbildung 1 unten. Der Beitrag der Randflüsse, der dritte Term auf der linken Seite in Gleichung 15, muss nur für Elemente berücksichtigt werden, die eine Fläche (3D) oder eine Kante (2D) an dem Rand haben, da sich die Beiträge zwischen den Elementen für kontinuierliche Basisfunktionen aufheben. Abbildung 1 unten zeigt, wie die Gleichung für interne Elemente in dem Bereich (weiß, grau und grün) und für Elemente, die eine Fläche (3D) oder eine Kante (2D) an der Grenze haben (hellblau), formuliert werden kann. Für den hervorgehobenen Knoten in dem Bereich in Abbildung 1 leisten nur die umliegenden grauen Elemente einen Beitrag zum Bereichsintegral (über \Omega). Für den hervorgehobenen Knoten am Rand liefern nur die beiden angrenzenden hellblauen Elemente einen Beitrag zum Integral über \partial \Omega, während sowohl diese beiden hellblauen Elemente als auch das hellgrüne Element Beiträge zum Bereichsintegral (über \Omega) liefern.
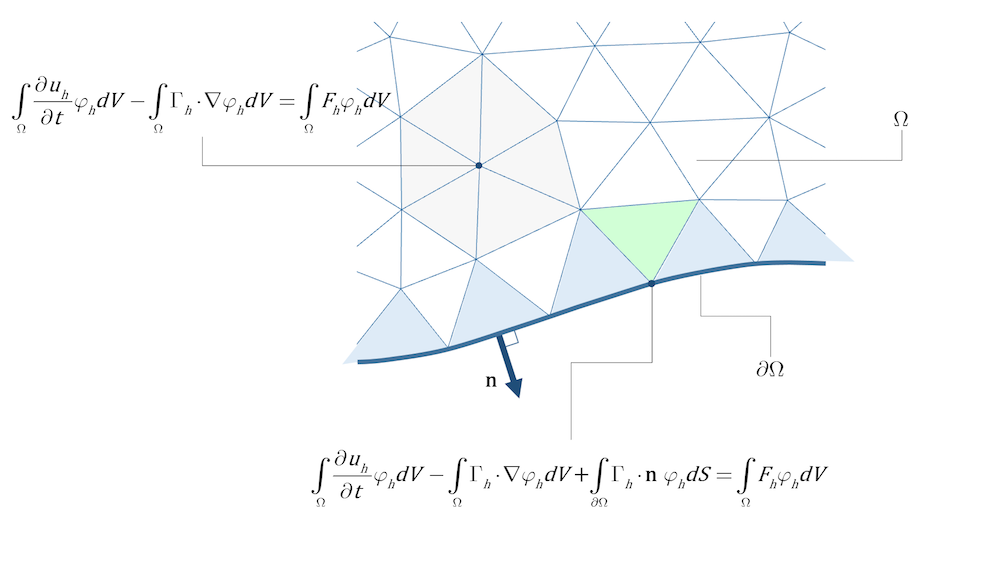
Abbildung 1. Der Bereichsbeitrag für interne Elemente (weiß und grau) und für Elemente, die eine Fläche (3D) oder Kante (2D) am Rand haben. Die Basisfunktion für den Knoten in der Mitte des grauen Sechsecks hat Unterstützung in allen umgebenden Elementen, d.h. in allen grauen Elementen. Die Basisfunktionen für die Knoten an den Grenzen haben Unterstützung in den hellblauen Elementen, aber auch in jedem Element, das einen Knoten an der Grenze hat, z.B. dem hellgrünen Element. Das Integral für den Fluss erhält nur Beiträge von den Elementen, die eine Kante an der Grenze haben (hellblaue Elemente).
Der Bereichsausdruck für den diskretisierten Fluss, \Gamma_h, ergibt sich aus den konstitutiven Beziehungen für den Fluss, z.B. der Konvektions-Diffusions-Gleichung (der Diffusionsterm in den Strömungsgleichungen ist der viskose Term für den Impulstransport). Die Randausdrücke für den Fluss in Gleichung 15 werden aus den Randbedingungen für das spezifische Modell gewonnen. Diese Ausdrücke sind dann als Beitrag für die Randelemente (hellblau) in Abbildung 1 oben enthalten.
Wenn wir stattdessen eine gängige Finite-Volumen-Methode, die zellzentrierte Methode, betrachten, wird jede Zelle (Dreieck) als ein individueller Bereich behandelt. Der Randterm für den Fluss, der zweite Term auf der linken Seite in Gleichung 16, wird für alle Zellen integriert, sowohl für interne Zellen als auch für Zellen, die eine Fläche (3D) oder eine Kante (2D) am Rand haben. Die konstitutive Beziehung für den Fluss wird für die Flächen oder Kanten des Bereichs verwendet, während die Randbedingungen für die Flächen oder Kanten an der Grenze verwendet werden; siehe Abbildung 2 unten.
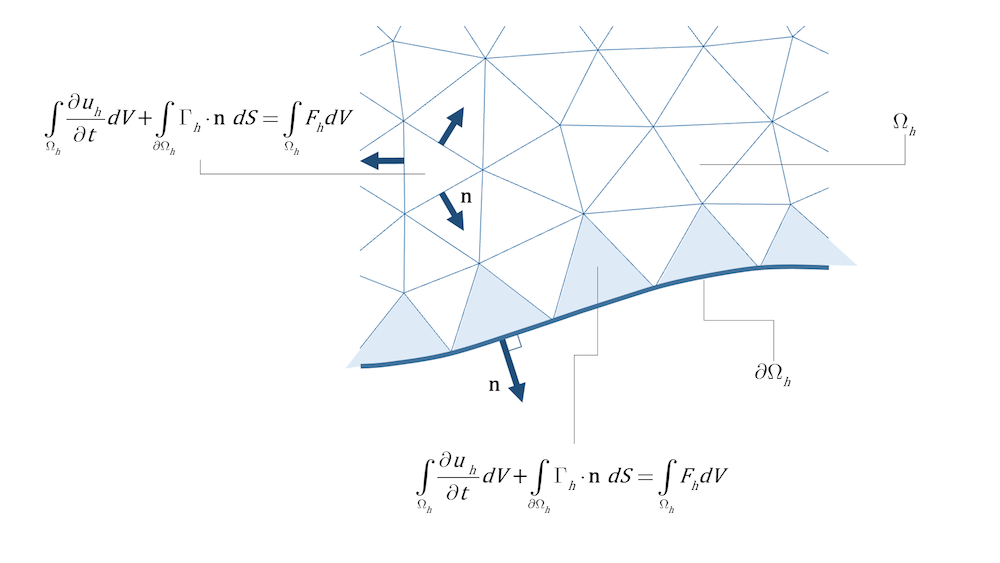
Abbildung 2. Der Fluss wird über alle Zellflächen (3D) oder Kanten (2D) integriert, sowohl für interne Zellen als auch für Zellen, die eine Fläche oder Kante an einem Rand haben.
Wie drücken wir also u und \Gamma in den beiden verschiedenen Methoden aus?
Bei Finite-Elemente-Methoden werden oft dieselben Basisfunktionen zur Approximation der Lösung verwendet wie die Testfunktionen. Solange die Approximation der Lösung einen höheren Polynomgrad als Null hat und die Ableitungen erster Ordnung approximiert werden können, muss nichts Besonderes getan werden, um einen durch Konvektion und Diffusion gegebenen Fluss zu behandeln. Der Flussvektor ist ebenfalls eine lokale Polynomialfunktion.
Bei Finite-Volumen-Diskretisierungen hingegen ist die Lösung am Rand nicht genau definiert. Die Methode definiert nur den Wert der Lösung für jede Zelle, der normalerweise als der Wert in der Mitte der Zelle interpretiert wird. Eine Finite-Volumen-Methode muss daher mit einer Art von Rekonstruktionsmethode ergänzt werden, um nützlich zu sein. In der Regel wird eine lokale Interpolationsmethode verwendet, bei der die Werte benachbarter Zellen berücksichtigt werden; siehe Abbildung 3 für ein Beispiel. Um eine Interpolation höherer Ordnung der Lösung und des Flusses zu erhalten, müssen mehr Zellwerte berücksichtigt werden. Das ist nicht nur kompliziert, sondern führt auch zu einer weniger lokalen Methode.
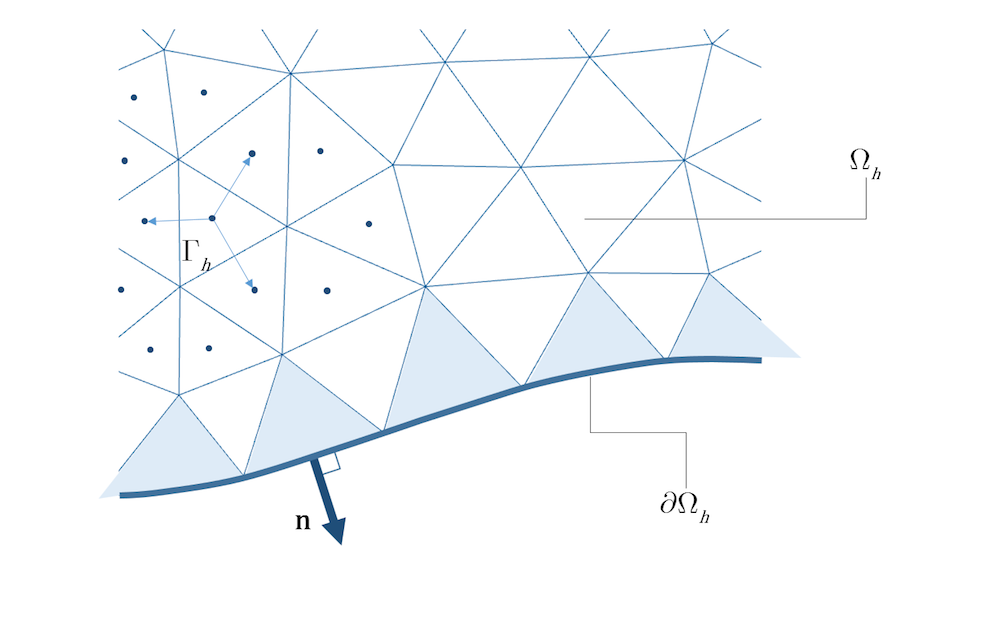
Abbildung 3. Bei einer zellzentrierten Finite-Volumen-Methode wird der Flussvektor durch Interpolation zwischen in der Zelle zentrierten Punkten konstruiert.
Je nach den in einer Finite-Elemente-Methode verwendeten Basisfunktionen und der Art der Konstruktion des Flusses, die in einer Finite-Volumen-Methode verwendet wird, können unterschiedliche Genauigkeiten erzielt werden. Ein grobes Netz mit einer Genauigkeitsmethode zweiter Ordnung kann eine genauere Lösung liefern als ein feineres Netz mit einer Genauigkeitsmethode erster Ordnung.
Lineare Testfunktionen und Basisfunktionen für die Finite-Elemente-Methode führen normalerweise zu Methoden, die eine Genauigkeit zweiter Ordnung aufweisen. Finite Elemente haben eine große Flexibilität, wenn es um die Diskretisierung geht. Die Verwendung quadratischer Basisfunktionen ist zum Beispiel recht einfach. Es ist auch keine Rekonstruktion oder Interpolation der Lösung erforderlich. Die Methode ist von Natur aus sehr symmetrisch, und Fluss-Randbedingungen an den Rändern können auf natürliche, direkte Weise festgelegt werden.
Ein Nachteil der FEM ist, dass es für kontinuierliche Test- und Basisfunktionen keine lokale Erhaltungseigenschaft gibt; nur die globale Erhaltung ist garantiert. Mit anderen Worten, nur der Nettofluss über die Bereichsränder ist garantiert im Gleichgewicht. Ein weiterer Nachteil ist, dass es keine Kontrolle über die lokalen Flüsse gibt, was bedeutet, dass eine Stabilisierung der Diskretisierung für konvektionsdominierte Strömungen nicht einfach ist. Stabilisieren bedeutet in diesem Fall, unphysikalische Oszillationen zu entfernen, die Artefakte der Diskretisierung sind. Sowohl die lokale Erhaltung als auch die Stabilisierung für die konvektionsdominierte Strömung können durch Modifizierung der schwachen Formulierung angegangen werden, entweder direkt oder indirekt, indem die Testfunktionen modifiziert werden. Diese Methoden können jedoch rechenintensiv sein.
Wie bereits erwähnt entsprechen Finite-Volumen-Methoden stückweise konstanten Finite-Elemente-Basisfunktionen, möglicherweise mit einem Interpolationsschema höherer Ordnung für die Flüsse. Dies führt zu Methoden, die erster oder zweiter Ordnung genau sind. Die lokale Formulierung für die Finite-Volumen-Methode führt zu lokaler Erhaltung, was eine attraktive Eigenschaft der Methode ist. Dies bedeutet, dass der Nettofluss für jede Zelle garantiert im Gleichgewicht ist. Sie führt auch zu natürlichen und direkten Wegen zur Stabilisierung der Diskretisierung für Strömungsprobleme, die von Konvektion dominiert werden. Die so genannte Upwind-Stabilisierung und andere Stabilisierungen werden auf natürliche Weise durch Modifizierung der Flüsse an den Zellgrenzen erreicht. Upwinding führt zu einer Nicht-Symmetrie der Diskretisierung in Richtung des konvektiven Flusses.
Die Finite-Elemente-Methode hat den Vorteil, dass sie Methoden für Basisfunktionen verschiedener Ordnungen formulieren kann. Höhere Ordnungen für die Basisfunktionen ergeben genauere Methoden höherer Ordnung, die den wichtigen Vorteil haben, dass sie die Genauigkeit für ein gegebenes Netz verbessern können. Die Finite-Volumen-Methode verwendet Basisfunktionen nullter Ordnung, kann aber stattdessen Interpolationsschemen höherer Ordnung für den Fluss verwenden, was ebenfalls zu einer verbesserten Genauigkeit führt. Wenn Sie Methoden höherer Ordnung verwenden, wird das resultierende System größer und die Lösungszeit erhöht sich bei gleichem Netz. Allerdings geht dies auch mit einer höheren Genauigkeit einher. Wenn wir also die Leistung vergleichen, müssen wir sie für eine bestimmte Genauigkeit vergleichen. Die Messung der CPU-Zeit und des Speichers, die erforderlich sind, um ein Strömungsproblem mit verschiedenen Methoden mit der gleichen Genauigkeit zu lösen, ist der richtige Weg, um die Leistung für diese verschiedenen Methoden zu vergleichen, nicht die Anzahl der Zellen oder Elemente.
Zukünftige Finite-Elemente-Methoden
Bei COMSOL arbeiten wir hauptsächlich mit Finite-Elemente-Methoden für CFD, da wir hier unsere Expertise haben. In den letzten 15 Jahren hat die Forschungsgemeinschaft große Fortschritte bei der Entwicklung von Finite-Elemente-Methoden mit diskontinuierlichen Test- und Basisfunktionen gemacht. Dabei handelt es sich um die in der Einleitung erwähnten DG-Methoden. Die Testfunktionen in diesen Methoden sind lokal für jedes Element und die schwachen Gleichungen gelten für jedes Element. Die lokale Erhaltung wird automatisch erreicht und Diskretisierungen höherer Ordnung sind einfach. Es ist auch keine Rekonstruktion der Lösung erforderlich, außer bei der Methode nullter Ordnung, die der Finite-Volumen-Methode entspricht. Darüber hinaus ist der lokale Fluss am Elementrand ein natürlicher Bestandteil der Formulierung, was bedeutet, dass die Stabilisierung einfach ist. Ein Nachteil der DG-Methoden ist die relativ große Anzahl von zusätzlichen Freiheitsgraden. Dies hat zur Untersuchung sogenannter hybrider DG-Methoden geführt, bei denen die Diskretisierung schlanker ist und weniger Freiheitsgrade ergibt.
Abschließende Gedanken zu FEM versus FVM
Wie wir hier gezeigt haben, haben sowohl die Finite-Volumen- als auch die Finite-Elemente-Methode ihre Vor- und Nachteile. Es gibt noch viele weitere Aspekte, die für eine effiziente Berechnung von Strömungsproblemen in großem Maßstab wichtig sind: effiziente und stabile Handhabung des Zeitschritts, effiziente Implementierung sowohl des impliziten als auch – in gewissem Maße – des expliziten Zeitschritts, Lösung großer linearer Gleichungssysteme und so weiter. Es gibt noch viel zu tun und es gibt noch viele Möglichkeiten, verschiedene Methoden und Technologien weiterzuentwickeln!
Wir bei COMSOL arbeiten ständig daran, die beste und neueste Technologie im Bereich der Finite-Elemente-Methoden anzubieten. Wir sind auch bestrebt, die besten Methoden im Allgemeinen zu entwickeln – nicht nur für Multiphysik, sondern auch für “einzelne” physikalische Anwendungen wie CFD.




Kommentare (0)