Auslegung von Heizkreisen mit multiphysikalischer Simulation

Heizschaltungen finden sich in Flugzeugen, elektronischen Anzeigetafeln, medizinischen Lagereinrichtungen und vielen anderen Geräten. Wie viele andere Heizelemente arbeiten sie mit Widerstandsheizung, einem multiphysikalischen Prozess, der elektrische Ströme, Wärmetransport und strukturelle Verformung beinhaltet. Um diese Phänomene und andere wichtige Designfaktoren zu berücksichtigen, können Ingenieure mit COMSOL Multiphysics^® virtuelle Prototypen von Heizschaltungen erstellen.

Erwärmung von Produkten mit Heizkreisen

Heizkreise können ein Produkt oder eine Flüssigkeit lokal erwärmen, eine nützliche Eigenschaft für viele industrielle Anwendungen. Sie werden häufig in Verbindung mit Temperaturfühlern verwendet und können in folgenden Bereichen eingesetzt werden

• Verhinderung von Vereisung und Beschlagen von Brillengläsern und Windschutzscheiben (z. B. in Autos und Flugzeugen)
• Schutz elektronischer Geräte im Freien (z. B. Anzeigetafeln) vor Feuchtigkeit und extremen Temperaturschwankungen
• Konstanthaltung der Temperatur von Medizinprodukten und Proben während der Prüfung und Lagerung
• Erwärmung von Klebstoffen und Flüssigkeiten in Fertigungsprozessen

Elektronische Anzeigetafel für eine Autobahn. Bild vom Oregon Department of Transportation. Lizenziert unter CC BY 2.0, via Flickr Creative Commons.

Diese Heizelemente funktionieren durch Widerstandsheizung, auch Joulesche Erwärmung genannt, die mehrere physikalische Phänomene involviert:

1. Wenn eine Spannung angelegt wird, beginnen elektrische Ströme durch den Stromkreis zu fließen
2. Diese Ströme erzeugen aufgrund des elektrischen Widerstandes des Materials des Stromkreises Wärme
3. Die steigende Temperatur führt zu einer Verformung des Bauteils

Die Verformung kann zwar manchmal nützlich sein (z. B. bei Thermoaktuatoren), sie kann aber auch ein Designproblem für Heizkreise darstellen. Diese Schaltkreise sind oft mit einem anderen, nicht leitenden Material verbunden, und eine zu starke Biegung kann den Klebstoff überlasten und dazu führen, dass sich die Widerstandsschicht ablöst – was wiederum dazu führen kann, dass die Schicht in Brand gerät. Designer müssen auch darauf achten, dass das Teil die verwendete Flüssigkeit oder das Produkt nicht überhitzt. Dies kann aufgrund der zahlreichen physikalischen Phänomene, die bei der Widerstandsheizung eine Rolle spielen, sowie der Vielzahl von Faktoren (wie die angelegte Spannung, die Geometrie, die verwendeten Materialien, die Umgebungsbedingungen usw.), die die Effektivität eines Heizkreises beeinflussen, eine Herausforderung darstellen.

Mit Hilfe der COMSOL^® Software können Ingenieure die Leistung von Heizkreisen unter Berücksichtigung verschiedener Phänomene und Auslegungsfaktoren bewerten und verbessern. Im nächsten Abschnitt sehen wir uns ein Beispiel an: ein multiphysikalisches Modell eines kleinen Heizkreises. Beachten Sie, dass zur Erstellung dieses Modells das Add-On Heat Transfer Module, Structural Mechanics Module und entweder das AC/DC Module oder das MEMS Module benötigt werden.

Modellierung der Multiphysik von Heizkreisen

Das Modell besteht aus zwei Teilen: einer Widerstandsschicht und einer Glasplatte. Die Widerstandsschicht besteht aus Nichrom, einem üblichen Material für Widerstandsheizelemente, und ist 10 µm dick und 5 mm breit. Wie in der Abbildung unten zu sehen ist, hat sie die Form einer Serpentine, deren Enden mit silbernen Kontaktpads versehen sind. Die Oberseite der Glasplatte (wo sich die Widerstandsschicht befindet) ist von Luft umgeben, während die Unterseite einer reaktiven Flüssigkeit ausgesetzt ist.

Nachdem die Geometrie festgelegt wurde, besteht der nächste Schritt darin, die Wärmeerzeugung und den Wärmetransport für eine angelegte Spannung (in diesem Fall 12 V) zu modellieren. Um die Wärmequelle zu bestimmen, die aus dem Stromfluss in der Widerstandsschicht resultiert, kann das Interface Electric Currents in Layered Shells verwendet werden. Dieses Interface berechnet die Stromerhaltung und eignet sich besonders für Schichten, die geometrisch sehr dünn, aber elektrisch sehr groß sind. In diesem Fall ist die geometrische Dicke der Schicht so gering, dass sie vollständig aus der Geometrie und dem Netz entfernt werden kann, was die Handhabung der Geometrie und des Netzes drastisch vereinfacht. Gleichzeitig ist eine Dicke von Null aus physikalischer Sicht keine geeignete Näherung. Der Grund dafür ist der große Unterschied in den Materialeigenschaften zwischen der Schicht und ihrer Umgebung. Das Interface Electric Currents in Layered Shells verwendet die entsprechende Dicke bei der Lösung der Gleichungen, auch wenn sie nicht explizit in der Geometrie enthalten ist.

Ein ähnlicher Ansatz wird für das Wärmetransportproblem verwendet. Das Modell nutzt die Vorteile der Thin Layer-Funktion im Heat Transfer in Solids-Interface und der Electromagnetic Heating-Multiphysik-Kopplung, die automatisch die Physik für die Simulation der Joule-Erwärmung kombiniert. In diesem Beispiel wird dann das thermische Problem in der Schicht mit der Platte gekoppelt und mit Hilfe von Wärmetransportkoeffizienten simuliert, wie die Wärme von der Platte auf die Flüssigkeit übertragen wird und wie die Wärme durch natürliche Konvektion an die Umgebungsluft abgegeben wird.

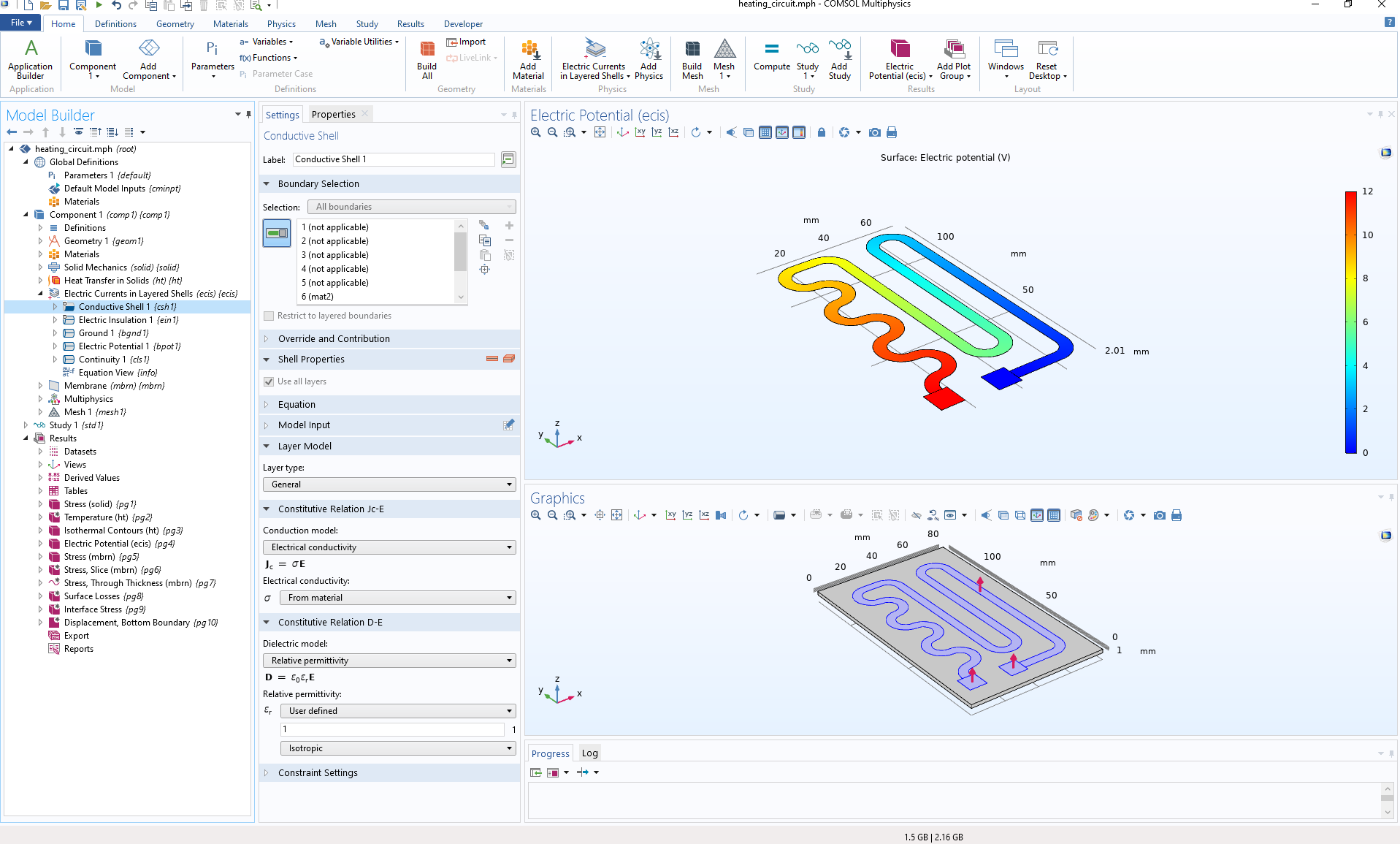
Screenshot, der die Modellierung der elektrisch erzeugten Wärme in der Widerstandsschicht zeigt.

Um die daraus resultierende Verformung (und mögliche Delamination) auf einfache Weise zu simulieren, können zwei stationäre strukturmechanische Analysen durchgeführt werden. Hierbei ist das Solid Mechanics Interface eine gute Wahl für die Glasplatte, während das Membrane Interface (besonders geeignet für dünne Strukturen) für die Widerstandsschicht verwendet wird.

Verifizierung der Simulationsergebnisse für das Heizelement

Wärmeerzeugung und -transport

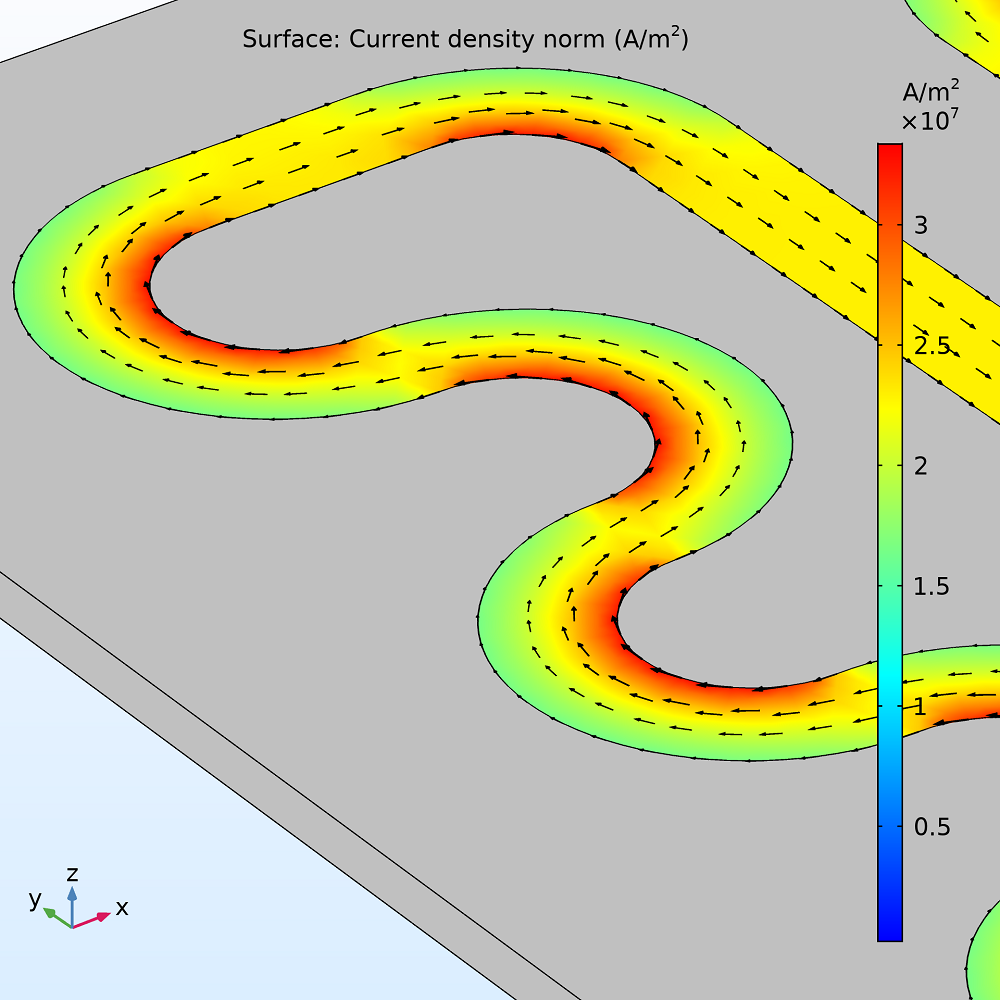
Die Lösung des Modells ermöglicht es, die in der Widerstandsschicht erzeugte Wärme sichtbar zu machen. Die stärkste Wärmequelle befindet sich dort, wo die Stromdichte am höchsten ist: in den inneren Kurvenbögen. Diese Stromkonzentration ist darauf zurückzuführen, dass der Potentialgradient umgekehrt proportional zum Abstand zwischen dem Masseanschluss und der Klemme ist. Da die inneren Kurvenbögen den kürzesten Weg darstellen, treten dort naturgemäß die höchsten Ströme auf. Integriert man über die Oberfläche der Widerstandsschicht, so erhält man die durch den elektrischen Widerstand erzeugte Gesamtwärme von ~13,8 W.

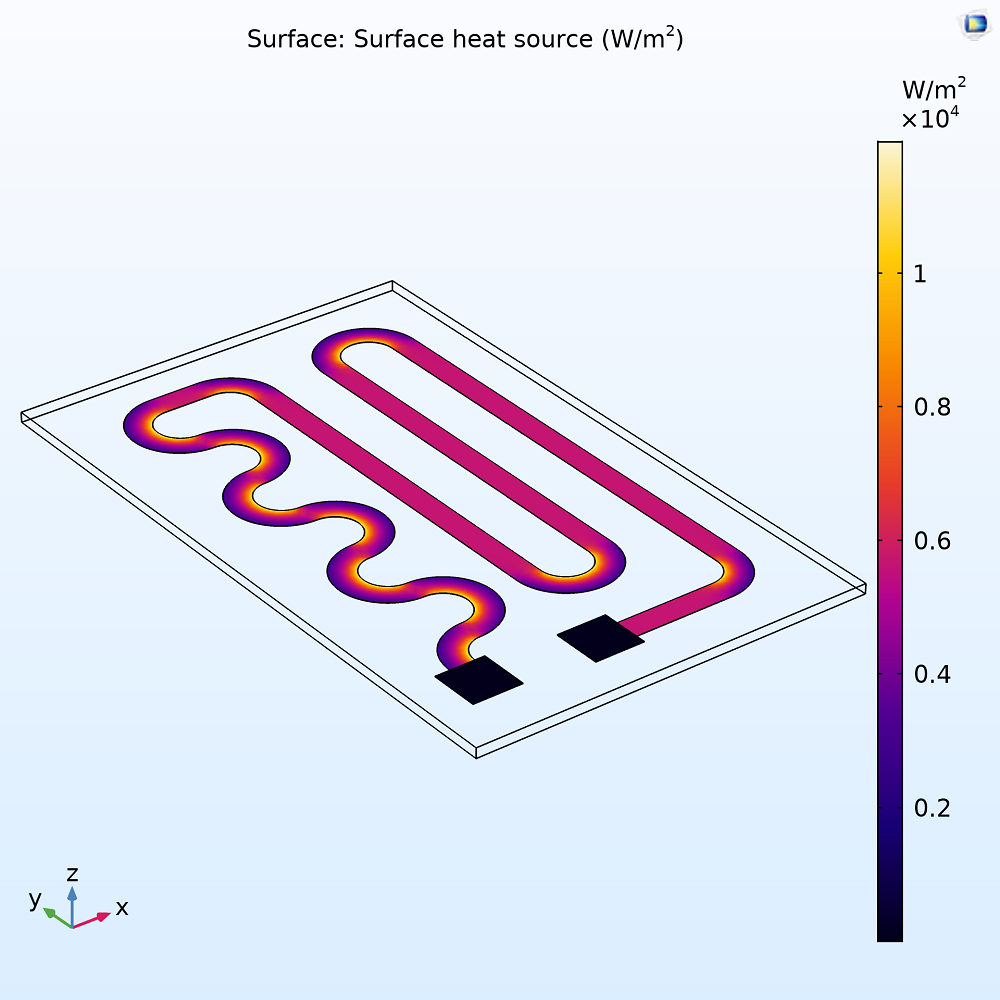
Stromdichte (links) und Wärmeerzeugung (rechts) in der Widerstandsschicht.

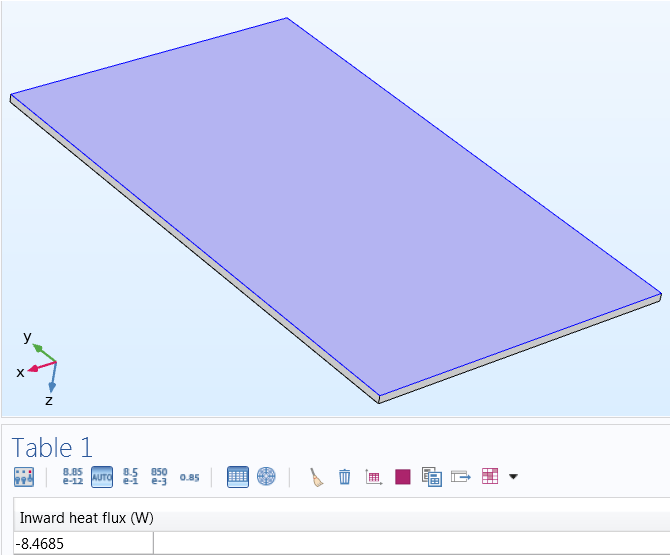
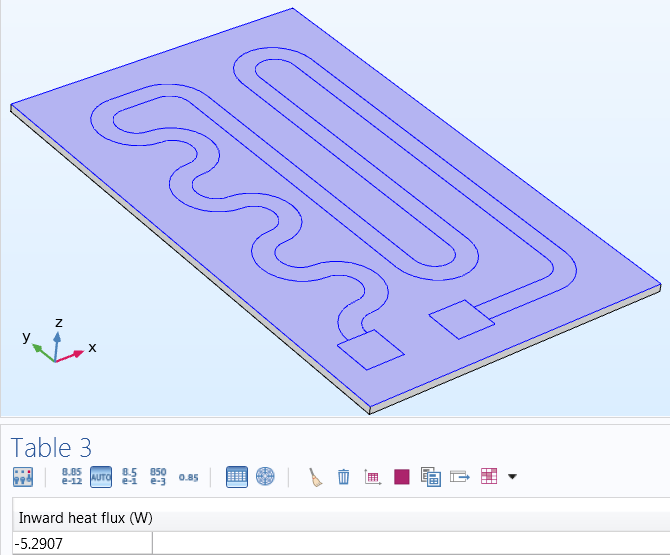
Um den Wirkungsgrad des Geräts zu bestimmen, kann man zunächst die elektrische Eingangsleistung sowie die Wärmeerzeugung und -abgabe bewerten. Hier ist die Eingangsleistung (gegeben durch V*I, in diesem Fall 12 Volt und 1,15 Ampere) gleich der gesamten erzeugten Wärme: 13,8 W. Wie unten gezeigt, tritt die höchste Temperatur in der Mitte des Stromkreises auf: 154,1°C. Durch Integration über die Fläche der Unterseite der Platte erhält man die an die Flüssigkeit abgegebene Wärmemenge: 8,5 W. Ebenso kann man die Wärmemenge berechnen, die an die Umgebungsluft abgegeben wird: 5,3 W. Dies zeigt nicht nur, dass die Konstruktion bei der Erwärmung der Flüssigkeit relativ effizient ist – 62 % der erzeugten Wärme werden übertragen -, sondern auch, dass die Energie erhalten bleibt, da die abgegebene Energie gleich der zugeführten Energie ist.

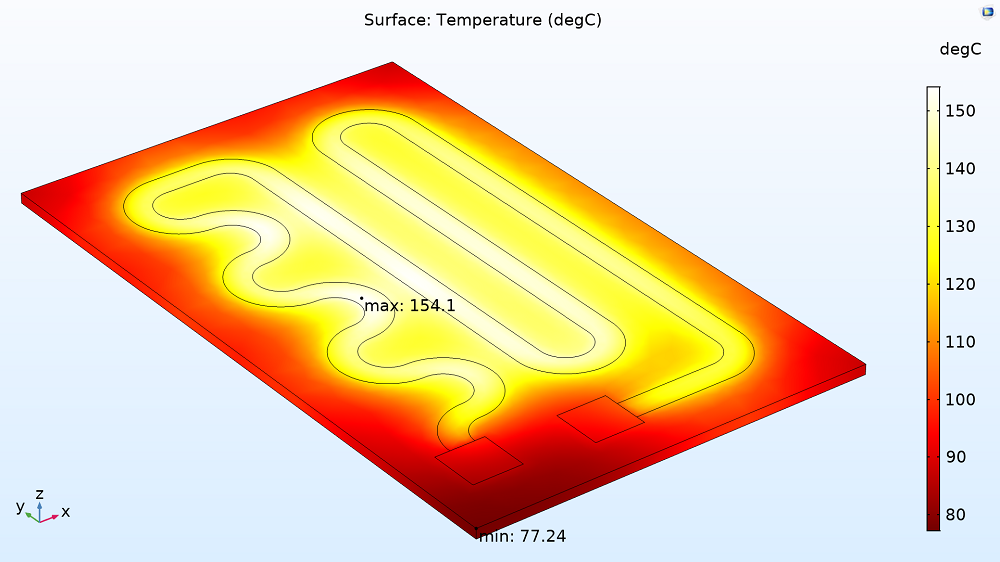
Temperaturverteilung in der Schicht und in der Platte, die zeigt, wo die höchsten (154,1 ºC oder 309,5 ºF) und niedrigsten (77,2 ºC oder 171 ºF) Temperaturen auftreten.

Wärme, die durch den unteren Teil (~8,5 W) und den oberen Teil (~5,3 W) des Heizkreises abgeführt wird.

Spannung, Deformation und Delamination

Die Vergleichsspannung kann verwendet werden, um festzustellen, ob ein Heizkreisdesign versagen wird. In diesem Modell verformen sich die Schicht und die Platte um ~50 μm und biegen sich zur Luft hin. Die Biegung belastet die Konstruktion, insbesondere an den inneren Ecken des Kreises, wo die Vergleichsspannung mit ~13 MPa ihren höchsten Punkt erreicht. Dies liegt jedoch weit unter der maximalen Streckspannung für Glas und Nickel-Chrom (250 bzw. 360 MPa), so dass beide intakt bleiben.

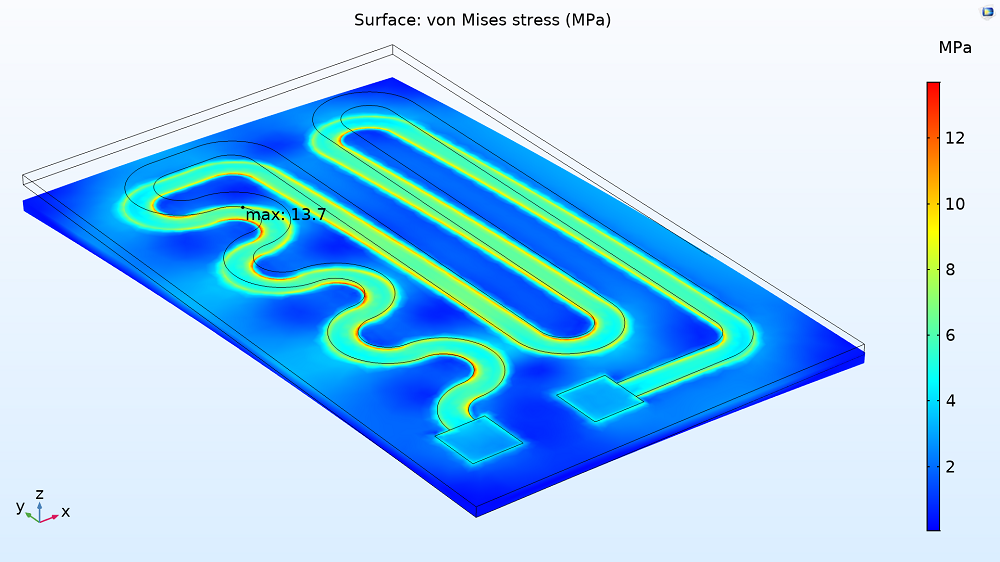
Die von-Mises-Spannung im Heizkreis.

Nun stellt sich die Frage, ob die beiden zusammen bleiben oder nicht. Um festzustellen, ob es zu einer Delamination kommt, kann man die Grenzflächenspannung zwischen der Nickel-Chrom-Schicht und der Glasplatte untersuchen. In diesem Fall ist die Spannung viel niedriger als die Fließspannung der Oberflächenhaftung (50 MPa), was darauf hindeutet, dass die beiden Elemente ohne Probleme zusammenbleiben.

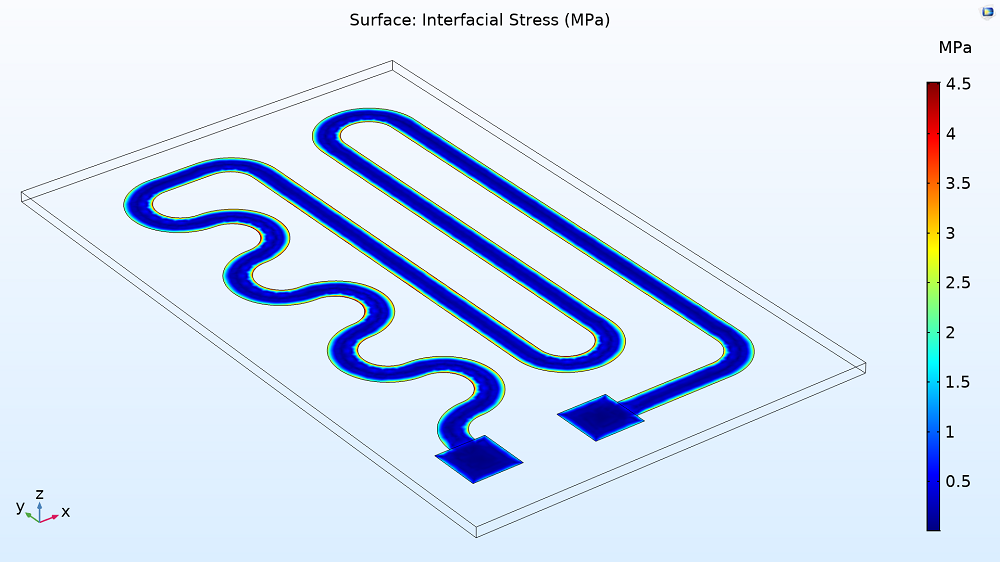Die Grenzflächenspannung im Heizkreis.

Wie dieses Beispiel zeigt, können Ingenieure die COMSOL^®-Software verwenden, um Heizkreise zu analysieren und dabei die zahlreichen beteiligten physikalischen Phänomene zu berücksichtigen. Die Ergebnisse können dann verwendet werden, um den Entwurf für eine bestimmte Anwendung zu verbessern. Beispielsweise könnte ein Ingenieur, der einen Heizkreis für eine hochpräzise Anwendung (z. B. Halbleitergehäuse) entwirft, die Verformung reduzieren.

Nächste Schritte

Sie können alle Schritte zur Modellierung eines Heizkreises sehen, indem Sie auf die Schaltfläche unten klicken. Dies führt Sie zur Anwendungsgalerie, die sowohl die Dokumentation für dieses Beispiel als auch die zugehörige MPH-Datei enthält.