Berechnung des Wärmeübergangs-koeffizienten für flache und gewellte Platten

Bei vielen technischen Anwendungen, die konjugierten Wärmetransport beinhalten, wie z.B. bei der Konstruktion von Wärmetauschern und Kühlkörpern, müssen Wärmeübergangskoeffizienten berechnet werden. Der Wärmeübergangskoeffizient wird oft mithilfe von Korrelationen und empirischen Beziehungen bestimmt und liefert Informationen über den Wärmetransport zwischen Festkörpern und Fluiden. In diesem Blog-Beitrag erörtern und demonstrieren wir, wie die Software COMSOL Multiphysics^® verwendet werden kann, um den Wärmeübergangskoeffizienten für Plattengeometrien zu ermitteln.

Was ist der Wärmeübergangskoeffizient?

Betrachten wir eine beheizte Wand oder Oberfläche, über die ein Fluid strömt. Der Wärmetransport in dem Fluid wird hauptsächlich durch Konvektion bestimmt. In ähnlicher Weise ist die Konvektion der primäre Wärmetransportmodus im Fall von zwei Fluiden (durch eine feste Oberfläche), wie zum Beispiel bei Wärmetauschern. Die Geschwindigkeit des Wärmetransports wird in beiden Fällen durch eine Temperaturdifferenz und einen Proportionalitätskoeffizienten, den Wärmeübergangskoeffizienten, beschrieben. Der Wärmeübergangskoeffizient ist ein Indikator für die Effektivität des Wärmetransports durch einen Bereich zwischen der Oberfläche und dem Fluid.

Mathematisch gesehen ist hdas Verhältnis zwischen dem Wärmestrom an der Wand und der Temperaturdifferenz zwischen der Wand und dem Fluid, d.h.,

(1)

wobei q^{\prime \prime} der Wärmestrom, T_w die Wandtemperatur, und T_\infty die charakteristische Fluidtemperatur ist.

Die charakteristische Fluidtemperatur kann auch die weit von der Wand entfernte Außentemperatur oder die mittlere Volumentemperatur (bulk temperature) in Rohren sein.

Wenn das Objekt von einem unendlich großen Luftvolumen umgeben ist, nehmen wir an, dass die Lufttemperatur weit entfernt vom Objekt ein konstanter, bekannter Wert ist. Der in diesem Fall ermittelte Wärmeübergangskoeffizient wird als externer Wärmeübergangskoeffizient bezeichnet.

Wenn wir uns die Wand genauer ansehen (wenn die Dicke der Wand in der y-Richtung definiert ist und y = 0 die Oberfläche/Ebene der Wand darstellt), wird deutlich, dass die No-Slip-Bedingung an der Wand zur Bildung eines stagnierenden, dünnen Fluidfilms führt. Der Wärmetransport durch das Fluid in unmittelbarer Nähe der Wand erfolgt daher ausschließlich durch Wärmeleitung.

Dies kann mathematisch ausgedrückt werden (Ref. 1) als:

(2)

Dabei ist k die Wärmeleitfähigkeit des Fluids, wobei die T Ableitung in dem Fluid bewertet wird.

Durch Kombination der Gleichungen (1) und (2) kann der Wärmeübergangskoeffizient wie folgt berechnet werden:

(3)

Den Wärmeübergangskoeffizienten in COMSOL Multiphysics^® berechnen

Praktisch gesehen ist es schwierig, den Temperaturgradienten an der Wand zu messen. Darüber hinaus ist es unerlässlich, für das Verständnis des Wärmetransports an der Wand einen intelligenten und rechnerisch kostengünstigen Ansatz zu analysieren. Daher werden in der Regel nicht-analytische Methoden zur Berechnung des Wärmeübergangskoeffizienten bevorzugt.

Ein gängiger Ansatz ist die Verwendung konvektiver Korrelationen, die durch die dimensionslose Nusselt-Zahl definiert sind. Diese Korrelationen liefern schnelle Ergebnisse und sind für verschiedene Fälle verfügbar, darunter natürliche und erzwungene Konvektion sowie interne und externe Strömungen. Dieser Ansatz kann jedoch nur für regelmäßige geometrische Formen, wie horizontale und vertikale Wände, Zylinder und Kugeln, angewendet werden.

Bei komplexen Formen kann der Wärmeübergangskoeffizient stattdessen durch Simulation des konjugierten Wärmetransports berechnet werden.

Betrachten wir zwei verschiedene Fälle und Ansätze:

1. Berechnung des Wärmeübergangskoeffizienten in regelmäßigen Geometrien (wie einer horizontalen Platte) mit:
   • Analyse des konjugierten Wärmetransports
   • Konvektiven Korrelationen, ohne Berücksichtigung der Strömung
2. Berechnung des Wärmeübergangskoeffizienten in unregelmäßigen/komplexen Geometrien (wie einer gewellten Platte)

Beachten Sie, dass das Strömungsregime ein wichtiger Punkt ist, da der Wärmeübergangskoeffizient von der Geschwindigkeit abhängt. In beiden Fällen muss eine pragmatische Bedingung, wie z.B. eine schnelle Strömung in einem Gebläsesystem oder einer elektronischen Chipkühlung, berücksichtigt werden. Dies zeigt, dass es notwendig ist, diese Fälle als mit Wärmetransport gekoppelte turbulente Strömung zu modellieren.

Beispiel 1: Erzwungene Konvektion und Strömung an einer horizontalen Platte

Betrachten wir die Situation der Modellierung der Strömung an einer horizontalen flachen Platte mit einer Länge von 5 m, die einem konstanten und homogenen Wärmestrom von 10 W/m² ausgesetzt ist. Die Platte befindet sich in einem Luftstrom mit einer durchschnittlichen Geschwindigkeit von 0,5 m/s und einer Temperatur von 283 K. Die Abbildung unten zeigt das Schema der Problemstellung, einschließlich der Geschwindigkeits- und Temperaturprofile für eine laminare Strömung innerhalb der Impuls- (sagen wir, \delta ) bzw. der thermischen Randschicht (\delta {T}).

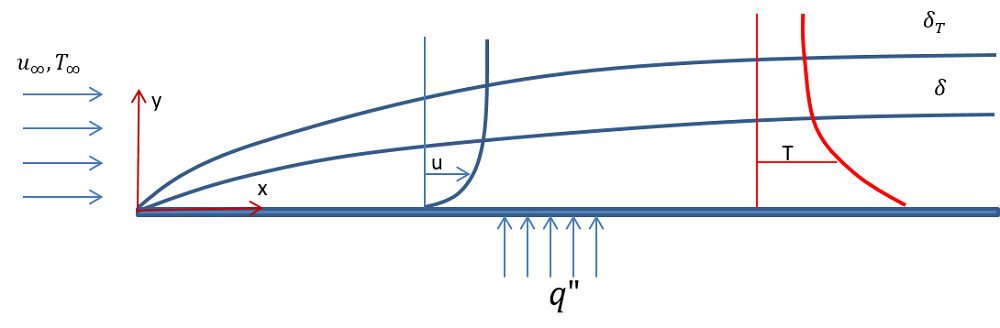
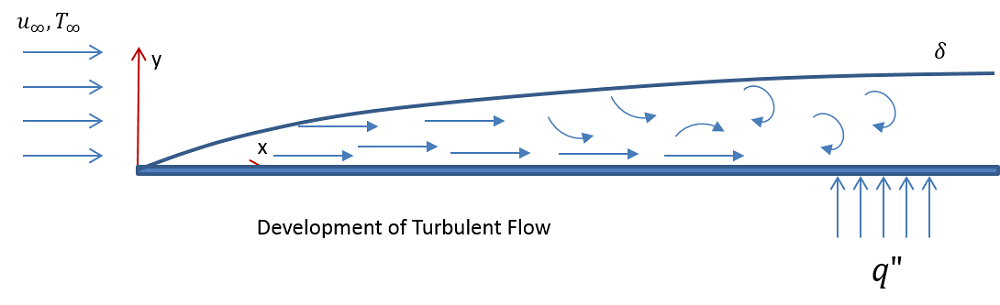
Schematische Darstellung laminarer (oben) und turbulenter Strömung (unten) an einer horizontalen Platte.

Analyse des konjugierten Wärmetransports

Die numerische Lösung wird in COMSOL Multiphysics^® mithilfe des Conjugate Heat Transfer Interface berechnet, das Strömungs- und Wärmetransportphänomene koppelt. Das Geschwindigkeitsfeld und der Druck werden nur im Luftbereich berechnet, während die Temperatur in der Platte und im Luftbereich berechnet wird.

Die Temperaturverteilung innerhalb der Platte und dem Fluid ist in der Abbildung unten dargestellt. Die thermischen und Impuls-Randschichten, die sich im Fluidbereich gebildet haben, sind in dem Bereich zu sehen, der von der Wand bis 2 cm über die Platte reicht.

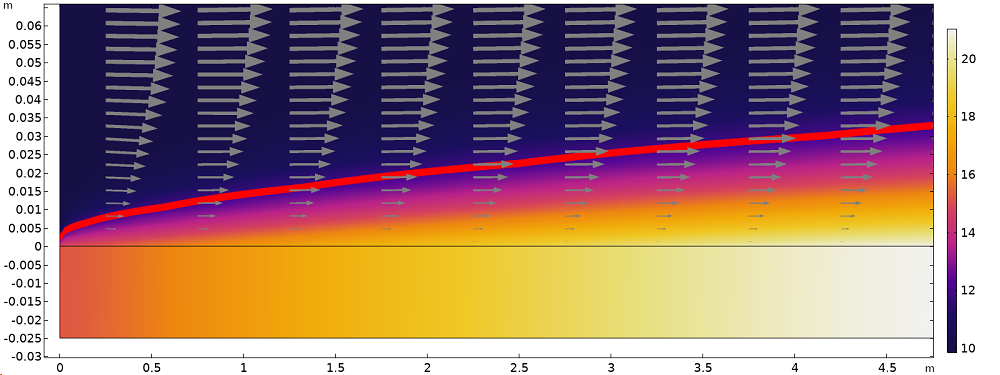
Temperaturverteilung (Oberflächendarstellung), Isotherme bei 11°C (rote Linie) und Geschwindigkeitsfeld (Pfeile), die die thermischen und Impuls-Randschichten neben der Plattenoberfläche veranschaulichen (anisotrope Achsenskala).

Aus den Simulationsergebnissen lässt sich der Wärmestrom mithilfe der entsprechenden vordefinierten Postprocessing-Variablen auswerten. Dividiert man ihn durch die Temperaturdifferenz (T_w-T_\infty), erhält man den Wärmeübergangskoeffizienten (Eq. 3). Der Wärmeübergangskoeffizient entlang der Platte, der durch die Analyse des konjugierten Wärmetransports ermittelt wurde, ist im folgenden Abschnitt in einem Diagramm dargestellt.

Der Wärmeübergangskoeffizient auf der Basis von Nusselt-Zahl-Korrelationen

Die Korrelation der Nusselt-Zahl für erzwungene Konvektion an einer flachen Platte ist in der Literatur beschrieben (zum Beispiel Ref. 1).

Bei diesem zweiten Ansatz wird dasselbe Modell gelöst, ohne die Strömung zu berücksichtigen, d.h. unter Verwendung der Korrelationen für den Wärmetransport. Der Berechnungsbereich ist auf den Festkörper (die Platte) beschränkt. Der Wärmeverlust von der heißen Platte zu dem kalten Fluid wird mit einer Heat Flux Randbedingung definiert. Diese Randbedingung enthält eine Option zur Definition des Wärmeübergangskoeffizienten mithilfe vordefinierter Nusselt-Zahl-Korrelationen, wie unten dargestellt. Beachten Sie, dass diese Korrelation in COMSOL Multiphysics^® vordefiniert ist.

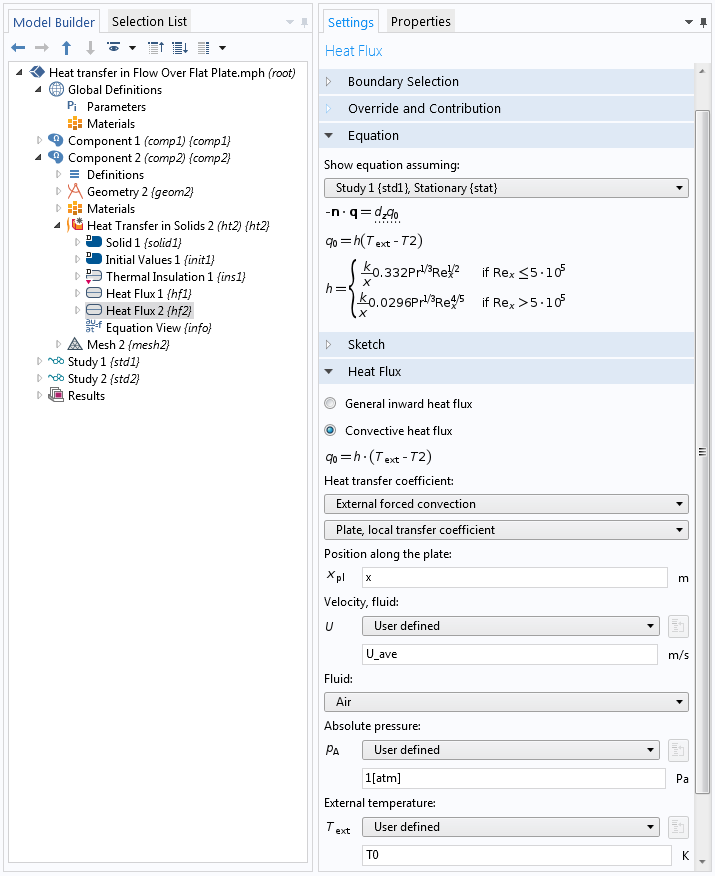
Einstellungen für die Heat Flux Randbedingung.

Nur mit diesem Ansatz wird die Temperaturverteilung in der Platte berechnet. Aus dem Wärmeübergangskoeffizienten, der in der Randbedingung Heat Flux definiert ist, lässt sich der Wärmestrom an der Plattenoberfläche, q=h\cdot(T_\infty-T), berechnen.

Evaluation des Wärmeübergangskoeffizienten

Für beide oben beschriebenen Ansätze ist es möglich, den Wärmeübergangskoeffizienten entlang der Platte zu berechnen. Die folgende Abbildung vergleicht den mit den beiden Ansätzen ermittelten Wärmestrom.

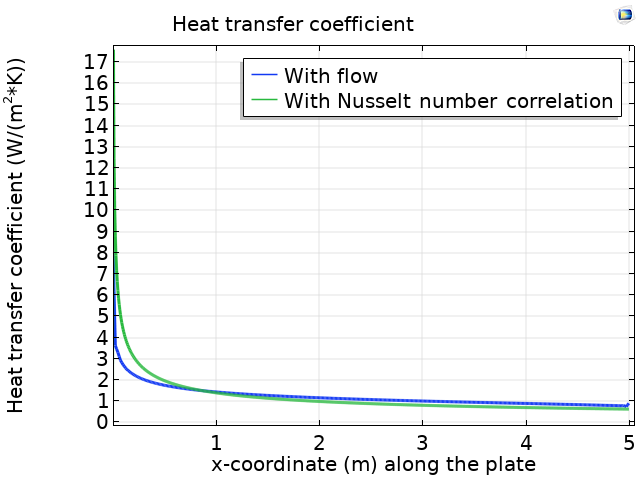Vergleich des Wärmeübergangskoeffizienten entlang der flachen Platte, der mit einer Simulation von konjugiertem Wärmetransport (blaue Linie) und einer Nusselt-Korrelation (grüne Linie) bestimmt wurde.

Wir können sehen, dass der aus der Nusselt-Zahl-Korrelation erhaltene Wert gut mit dem aus der vollständigen Simulation des konjugierten Wärmetransports erhaltenen Wert übereinstimmt.

Eine interessante Größe sind die Wärmeraten über die Platte, die in den beiden Fällen bestimmt werden:

1. Nusselt-Zahl-Korrelation: 50 W/m
2. Konjugierter Wärmetransport: 49.884 W/m

Bei bestimmten Berechnungen kann der Ansatz, der auf Nusselt-Zahl-Korrelationen basiert, den Wärmestrom mit ausreichender Genauigkeit vorhersagen. Als Nächstes untersuchen wir einen Fall mit einer ungewöhnlichen Form, bei dem die Nusselt-Zahl-Korrelationen nicht ohne weiteres verfügbar sind und der einzig mögliche Ansatz darin besteht, eine Simulation des konjugierten Wärmetransports durchzuführen.

Beispiel 2: Strömung entlang einer gewellten horizontalen Platte

Betrachten wir eine ähnliche Konfiguration wie im ersten Fall, mit dem Unterschied, dass die Platte eine gewellte Oberseite hat. Die Abbildung unten zeigt eine schematische Darstellung der Problemstellung. In diesem Modell werden die Wellen der oberen Platte in einem Abschnitt der Geometrie berücksichtigt. Der Rest der Platte ist flach.

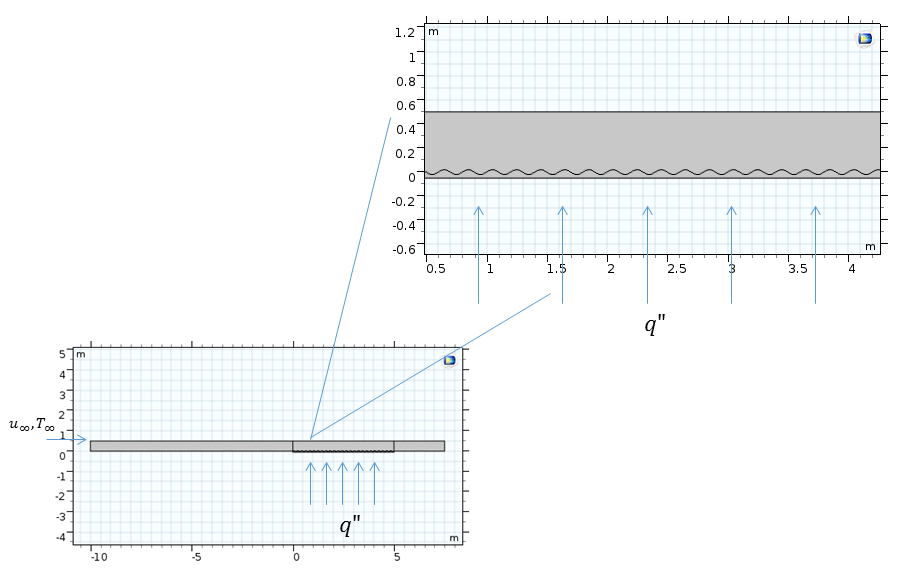
Schematische Darstellung der Strömung an einer horizontalen Platte.

Hier weist das Strömungsfeld in der Nähe der Wand Rezirkulationszonen auf, die den Wärmetransport verbessern. In der Abbildung unten sehen wir die Temperaturverteilung und die Stromlinien der Geschwindigkeit.

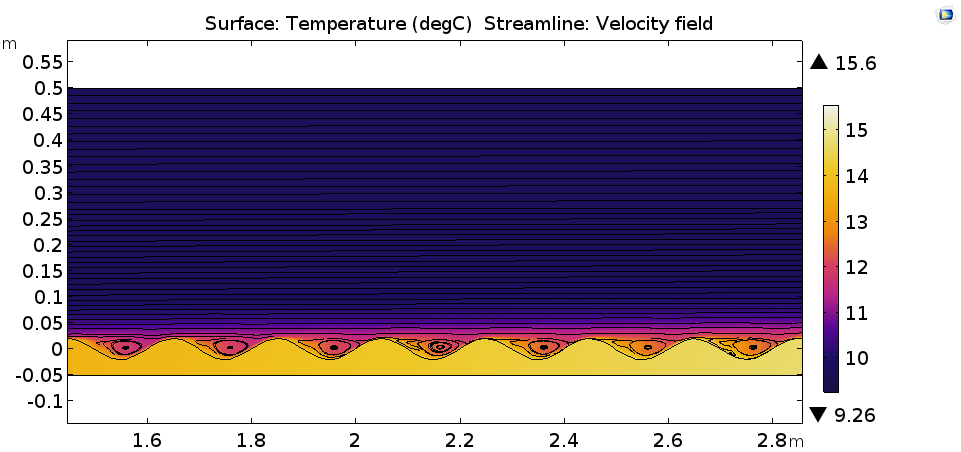
Temperaturverteilung in Grad Celsius (Oberfläche) und das Geschwindigkeitsfeld (Stromlinien).

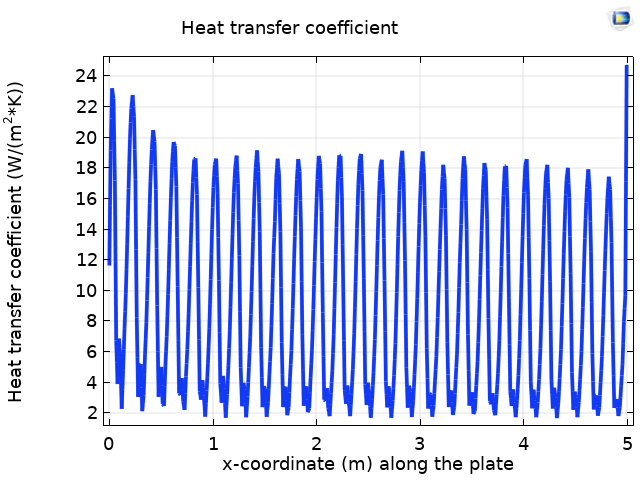
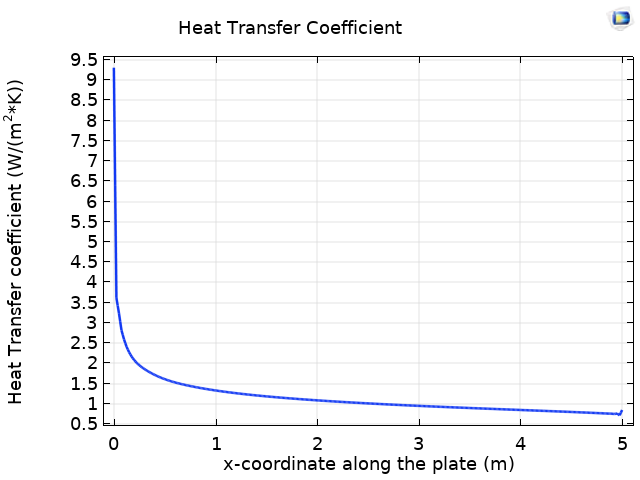
Die linke Grafik unten zeigt den Wärmeübergangskoeffizienten entlang der Länge der gewellten Platte. Bei einer Geometrie wie der der gewellten Platte ist der Wärmeübergangskoeffizient abhängig von den Temperaturfeldern, den Geschwindigkeitsfeldern und den geometrischen Parametern der Wellen, wie der Höhe. Daher können wir im Vergleich zu einer flachen Platte einen erhöhten Wärmeübergangskoeffizienten beobachten (rechtes Bild unten).

Der Wärmeübergangskoeffizient entlang der gewellten Platte (links) und entlang der flachen Platte (rechts).

Bei der Betrachtung komplexer Geometrien, die gewellte Oberflächen enthalten, kann der Ansatz des konjugierten Wärmetransports rechenintensiv sein, und alternative Ansätze sind wünschenswert. Eine gute Annäherung wäre es, die geometrische Komplexität zu reduzieren, indem man die Oberflächen als nicht gewellt darstellt und den Wärmeübergangskoeffizienten aus dieser Geometrie einer gewellten Platte extrapoliert, wobei geometrische Parameter wie die Höhe der Wellen, Strömungsgeschwindigkeitsfelder und Temperaturschwankungen auf der Oberfläche berücksichtigt werden. Interessanterweise ist der Wärmeübergangskoeffizient bei einigen Geometrien auch dann von Interesse, wenn die Temperatur nicht wirklich isotherm ist oder es keinen konstanten Wärmestrom gibt, solange die Nähe zur Ausgangskonfiguration erhalten bleibt.

Zur Überprüfung können wir einen einfachen Fall betrachten, bei dem die Wärmeübergangskoeffizienten über Geschwindigkeitsfelder in der Geometrie der gewellten Platte berechnet werden. Die Daten können verwendet werden, um einen durchschnittlichen Wärmeübergangskoeffizienten zu erhalten, und auf das Modell mit flacher Plattengeometrie extrapoliert werden. Der gesamte Wärmeverlust an der Oberfläche oder der Wärmeübergangskoeffizient aus den Strömungssimulationen können untersucht werden, um zu verstehen, wie valide diese Näherungen sind.

Abschließende Gedanken

In diesem Blog-Beitrag haben wir besprochen, wie Sie den Wärmeübergangskoeffizienten mit zwei verschiedenen Methoden berechnen können. Mit der Lösung über den konjugierten Wärmetransport können Sie die eingebauten Wärmestromvariablen verwenden, die in COMSOL Multiphysics^® verfügbar sind. Mithilfe der Randbedingung Heat Flux mit Nusselt-Zahl-Korrelationen können Sie Probleme mit einfachen Formen simulieren. Darüber hinaus haben wir besprochen, wie Sie die geometrische Komplexität reduzieren können, um den Wärmeübergangskoeffizienten für komplexe Geometrien zu ermitteln.

Nächste Schritte

Erfahren Sie mehr über die speziellen Funktionen zur Modellierung des Wärmetransports in der COMSOL^®-Software, indem Sie auf die Schaltfläche unten klicken.

Probieren Sie die hier besprochenen Ansätze in den folgenden Tutorials aus:

• Natural Convection Cooling of a Vacuum Flask
• Nonisothermal Turbulent Flow Over a Flat Plate
• Nonisothermal Laminar Flow in a Circular Tube

Referenz

1. A. Bejan et al., Heat Transfer Handbook, John Wiley & Sons, 2003.