Veröffentlichungen und Präsentationen

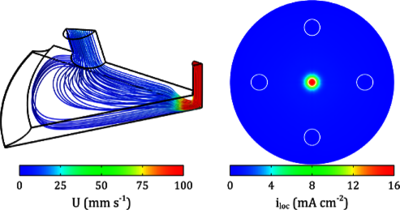
Electrochemical flow cells have found widespread use in analytical chemistry due to their short response time, high sensitivity and selectivity. The geometrical flexibility and therefore, the ease of coupling the electrochemical to other experimental techniques has attracted considerable interest for applications in electrocatalytic research as well. Such coupling is far more cumbersome with the rotating disk electrodes (RDEs) often used in this field. In this study, we model laminar flow velocity profiles of electrochemical flow cells featuring flow profile elements from both channel and wall-jet electrodes. The above is coupled to the Nernst-Planck equation describing the transport of diluted species towards an electrode surface represented as an equation based species flux following the Butler-Volmer equation. We will present a novel numerical approach to obtain a modified Koutecký-Levich equation for electrochemical flow cells with complex geometries containing elements of both fluid profiles of wall-jet and channel electrodes.