support@comsol.com
Neuerungen für Studien und Löser
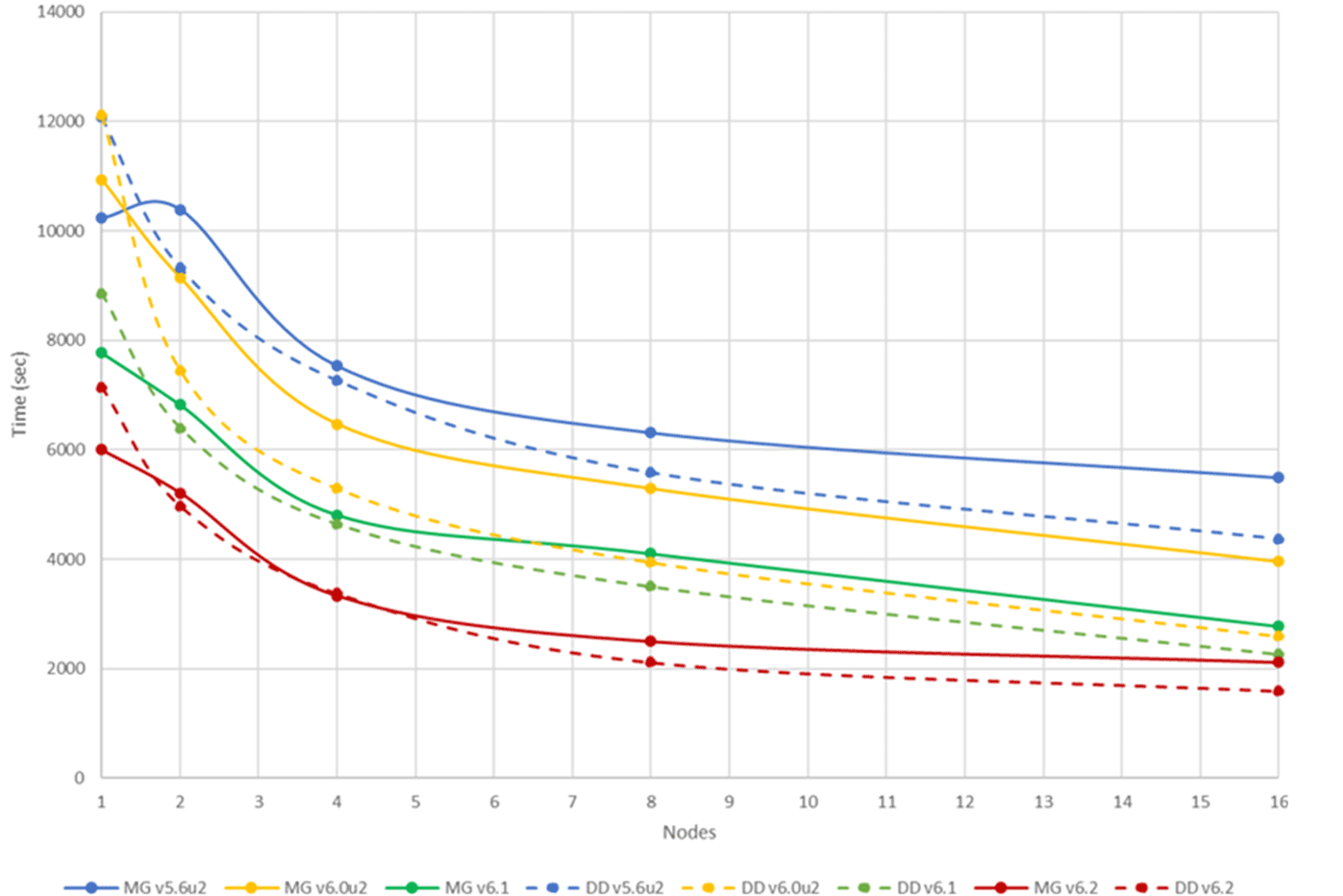
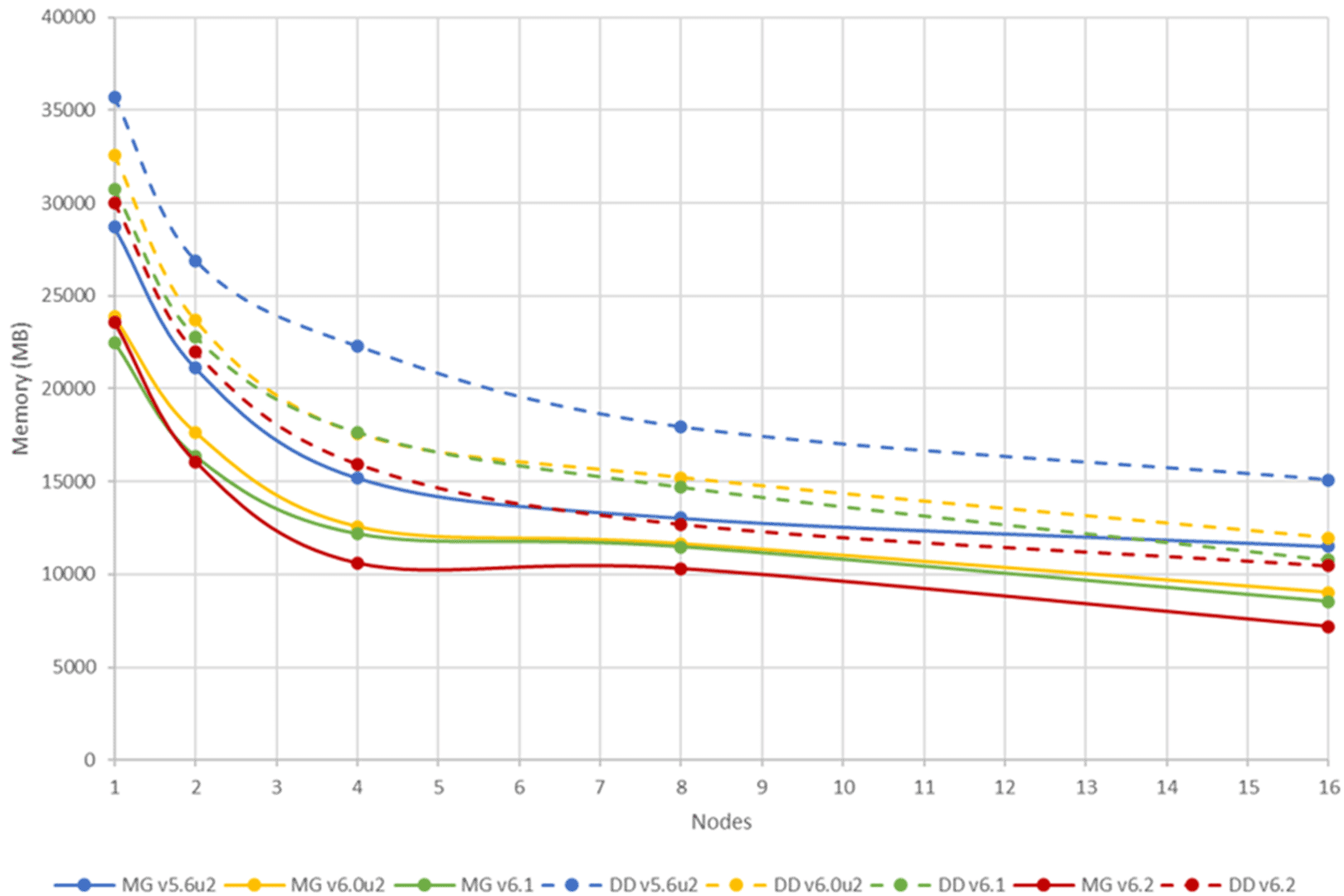
COMSOL Multiphysics® Version 6.2 führt viele Leistungsverbesserungen ein, insbesondere für nichtlineare Probleme und paralleles Rechnen. Darüber hinaus wurde die Randelemente-Methode (BEM) für die Hochfrequenz-Elektromagnetik sowie für Probleme mit schmalen Lücken verbessert. Zudem besteht jetzt Unterstützung für die zeitliche Periodizität von Variablen, die nicht gelöst werden. Eine Option zur Verwendung einer Fast-Fourier-Transformation (FFT) für antisymmetrische Probleme wurde hinzugefügt, und die neue Unterstützung für linke Eigenvektoren eignet sich für die Modellreduktion und die Sensitivitätsanalyse von nicht-symmetrischen Problemen. Hier erfahren Sie mehr über alle Updates.Verbesserte Cluster- und Multicore-Leistung
In COMSOL Multiphysics® Version 6.2 gibt es eine Verbesserung von bis zu 40% für Cluster und Multicore-Computing. Der BEM-Speicherausgleich und die Leistung auf Clustern wurden erheblich verbessert.
Neue Methode für die Handhabung von Nebenbedingungen
Eine neue hybride Methode zur Behandlung von Nebenbedingungen wurde hinzugefügt. Diese Methode verwendet das Gaußsche Eliminationsverfahren für größere Bedingungsblöcke, bei denen eine vollständige Singulärwertzerlegung zu aufwändig ist, während für kleinere Blöcke weiterhin eine Singulärwertzerlegung verwendet wird. Dies ist besonders nützlich bei großen Simulationen mit nichtlokalen Nebenbedingungen.
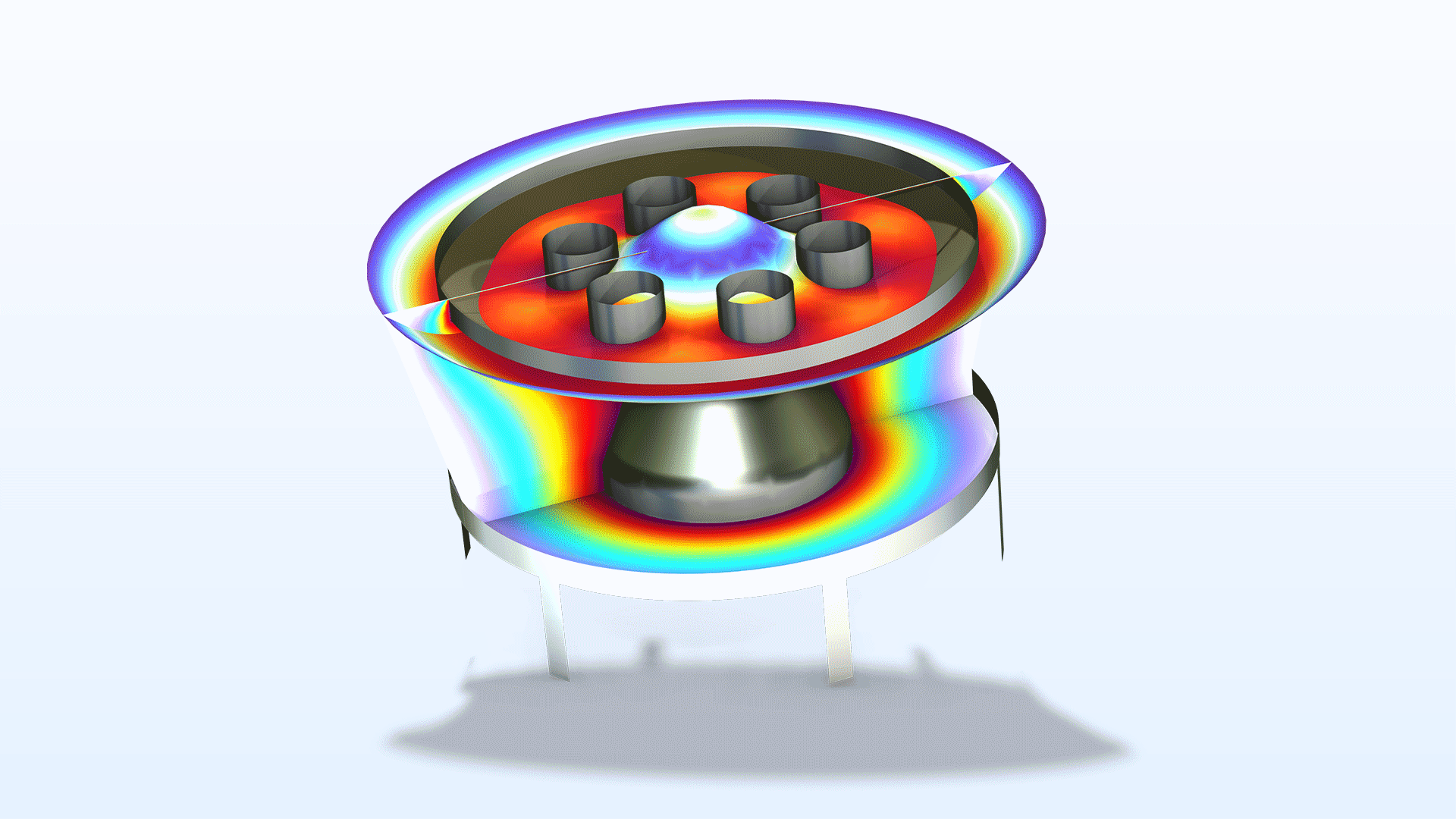
Periodisches Input
Bei Simulationen, die die sequentielle Lösung eines zeitperiodischen Problems und eines transienten Problems erfordern, ist es jetzt nur noch notwendig, eine Periode des periodischen Feldes zu simulieren. Diese Funktionalität kann direkt im Abschnitt Advanced des Knotens Time-Dependent Solver aktiviert werden. Sie können damit eine einzelne Periode einer rotierenden Maschine simulieren und dann für andere Felder, die zeitabhängig sind, auf Zeitskalen lösen, die größer sind als eine einzelne Maschinenumdrehung.

Unterstützung für Halbzyklus-FFT
Es ist jetzt möglich, eine FFT für antisymmetrische Probleme zu berechnen, indem nur die erste Hälfte der Signaldaten verwendet wird. Bei großen transienten Modellen kann die Berechnungszeit halbiert werden, da für die Durchführung der FFT nicht mehr eine ganze Periode berechnet werden muss.
Randelemente-Methode (BEM)
Leistungsverbesserungen
Die Durchführung von BEM-Analysen auf Clustern ist jetzt bis zu 7-mal schneller als in früheren Softwareversionen. Dies ist auf den verbesserten Last- und Speicherausgleich in COMSOL Multiphysics® Version 6.2 zurückzuführen. Auf Nicht-Cluster-Konfigurationen reduziert ein verbesserter Löser die Berechnungszeit um bis zu 35%.
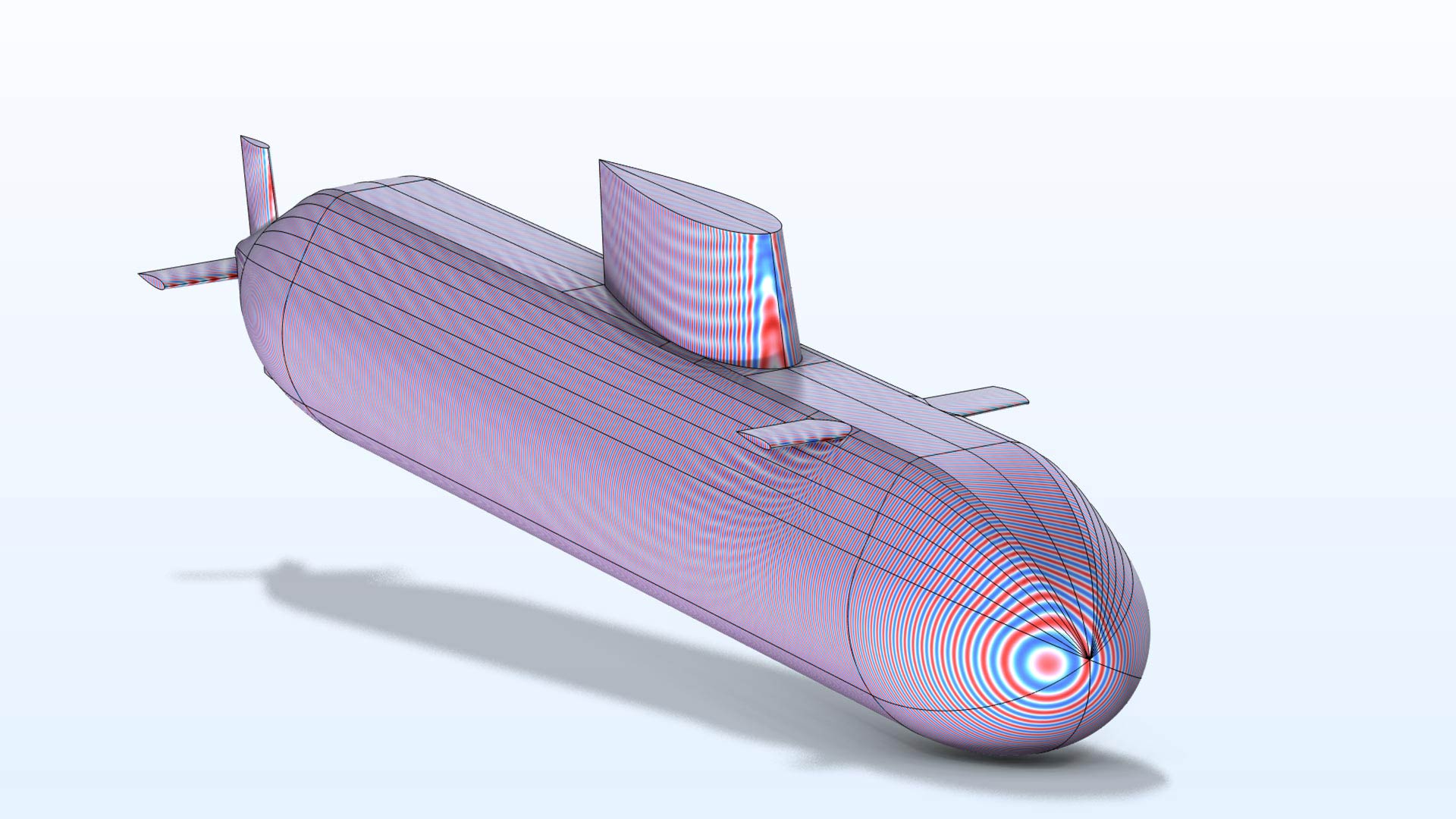
Spezielle Quadratur für nahe beieinander liegende Netzelemente
Die Option Thin gap handling im Abschnitt Quadrature ermöglicht eine variable Transformation auf sich fast berührenden Netzelementen, die eine genauere Integration ermöglicht. Diese Transformation führt zu erheblichen Genauigkeitsverbesserungen bei Problemen, die schmale Lücken enthalten, zum Beispiel bei Problemen mit Kondensatoren oder Schallabstrahlung durch dünne Wellenleiter.
Neue Optionen für den nichtlinearen Löser
Es wurden viele neue Optionen hinzugefügt, um die Leistung oder die Robustheit des nichtlinearen Lösers zu optimieren. Bei der Pseudo-Time-Stepping-Beschleunigung wurde festgestellt, dass die neue Option zur Glättung der Residuen die Anzahl der nichtlinearen Iterationen reduziert. Für den Proportional-Integral-Derivative- (PID-) Regler sind mehrere neue Optionen verfügbar. Für Transportprobleme wurde die Anderson-Beschleunigung verbessert und eine Option hinzugefügt, die steuert, wann der Anderson-Schritt anstelle eines regulären Newton-Schrittes verwendet wird. Die oben erwähnten Verbesserungen sorgen zusammen für eine erheblich verbesserte Leistung.
Verbesserungen von Jacobian update
Bei zeitabhängigen Problemen kann die Jacobi-Matrix automatisch aktualisiert werden, indem Sie die Option Jacobian update im Knoten Fully Coupled oder im Variablenknoten Segregated Solver auf Minimal setzen. Dies führt zu einer verbesserten Leistung, ohne die Robustheit zu gefährden. Ein neuer, robusterer Algorithmus bestimmt, wann die Jakobi-Matrix aktualisiert werden sollte, und ist standardmäßig aktiviert. Das Kästchen Use linear heuristics for adaptive tolerance deaktiviert den neuen Algorithmus und nutzt stattdessen den in COMSOL Multiphysics® Version 6.1 verfügbaren Algorithmus.
Adaptive Toleranz für den linearen Löser
Es gibt jetzt eine Option zur Verwendung einer adaptiven Toleranz für den linearen Löser. Obwohl die Anzahl der nichtlinearen Iterationen steigen kann, kann die Anzahl der linearen Iterationen pro nichtlinearer Iteration drastisch sinken, was zu erheblichen Leistungssteigerungen führt. Die Anpassung basiert entweder auf vollständigen oder partiellen Fehlerschätzungen oder auf dem nichtlinearen Residuum. Diese Option ist unter dem Löser-Knoten Fully Coupled oder dem Variablenknoten Segregated Solver verfügbar.
Berechnung linker Eigenvektoren
Viele Multiphysik-Probleme - zum Beispiel Akustik-Struktur-Interaktionen - können nicht-symmetrische Formulierungen haben. Die Modellreduktion, Optimierung und Sensitivitätsanalyse solcher Probleme kann durch die Verwendung von linken Eigenvektoren verbessert werden. Die Option Compute and store left eigenvectors unter dem Knoten Eigenvalue Solver steuert, ob linke Eigenvektoren berechnet und eventuell gespeichert werden. Sowohl der Eigenwert-Sensitivitäts-Löser als auch der modale Löser können jetzt linke Eigenvektoren verwenden. Die Option Compute and store left eigenvectors ist standardmäßig aktiviert, wenn auf den Eigenwert-Löser ein modaler oder Modellreduktions-Löser folgt.
Neue Möglichkeit zum Speichern von Variablen im Output
Die Option zum Speichern von Variablen im Output wurde aus dem Abschnitt Values of Dependent Variables des Studienschritts in einen eigenen Abschnitt Store in Output verschoben. In diesem Abschnitt können Sie auf einfache Weise festlegen, welche Variablen gespeichert werden sollen.
Speichern des Löser-Protokolls
Das im Fenster Log angezeigte Löser-Protokoll ist auf eine bestimmte Anzahl von Zeichen begrenzt. Die maximale Anzahl der Zeichen kann unter Preferences erhöht werden. Bei der Fehlersuche in größeren Modellen kann es jedoch praktischer sein, das Protokoll stattdessen in einer Datei zu speichern. Diese Option ist jetzt im Abschnitt Log and Messages des Fensters Preferences verfügbar.