Mechanical Damage Models for Concrete
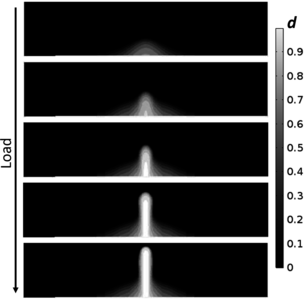
Damage models can be used to simulate the quasi-brittle behaviour of cementitious materials, since they can represent cracking in a smeared-way under various loading conditions. COMSOL Multiphysics® developed a functionality to access external material models for structural mechanics in a post by González (2015). We present a different implementation of the same model, using a generic physics (Domain Ordinary Differential Equation) and a specific solver configuration to allow for storing the history variables. The main feature of the implementation is the definition of two history variables. Two additional degrees of freedom (DOFs) are added through this new physics. The main advantages of the new implementation are that: (1) it can be fully coupled with other physics and any other constitutive law, (2) all variables are readily available within the COMSOL Multiphysics® interface, thus facilitating the post-process of results, and (3) the mechanical damage model is easier to adjust or reformulate, without the need of code compilation. The use of damage models for simulation of nonlinear stress-strain response including the softening regime has the disadvantage that the results are mesh dependent. To remedy this, a gradient-enhanced formulation developed by Peerlings et al. (1996) has been implemented in COMSOL Multiphysics® through the Helmholtz equation interface. The regularized implementation has been used to simulate a classical 3-point bending beam test. Results are in good agreement with those from other authors, and are shown to be mesh independent. Based on Mazars’ damage model (Mazars, 1986) a new formulation named “μ model” has been recently proposed (Mazars et al., 2015). The improvements of this formulation include among others a more accurate representation of concrete behaviour under biaxial and triaxial compression. We implemented the μ model in COMSOL Multiphysics® using a similar setup as the one described for the Mazars’ damage model. The results of both models under plane stress conditions for different biaxial loads are compared to classical experimental data from Kupfer et al. (1969). The comparison shows a clear improvement in strength prediction with the latter. Improvements under triaxial stresses (confinement levels of 0, 20, 35, 50 and 100 MPa) are also clearly appreciated through triaxial tests simulations. The implemented models can predict concrete mechanical behaviour under confined conditions and can be readily coupled with other mechanical processes, as well as chemical degradation or hydraulic and thermal processes.
References: González E, 2015. Accessing External Material Models for Structural Mechanics. COMSOL Blog December 2015, accessible at: https://www.comsol.com/blogs/accessing-external-material-models-for-structural-mechanics/ Kupfer H, Hilsdorf H K, Rusch H, 1969. Behaviour of concrete under biaxial stresses. Journal of the American Concrete Institute, 66, 656–666. Mazars J, 1986. A description of micro- and macroscale damage of concrete structures. Engineering Fracture Mechanics, 25(5–6), 729-737. Mazars J, Hamon F, Grange S, 2015. A new 3D damage model for concrete under monotonic, cyclic and dynamic loadings. Materials and Structures, 48, 3779–3793. Peerlings R, de Borst R, Brekelmans W, de Vree J, 1996. Gradient-enhanced damage for quasi-brittle materials. Int. J. for Numerical Methods in Engng., 39, 3391-3403.
Herunterladen
- laviña_presentation.pdf - 1.6MB
- laviña_poster.pdf - 1.15MB
- laviña_abstract.pdf - 0.13MB
