Veröffentlichungen und Präsentationen

Introduction: Modeling biological structures is challenging due to their often complex anatomical geometries and material properties. Finite element studies of the femur, the largest and strongest bone in the human body, have focused on the femoral neck, since this is where fractures often occur. This study developed COMSOL finite element models of the human femur diaphysis (shaft), subjected to anatomical loading. Models were developed from a simple, hollow cylinder; to an anatomical, but uniform, cross section; to an anatomically correct model with eleven cross sections. Models were subjected to physiologically relevant axial, torsional, and bending loads. The calculated stresses and deformations were used to quantitatively compare the models. Results show the importance of anatomical geometry in biomechanical models.

Keywords: Femur diaphysis, anatomical cross sections, COMSOL Multiphysics, 3D lofting of profiles, solid mechanics, axial compression, torsion, bending, von Mises stresses, deflections.

COMSOL Multiphysics Model: The anatomical femur cross section was built using medical CT scan data from the literature [1]. Data points defining the outer perimeter (periosteum) and inner perimeter (endosteum) were digitized from these scans. Work planes were defined for the outer and inner perimeters for each of the 11 cross sections. Figure 1 shows three representative femur cross sections. Perimeter profiles were contoured by vertex projection and then lofted into a 3D solid. The interior lofted solid was subtracted from the exterior lofted solid, giving the final geometry. The models were constrained at one end and loaded at the other for the three cases of axial compression, torsion, and bending. A physics-controlled mesh and a stationary analysis were performed. The model used isotropic material properties of cortical bone with elastic modulus of 17.4 GPa, Poisson’s ratio of 0.39, and density of 1908 kg/m3 [2].

Results: Axial Compression Femur models were fixed at the distal end and loaded with a physiologically realistic axial compressive load of 70 kg/2 at the proximal end. Maximum von Mises stress for the solid and hollow cylinder models agreed with hand calculations (not shown). Maximum von Mises stress for the one-section anatomical model were also as expected (load/cross section). The full femur model subjected to axial compressive loading exhibited three high stress areas that arise due to the non prismatic nature of this model. For all four models, maximum stress is below the ultimate compressive, longitudinal stress for cortical bone, 195 MPa, and displacement is negligible.

Torsion The four femur models were loaded with a 200 Nm load at the distal end. This load does not correspond to normal physiological conditions, but might arise, for example, by a torque produced at the end of a ski. Again, results for the solid and hollow cylinder models agree with hand calculations. As expected, von Mises stresses for these two models is uniform for a given radius.

Figure 2 shows von Mises stresses for the one section model. The longitudinal red strip shows a high stress region arising from the asymmetric anatomical cross section. Stress in this region is 127 MPa, which exceeds the ultimate shear stress for cortical bone, 69 MPa. Maximum displacement for this model is 3.52 mm.

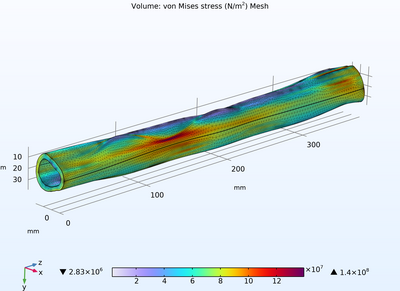
Figure 3 shows von Mises stresses for the full 11 section femur model. High stress regions arise from the anatomical structure, with peak of 148 MPa, far exceeding the ultimate shear stress for cortical bone of 69 MPa. Maximum displacement for this model is 3.53 mm, virtually the same as for the one section model.

Bending The four femur models were loaded with a 200 N transverse load at the distal end. This load does not correspond to normal physiological conditions, but might arise, for example, by the lower leg being fixed by terrain and the upper body continuing to move forward in three-point bending, as in a so-called “boot top” fracture. Once again, results for the solid and hollow cylinder models agreed with hand calculations. For all four models, maximum von Mises stress was below the ultimate bending normal stress for cortical bone, 209 MPa.

Conclusion: Using CT scan data to define cross-sectional geometry provides a more anatomically correct model of the human femur diaphysis than a simple assumed geometry. The asymmetry of the anatomical cross section is especially important for torsion and bending loads, with the femur more resistant to bending in the anterior/posterior direction than the medial/lateral direction. These results can help predict femur injury and, ultimately, fracture. Results show the importance of anatomical geometry in biomechanical models.