
Gastblogger Björn Fallqvist von Lightness by Design erörtert verschiedene Überlegungen und Ansätze zur Analyse der thermomechanischen Ermüdung.
In diesem Blog-Beitrag untersuchen wir die relevanten Materialmodelle in der Software COMSOL Multiphysics® für die thermomechanische Ermüdungsanalyse. Experimentelle Daten aus thermomechanischen Ermüdungsversuchen werden zusammen mit Materialparametern aus der referenzierten Literatur verwendet. Anschließend wird ein bei erhöhten Temperaturen betriebener Druckbehälter analysiert und ein nichtlineares kontinuierliches Ermüdungsschädigungsmodell wird zur Einschätzung der Ermüdungslebensdauer verwendet.
Warum eine Analyse der thermomechanischen Ermüdung?
Für viele Anwendungen ist die herkömmliche isotherme Ermüdungsanalyse nicht ausreichend, da die Bauteile bei erhöhten Temperaturen arbeiten oder zyklisch zwischen diesen Temperaturen wechseln und sich das Materialverhalten erheblich von der Raumtemperatur unterscheidet. Turbinen und Kraftwerkskomponenten sind typische Beispiele für solche Anwendungen.
Bei der konventionellen Ermüdungsanalyse, insbesondere bei High-Cycle-Fatigue (HCF), werden die Auswirkungen hoher Temperaturen nicht direkt berücksichtigt. Im HCF-Bereich sind die Belastungen gering und Effekte wie Kriechen werden als vernachlässigbar angesehen. Manchmal wird eine Reduzierung der S-N-Kurve vorgenommen, um die geringere Ermüdungsfestigkeit bei erhöhter Temperatur zu berücksichtigen. Dabei werden jedoch die Auswirkungen gleichzeitiger Temperatur- und Lastwechsel, die als thermomechanische Ermüdung bezeichnet werden, nicht berücksichtigt. Der Einfluss dieser Temperaturschwankungen ist besonders im Bereich des Low-Cycle-Fatigue (LCF) von Bedeutung, wo mehrere Aspekte berücksichtigt werden müssen – in erster Linie die Variation der Materialeigenschaften für Elastoplastizität und Kriechen.
Eine Möglichkeit zur Bewertung der Ermüdungsfestigkeit bei erhöhten Temperaturen besteht darin, die stabilisierte Spannungs-Dehnungs-Kurve (oft in der Mitte der Lebensdauer) einer Probe bei verschiedenen Temperaturen zu verwenden, um eine Spannungs- oder Dehnungsamplitude zu erhalten und die Verfestigungsparameter zu bestimmen, die die nichtlineare Spannungs-Dehnungs-Kurve steuern. Theoretisch könnte man dann Experimente mit einer bestimmten Kombination von angewandter Last und Temperatur durchführen und versuchen, die Ermüdungslebensdauer anhand der experimentellen Ergebnisse abzuschätzen. Thermomechanische Ermüdungsversuche sind jedoch relativ zeitaufwendig und kostspielig. Eine praktikablere Methode zur Abschätzung der Ermüdungsfestigkeit bei erhöhten Temperaturen ist die Verwendung eines analytischen Ausdrucks für die Beziehung zwischen Spannungsniveaus und Zyklen bis zum Versagen und dessen Korrektur hinsichtlich der Temperatur.
Thermomechanische Ermüdungsprüfung
Bei der thermomechanischen Ermüdungsprüfung wird eine Probe in der Regel gleichzeitig einer zyklischen Dehnung und einer zyklisch wechselnden Temperatur ausgesetzt. Dies kann entweder phasengleich oder phasenverschoben erfolgen. Im ersten Fall tritt die maximale Zugbelastung gleichzeitig mit der maximalen Temperatur auf, im zweiten Fall tritt die maximale Zugbelastung bei der minimalen Temperatur auf.
Zum Vergleich mit den experimentellen Ergebnissen in diesem Blog-Beitrag verweisen wir auf Ref. 1, wo die thermoplastische Ermüdung eines P91 (ein gängiger Kraftwerksstahl) untersucht wurde. Es wurden Spannungs-Dehnungs-Kurven ermittelt und die Parameter des Materialmodells wurden aus Ref. 2 übernommen. Für die referenzierte Arbeit wird ein einheitliches Modell verwendet (das heißt die viskoplastischen Dehnungen setzen sich sowohl aus den plastischen als auch aus den Kriechkomponenten zusammen). Dies wirkt sich jedoch nur auf die Werte des Kriechanteils des Modells aus.
Materialmodelle für thermomechanische Ermüdungsanalysen
Die Parameter des Materialmodells als Funktion der Temperatur (Ref. 2) lauten:
| Temp [°C] | E [MPa] | k [MPa] | Q [MPa] | b [-] | a1 [MPa] | C1 [-] | a2 [MPa] | C2 [-] | Z [MPa s1/n] | n [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 187,537.0 | 96 | -55.0 | 0.45 | 150.0 | 2350.0 | 120.0 | 405.0 | 2000 | 2.25 |
| 500 | 181,321.6 | 90 | -60.0 | 0.6 | 98.5 | 2191.6 | 104.7 | 460.7 | 1875 | 2.55 |
| 600 | 139,395.2 | 85 | -75.4 | 1.0 | 52.0 | 2055.0 | 463.0 | 463.0 | 1750 | 2.7 |
Tabelle 1. Materialparameter aus der Referenz.
Die Parameter a und C beziehen sich auf das nichtlineare kinematische Verfestigungsmodell, E ist der Elastizitätsmodul, k ist die anfängliche Fließspannung, Q und b sind isotrope Verfestigungsparameter und Z und n sind Materialparameter für das viskoplastische Fließverhalten.
Diese werden in den folgenden Abschnitten näher erläutert. Zusammen bestimmen diese Parameter die Translation und Expansion/Kontraktion der Fließfläche im Spannungsraum. Alle Werte der Modellparameter werden zwischen den Temperaturen interpoliert. Die Durchführung dieses Verfahrens wird in den folgenden Abschnitten gezeigt.
Viskoplastizität
Ratenabhängige Effekte werden durch die Verwendung der viskoplastischen Chaboche-Formulierung für die Rate des viskoplastischen Dehnungstensors \dot{\epsilon}_{vp} gemäß Ref. 5 berücksichtigt.
wobei A ein Ratenfaktor (gleich 1/s), F die Fließfunktion, nD die Tensorrichtung des Spannungsdeviators, n ein Materialparameter und \sigma_{ref} ein Referenzspannungswert ist.
Die Parameter σref und n von COMSOL Multiphysics entsprechen Z bzw. n in Tabelle 1. Die Fließfunktion F ist definiert als
Dabei ist R die Zunahme der Fließfläche, k die anfängliche Fließspannung und \sigma_b der Rückspannungstensor aufgrund der kinematischen Verfestigung.
Die Funktion φ wird als die Von-Mises-Vergleichsspannung gewählt.
Isotrope Verfestigung
Das isotrope Verfestigungsgesetz (Voce) für die Fließflächengröße σy ist definiert als
wobei σsat eine Sättigungsspannung für die Fließflächengröße bei großen plastischen Dehnungen, β ein Materialparameter und \epsilon_{vp,e} die äquivalente viskoplastische Dehnung ist.
Bei dieser Formulierung kann sich die Fließfläche je nach Wert der Sättigungsspannung mit zunehmender plastischer Dehnung entweder ausdehnen oder zusammenziehen. Die Parameter σsat und β in COMSOL Multiphysics entsprechen Q bzw. b in Tabelle 1.
Kinematische Verfestigung
Das gewählte nichtlineare kinematische Verfestigungsgesetz ist ein Verfestigungsgesetz nach Chaboche, bei dem der Rückspannungstensor aus einer Anzahl j überlagerter Zweige der nichtlinearen Armstrong-Frederick-Verfestigungsterme besteht:
Der erste Term mit einem anfänglichen kinematischen Verfestigungsmodul wird in unseren Analysen ignoriert. Im Vergleich zur Formulierung in Ref. 1-2 sind die Verfestigungsparameter C und γ für die beiden Zweige in COMSOL Multiphysics® Ca bzw. C.
Kriechen
Wie bereits erwähnt, verwenden die Autoren in den referenzierten Artikeln ein vereinheitlichtes viskoplastisches Modell, und die viskose Spannung wird direkt definiert. In COMSOL Multiphysics® wird das Kriechmodell von Norton für die Kriechdehnungsrate verwendet:
Dabei ist Ac ein Ratenfaktor, σeff die Vergleichsspannung, σref ein Vergleichsspannungswert (festgelegt auf 1 MPa) und nc ein Materialparameter. Die Werte dieser Parameter wurden Ref. 6 entnommen.
Materialparameter zur Verwendung in COMSOL Multiphysics®
Die in den Analysen verwendeten Materialparameter sind nachfolgend zusammengefasst. Die Namen der Parameter wurden in den meisten Fällen an die Bezeichnungen in COMSOL Multiphysics® angepasst. Außerdem unterscheidet sich die Definition der Konstanten C von der im zitierten Artikel verwendeten, weshalb sie einen anderen Wert annehmen.
| Temp [°C] | E [MPa] | \sigma_{ys0} [MPa] | \sigma_{sat} [MPa] | β [-] | C_1 [MPa] | \gamma_1 [-] | C_2 [MPa] | \gamma_2 [-] | \sigma_{ref,vp} [MPa s1/n] | n [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 187,537.0 | 96 | -55.0 | 0.45 | 352,500 | 2350.0 | 810,000 | 405.0 | 2000 | 2.25 |
| 500 | 181,321.6 | 90 | -60.0 | 0.6 | 215,870 | 2191.6 | 863,810 | 460.7 | 1875 | 2.55 |
| 600 | 139,395.2 | 85 | -75.4 | 1.0 | 106,860 | 2055.0 | 810,250 | 463.0 | 1750 | 2.7 |
Tabelle 2. Materialparameter zur Verwendung in COMSOL Multiphysics®.
Die Kriechparameter A_c=2,4623 \cdot 10^{-21}/h, \sigma_{ref,cr}=1 MPa und n_c=7. 538 sowie die Querkontraktionszahl von 0,3 und der Wärmeausdehnungskoeffizient \alpha=14,5 \cdot 10^{-6}/^{\circ}C waren für alle Temperaturen gleich. Die Kriechparameter wurden bei 873 K gemessen, wobei in COMSOL Multiphysics® auch eine Temperaturabhängigkeit berücksichtigt werden kann.
Nichtlineares Modell der kontinuierlichen Schädigung und Ermüdung
Hintergrund
Das für die Ermüdungsanalyse verwendete Ermüdungsmodell ist das nichtlineare kontinuierliche Ermüdungsschädigungsmodell nach Chaboche (Ref. 3). Dieses Modell ist einfach zu handhaben und gilt sowohl für die Ermüdung bei niedrigen als auch bei hohen Zyklen (für Stähle). Es basiert auf einer Schädigungsratengleichung der Form
Die Schädigungsrate D bezogen auf die Zyklenzahl N hängt von der maximalen Spannung \sigma_M, der mittleren Spannung \bar\sigma und der aktuellen Schädigung ab. Für eine gegebene Funktion f erhält man eine Gleichung für die Anzahl der Zyklen bis zum Versagen, NF (Herleitung hier weggelassen):
wobei a und \beta_{fat} Materialparameter, \sigma_u die Zugfestigkeit und \sigma_l die Ermüdungsgrenze für die mittlere Spannung \bar\sigma sind gemäß
Dabei ist b_{fat} ein Materialparameter.
Schließlich ist M\bar{(\sigma)} definiert als
mit M_0 als Materialparameter.
Bei der thermomechanischen Ermüdung mit schwankender Temperatur T kann die effektive Temperatur (T*) während eines Zyklus berechnet werden mit
Im Wesentlichen wird die effektive Temperatur T* als diejenige Temperatur betrachtet, für die die gleiche Anzahl von Zyklen NF berechnet wird, wie die durchschnittliche Anzahl von Zyklen über eine Zeitspanne \Delta t zwischen den Extremtemperaturen.
Ermüdungsdaten und Annahmen
Bei Raumtemperatur beträgt die Zugfestigkeit von Stahl P91 600 MPa (Ref. 7) und die Ermüdungsgrenze etwa 420 MPa, entnommen aus Ref. 6 zusammen mit der Anzahl der Zyklen bis zum Versagen bei verschiedenen Spannungsniveaus. Diese können zur Bestimmung der S-N-Kurve nach dem Ermüdungsmodell von Chaboche (Abbildung 1) mittels der Methode der kleinsten Quadrate verwendet werden. Das Belastungsverhältnis R (R=\frac{\sigma_{min}}{\sigma_{max}}, Verhältnis von minimaler zu maximaler Spannung) ist hier R = -1, das heißt \bar\sigma=0. Für die Parameterbestimmung gilt M\bar{(\sigma)}=M_0 und \sigma_l(\bar\sigma)=\sigma_{l0}.
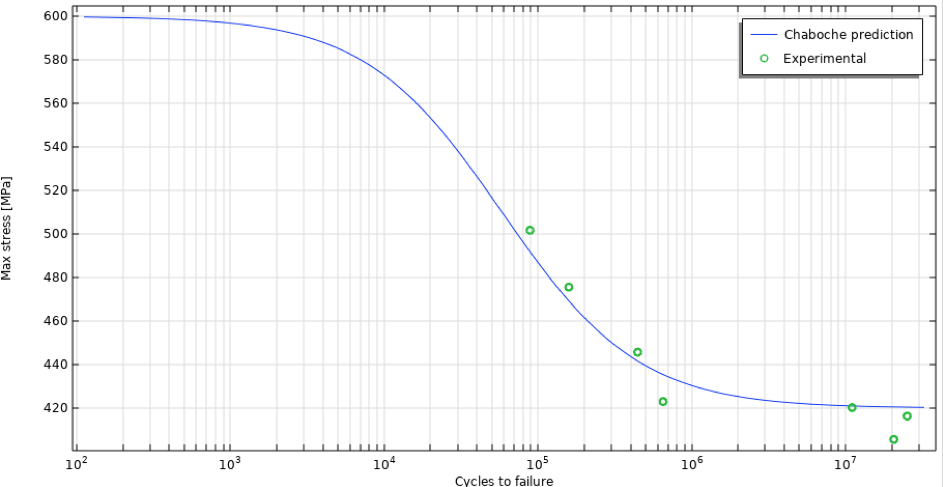
Abbildung 1. S-N-Kurve nach dem Ermüdungsmodell von Chaboche.
Die resultierenden Parameter sind a = 9 \cdot 10^{-6}, \beta_{fat}=0.287 und M_0=54.3 MPa.
Idealerweise werden mehr Punkte im Zwischenbereich benötigt, um die Kurve vollständig zu definieren, aber für eine Demonstration der Methode ist dies ausreichend. Da die Berücksichtigung thermischer Effekte entscheidend ist, muss die S-N-Kurve skaliert werden. Dazu gibt es mehrere Möglichkeiten; die geeignetste wäre, Kurven bei verschiedenen Temperaturen zu verwenden, Materialparameter für jede Temperatur zu erhalten und diese zu interpolieren. Wenn solche Daten nicht verfügbar sind, eignet sich auch eine Skalierung der Zugfestigkeit und der Ermüdungsgrenze mit den in Abbildung 3.24 in Ref. 1 definierten Reduktionsfaktoren. Die resultierenden S-N-Kurven sind in Abbildung 2 dargestellt. Sie gelten alle für R = -1.
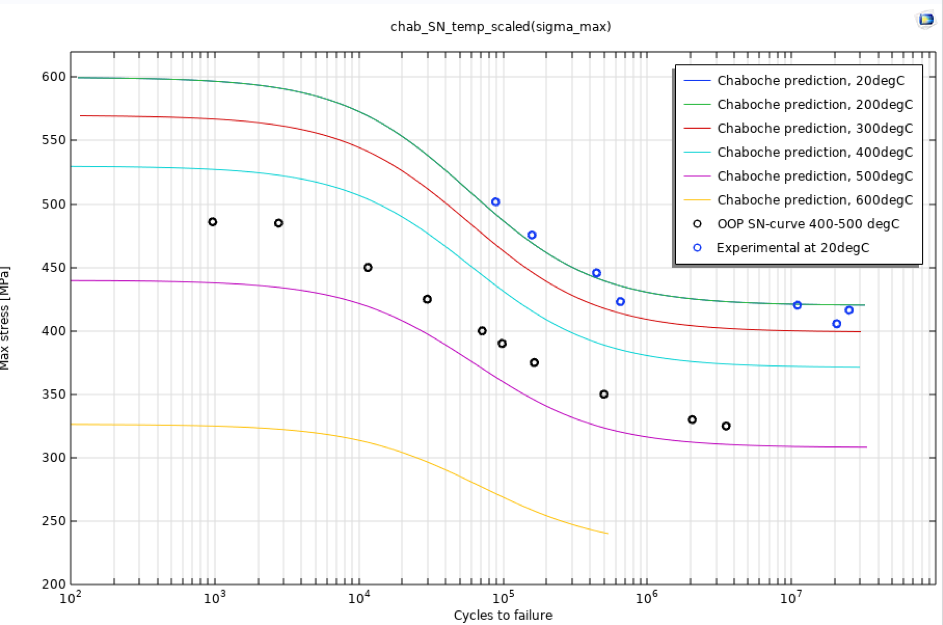
Abbildung 2. S-N-Kurven nach Chaboche mit Temperaturabsenkung.
Die Skalierung dieser Kurven für die Temperatur ist im nächsten Abschnitt dargestellt. Ebenfalls enthalten sind die berechneten Zyklen bis zum Versagen für eine ausgewählte Anzahl von Spannungsniveaus unter der Annahme eines phasenverschobenen Temperaturwechsels zwischen 400°C und 500°C, der durch den Aufbau in Ref. 2 definiert ist.
Wenn der Einfluss der Mittelspannung berücksichtigt werden soll, wird der Parameter b_{fat} benötigt. Falls erforderlich, wird eine Goodman-Reduktion der Ermüdungsgrenze in Bezug auf die mittlere Spannung verwendet, das heißt wenn \bar\sigma=\sigma_u, \sigma_l=0. Daraus ergibt sich b_{fat}=0.0041/MPa.
Computergestützte Modelle
Hintergrund: Experimenteller Vergleich
In Ref. 2 wurden experimentelle thermomechanische Ermüdungsversuche (isotherm und phasenverschoben) durchgeführt. Uniaxiale Zugversuche wurden bei erhöhten Temperaturen und sowohl unter isothermen als auch anisothermen Bedingungen durchgeführt. Zur Veranschaulichung der Festlegung der für eine thermomechanische Ermüdungsanalyse erforderlichen Schritte werden der Versuchsaufbau und das Prüfverfahren in COMSOL Multiphysics® nachgestellt. Die Ergebnisse der publizierten Experimente werden mit den Analyseergebnissen verglichen.
Hintergrund: Ermüdungsauswertung
Um einen realistischeren Fall als einen Probekörper darzustellen, wird eine Ermüdungsanalyse eines Druckbehälters unter zyklischer Temperatur- und Druckbelastung durchgeführt. Die Eingabe für die Ermüdungsberechnung ergibt sich aus dem resultierenden Spannungszustand und die Anzahl der Zyklen bis zum Versagen wird geschätzt.
Geometrisches Modell: Experimenteller Vergleich
In Ref. 2 ist die Geometrie der Probe dargestellt. Für eine einfache Berechnung der zyklischen Spannungs-Dehnungs-Kurven genügt es, nur die Hälfte des schmalen Bereichs als achsensymmetrisches Modell zu modellieren, siehe Abbildung 3. Der Versatz von der axialen Achse ist auf ein Loch im Probekörper zurückzuführen.
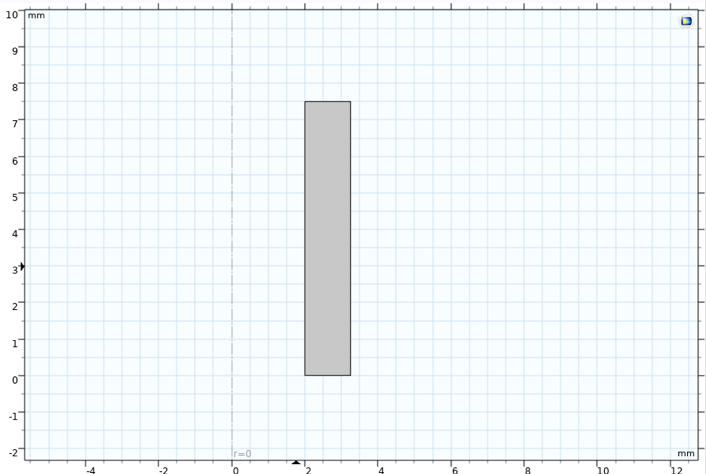
Abbildung 3. Achsensymmetrisches Modell des Prüfkörpers.
Geometrisches Modell: Ermüdungsauswertung
Der Druckbehälter, welcher einen realistischen Fall von thermomechanischer Ermüdung darstellt, hat eine Gesamtlänge von 6000 mm, einen Innenradius von 950 mm und eine Dicke von 50 mm. Er lässt sich leicht als achsensymmetrisches Modell modellieren; siehe Abbildung 4.
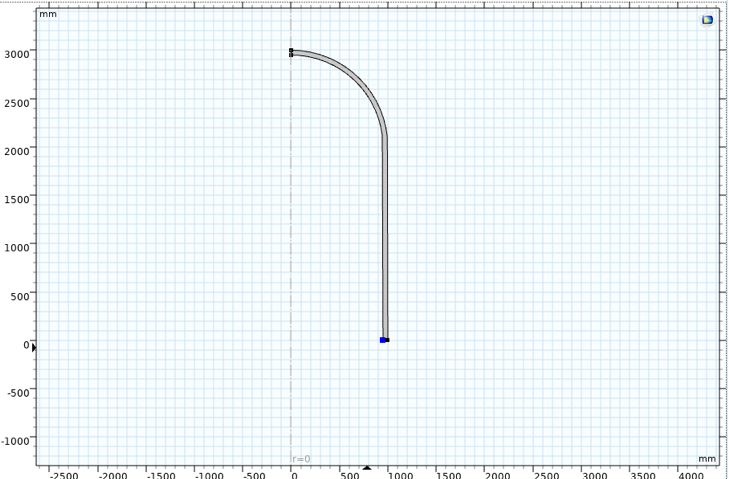
Abbildung 4. Achsensymmetrisches Druckbehältermodell.
Netz: Experimenteller Vergleich
Bei sehr gleichmäßiger Belastung kann das Netz grob sein. In diesem Fall wird ein freies Dreiecksnetz mit einer maximalen Elementgröße von 0,75 mm verwendet, wie in Abbildung 5 dargestellt.
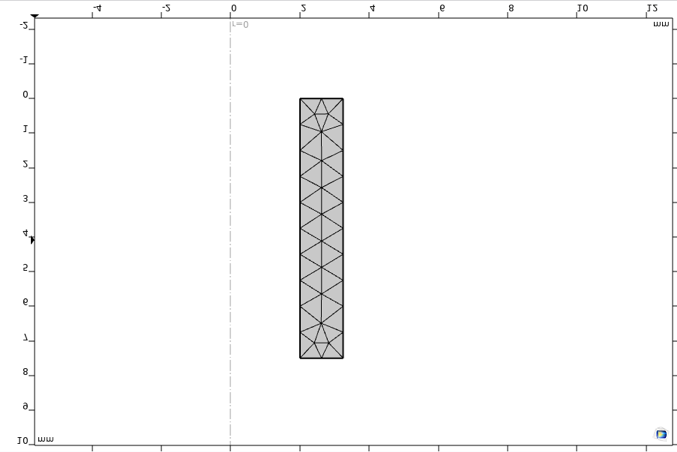
Abbildung 5. Netz des uniaxialen Prüfkörpers.
Netz: Ermüdungsauswertung
Das Modell des Druckbehälters wird mit einem freien Dreiecksnetz mit einer maximalen Maschenweite von 50 mm vernetzt, wie in Abbildung 6 dargestellt. Es wird darauf geachtet, dass immer mehr als ein Element pro Dicke vorhanden ist, obwohl dies für die Demonstration in diesem Blog-Beitrag von geringer Bedeutung ist.
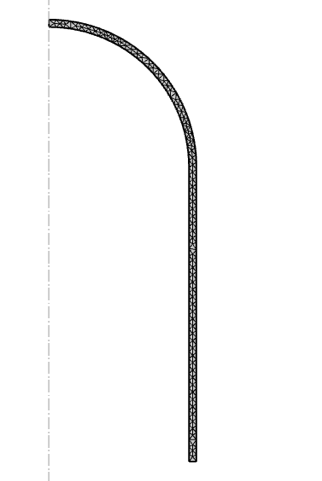
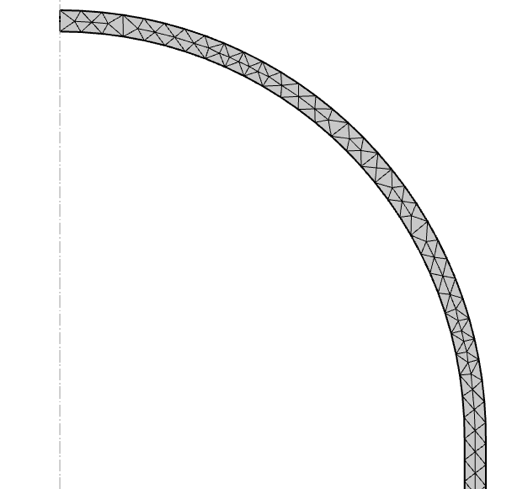
Abbildung 6. Netz für Druckbehälter.
Physik-Einstellungen: Materialien, Belastungen und Randbedingungen (Experimenteller Vergleich)
Für eine thermomechanische Ermüdungsanalyse wird das Interface Solid Mechanics verwendet. Zunächst muss das Material definiert werden. Um die im vorherigen Abschnitt beschriebenen notwendigen Modelle zu ermöglichen, fügen wir die in Abbildung 7 gezeigten Knoten mit Viskoplastizität und Kriechverhalten hinzu.
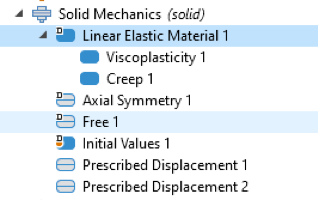
Abbildung 7. Erforderliche Knoten für die Materialdefinition.
Für die linear-elastischen, viskoplastischen und Kriechknoten werden die entsprechenden Materialparameter in ihrer temperaturabhängigen Form eingegeben, wie im nächsten Abschnitt gezeigt wird.
Da das Modell achsensymmetrisch ist, ist nur eine Begrenzung in Achsenrichtung erforderlich. Der untere Rand mit z = 0 wird in Richtung z begrenzt. Der obere Rand hingegen erhält die Verschiebung, die der gemessenen Dehnung für den betreffenden Lastfall entspricht.
Physik-Einstellungen: Materialien, Belastungen, Randbedingungen (Ermüdungsauswertung)
Im Fall des Druckbehälters ist der Materialaufbau identisch. Ebenso wird die Symmetriekante bei z = 0 in Richtung z eingeschränkt. Auf die Innenkante der Wand wird eine Druckbelastung aufgebracht. Diese Druckbelastung ist ein Lastfall von R = 0 mit einem maximalen Druck von 170 bar. Die Temperaturzyklen sind höher als im experimentellen Vergleich, wobei die höchste Temperatur (600°C) bei 0 bar und die niedrigste (500°C) bei 170 bar liegt. Die Belastungsrate beträgt 5,67 bar/s.
Einstellungen der Studie: Experimenteller Vergleich
Für die Verwendung von Kriech- und viskoplastischen Materialmodellen ist eine zeitabhängige Studie erforderlich.
Bei der isothermen Prüfung wird der Anfangszyklus zum Vergleich herangezogen. Bei einer Dehnungsrate von 0,1 %/s beträgt die Anfangszykluszeit 20 s. Die Ausgangszeit wird auf 2,5 s eingestellt. Der Zeitschritt wird manuell auf 0,25 s eingestellt.
Für den anisothermen Fall wird der 50. Zyklus zum Vergleich herangezogen. Bei einer Dehnungsrate von 0,033 %/s beträgt die anfängliche Zykluszeit 60 s und die Gesamtzeit 3000 s. Die Ausgabezeit wird auf 2,5 s und der Zeitschritt auf 1 s eingestellt. Die Temperaturrate beträgt 3,33 °C/s.
Einstellungen der Studie: Ermüdungsauswertung
Bei der Druckbehälteranalyse sind die Last- und Temperaturraten die gleichen wie beim anisothermen experimentellen Vergleich. Die Einstellungen für Ausgabe und Zeitschritt sind ebenfalls identisch.
Funktions- und Variablendefinitionen
Der Aufbau eines Modells, das für die thermomechanische Ermüdungsanalyse geeignet ist, ist an sich nicht allzu komplex, doch der oben dargelegte Rahmen umfasst viele Aspekte. Zunächst wird ein Rahmen für die konsistente Variation der Temperatur und der temperaturabhängigen Materialparameter sowie der Belastung benötigt. In COMSOL Multiphysics® wird dies am einfachsten durch die Verwendung von Funktionen und Variablen erreicht. Dieser Abschnitt beschreibt die Methode anhand der anisothermen Analyse (zum experimentellen Vergleich).
Parameter
Wir beginnen mit der Definition globaler Parameter, die nicht von der Lösung beeinflusst werden, einschließlich Geometrie, Belastung, Materialkriechen und Materialermüdungsparameter (siehe Abbildung 8).
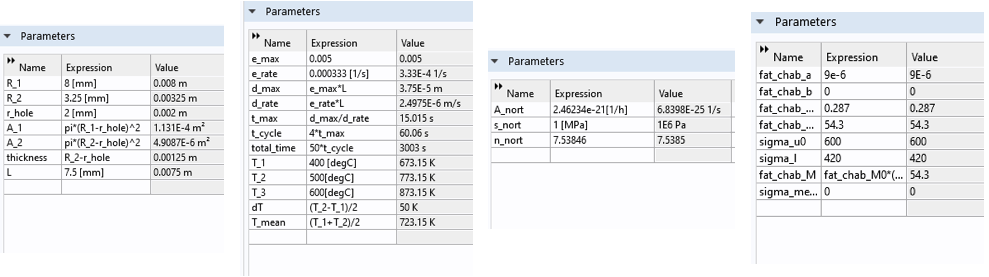
Abbildung 8. Globale Parameter.
Jetzt können die Nennlastwerte (wie Temperaturen und Verschiebungen) durch einfache Skalierungsfunktionen angewendet werden, die die Form der Belastung bestimmen.
Temperaturfunktionen
Beim isothermen Versuch beträgt die Temperatur konstant 400 °C. Der anisotherme Versuch erfordert eine Temperaturdefinition mit maximaler Temperatur (500 °C) bei minimaler Dehnung und minimaler Temperatur (400 °C) bei maximaler Dehnung. Diese Variation wird durch die Erstellung einer Waveform- und einer analytischen Funktion erreicht, wie in Abbildung 9 dargestellt.
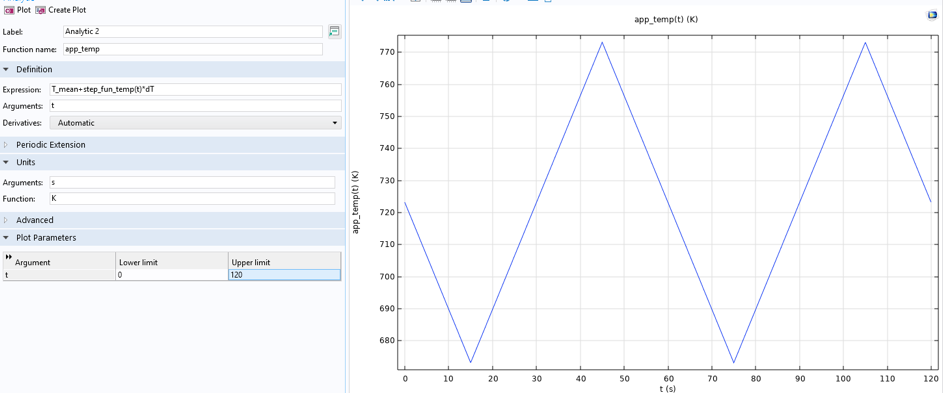
Abbildung 9. Temperaturfunktionen, anisothermer Lastfall.
Die Temperatur wird dann einfach als Variable (TempVar) auf das Modellgebiet angewendet, wie in Abbildung 10 dargestellt.
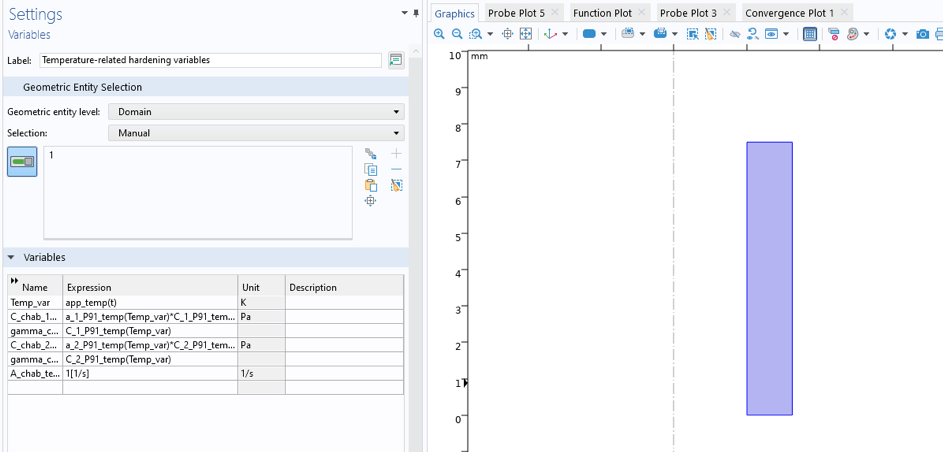
Abbildung 10. Definition der Temperatur als Variable auf dem Gebiet.
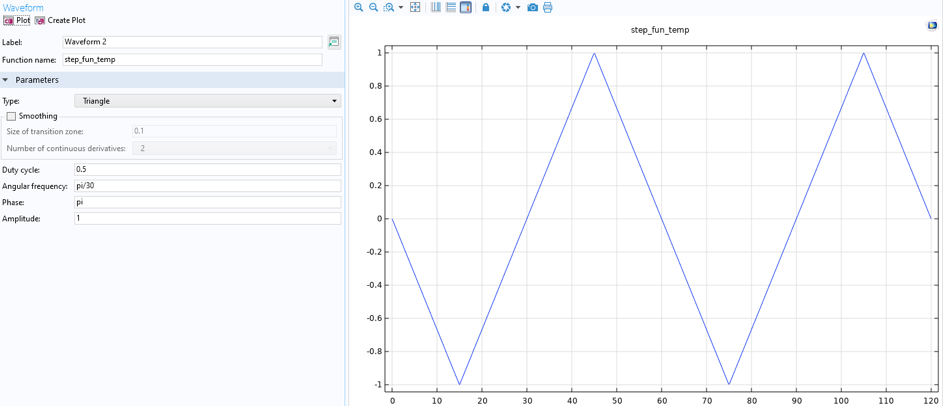
Für den Druckbehälter ändert sich die Temperatur zyklisch zwischen 500 °C und 600 °C, wie in Abbildung 11 dargestellt. Die Temperatur wird ebenfalls als Gebietsvariable im Modell dargestellt.
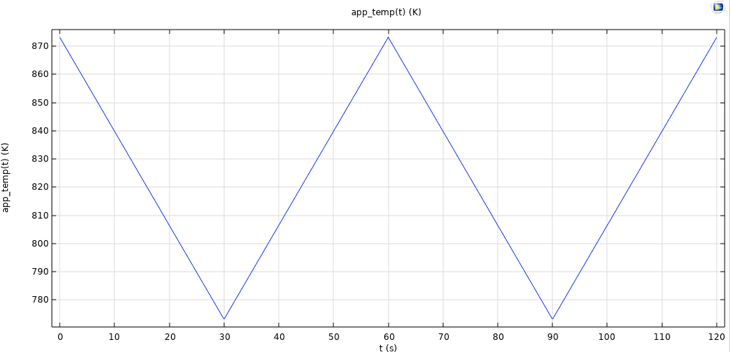
Abbildung 11. Temperaturfunktion, Druckbehälter.
Die eingeführte Temperaturvariable kann zur Bestimmung der Variation der Materialeigenschaften verwendet werden, berücksichtigt jedoch nicht die thermische Expansion. Dies ist im experimentellen Fall von geringer Bedeutung, da die Gesamtdehnung (mechanisch und thermisch) maschinengesteuert ist, aber im Allgemeinen sollte die thermische Dehnung aufgrund der thermischen Expansion berücksichtigt werden. Zu diesem Zweck kann ein physikalisches Interface Heat Transfer in Solids integriert und eine punktuelle Einschränkung hinzugefügt werden, um die gewünschte Temperatur zu erhalten, wie in Abbildung 12 dargestellt.
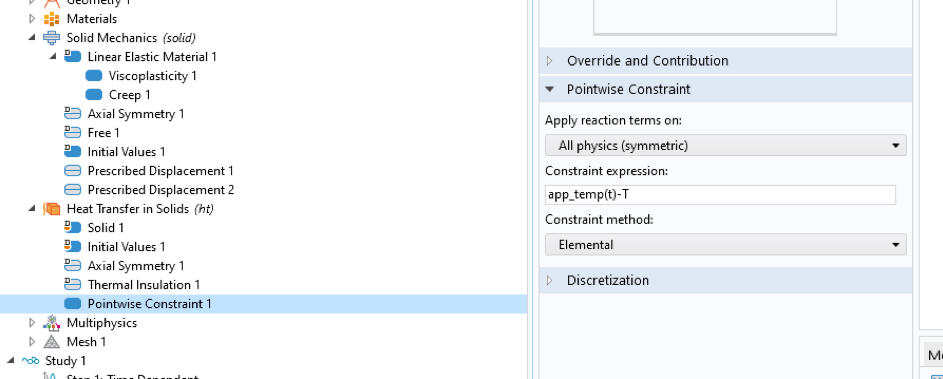
Abbildung 12. Das physikalische Interface Heat Transfer in Solids.
Natürlich ist eine homogene Temperaturverteilung selten realistisch. Eine richtige Wärmetransportanalyse kann auch zur Ermittlung des Temperaturfeldes verwendet werden. Dazu muss eine Referenztemperatur festgelegt werden. Dies ist die Temperatur, bei der die thermischen Spannungen gleich Null sind, also eine (thermisch) spannungsfreie Konfiguration. Während dies normalerweise bei Raumtemperatur der Fall ist, sind für die Ermüdungsanalyse in der Regel der Lastbereich und der Mittelwert von Bedeutung. Daher wird die Referenztemperatur in der Analyse auf 873 K, die maximale Temperatur des Zyklus, festgelegt.
Lastfunktionen
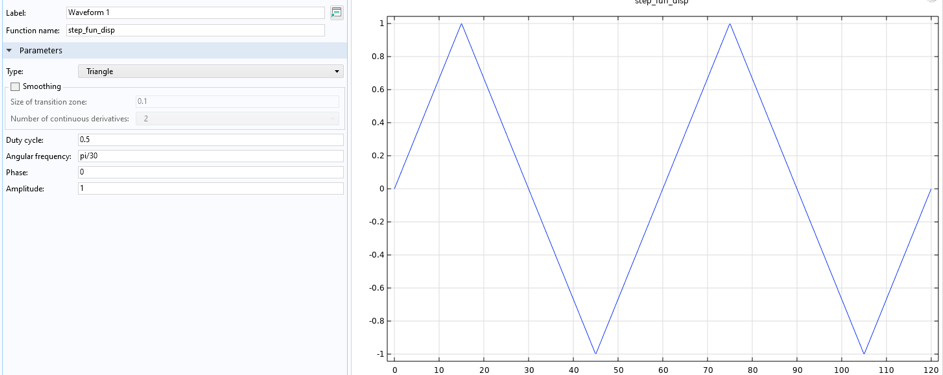
Ähnlich wie bei der Temperaturdefinition wird auch die Last (in diesem experimentellen Fall eine Verschiebung) durch zwei separate Funktionen definiert: die Waveform- und die analytische Funktion (siehe Abbildung 13).
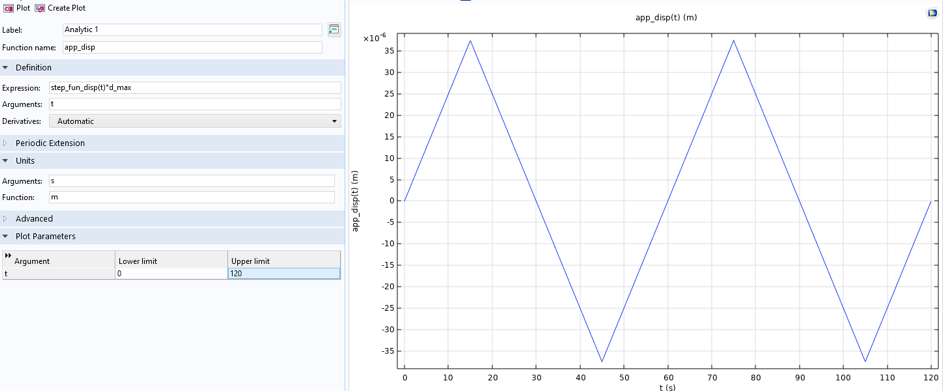
Abbildung 13. Lastfunktionen, anisothermer Lastfall.
Diese Abbildung gilt speziell für den anisothermen Versuchsfall. Die Dehnungsraten unterscheiden sich zwischen dem anisothermen und dem isothermen Fall. Im isothermen Fall beträgt die Dehnungsrate 0,1 %/s und im anisothermen Fall 0,033 %/s, was Verschiebungsraten von 7,5 µm/s bzw. 2,5 µm/s entspricht. Die maximale Dehnung während der Zyklen beträgt 0,5 %, was einer Gesamtverschiebung von 37,5 µm entspricht. Dies hängt mit der Messlänge von 7,5 mm zusammen, bei der die Dehnung über den schmalen Bereich der Probe gemessen wird. Hierbei wird ein Modell mit halber Länge verwendet; die volle Länge des schmalen Bereichs beträgt 15 mm.
Im Fall des Druckbehälters wird eine Lastfunktion mit einem Spitzendruck von 170 bar und einer Lastrate von 5,67 bar/s definiert, wie in Abbildung 14 dargestellt.
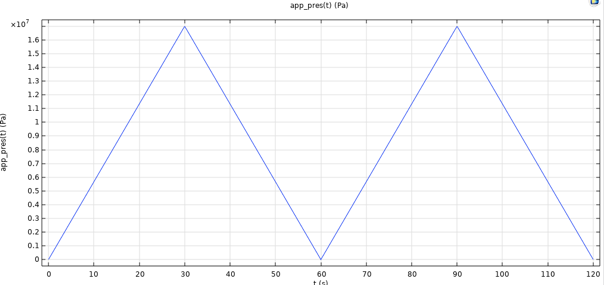
Abbildung 14. Lastfunktion, Druckbehälter.
Materialparameter-Funktionen
Die Materialparameter müssen eine Temperaturabhängigkeit aufweisen, was am einfachsten durch die Erstellung einer Interpolationsfunktion mit bekannten Parameterwerten bei bestimmten Temperaturen erreicht wird. Beispielsweise ist σsat wie in Abbildung 15 definiert.
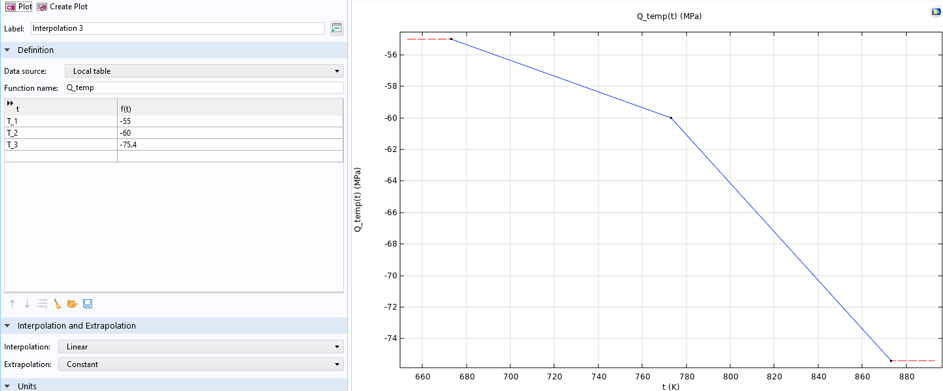
Abbildung 15. Definition der Funktion für die temperaturabhängige σsat.
Der temperaturabhängige Materialparameter wird dann durch Aufruf dieser Funktion unter Verwendung der erzeugten Temperaturvariablen als Argument richtig berechnet. Abbildung 16 zeigt dies beispielhaft für den obigen Parameter, vgl. Abbildung 9. Natürlich kann auch die abhängige Variable T aus dem Physik-Interface Heat Transfer in Solids als Argument verwendet werden.
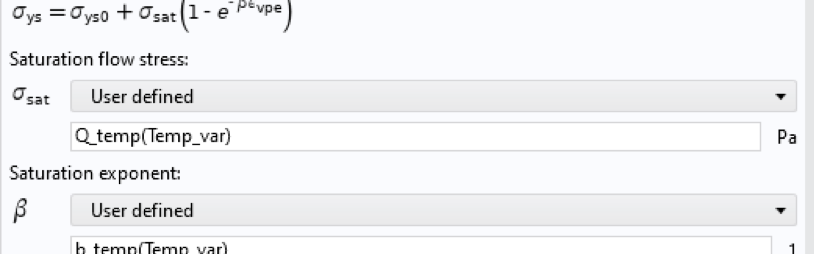
Abbildung 16. Aufruf der Temperaturvariablen in der Definition des Materialparameters.
Die Skalierung der Zugfestigkeit und der Ermüdungsgrenze mit der Temperatur erfolgt ähnlich wie oben beschrieben, wobei ein Referenzwert bei Raumtemperatur dann mit einem dimensionslosen Reduktionsfaktor skaliert wird (da sowohl die Zugfestigkeit als auch die Dauerfestigkeit skaliert werden müssen). Der Ausdruck der analytischen Funktion, die die S-N-Kurve nach Chaboche definiert (siehe Abbildung 1 und Abbildung 2), ist in Abbildung 17 dargestellt, wobei die Funktion bei Raumtemperatur (293 K) als Funktion der maximalen Spannung definiert ist.

Abbildung 17. Analytische Funktion für die S-N-Kurve von Chaboche.
Die Skalierungsfunktion UTS_temp_scaling ist wie in Abbildung 18 definiert.
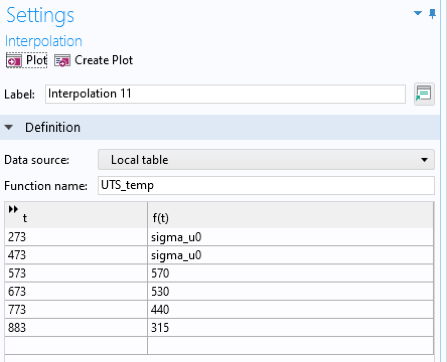
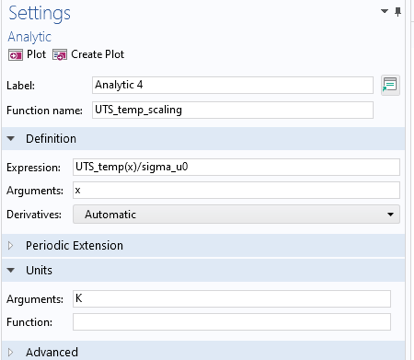
Abbildung 18. Skalierungsfunktion für die Zugfestigkeit.
Ergebnisse: Experimenteller Vergleich
Am oberen Ende des Modells, wo die Verschiebung vorgegeben ist, wurde eine Randsonde für den Mittelwert der ersten Piola-Kirchhoff-Spannung erstellt. Diese wurde extrahiert und als Funktion der angewandten Dehnung geplottet, um zyklische Spannungs-Dehnungs-Kurven zu erhalten.
Isotherme Prüfung
Die anfängliche zyklische Spannungs-Dehnungs-Kurve ist in Abbildung 19 dargestellt.
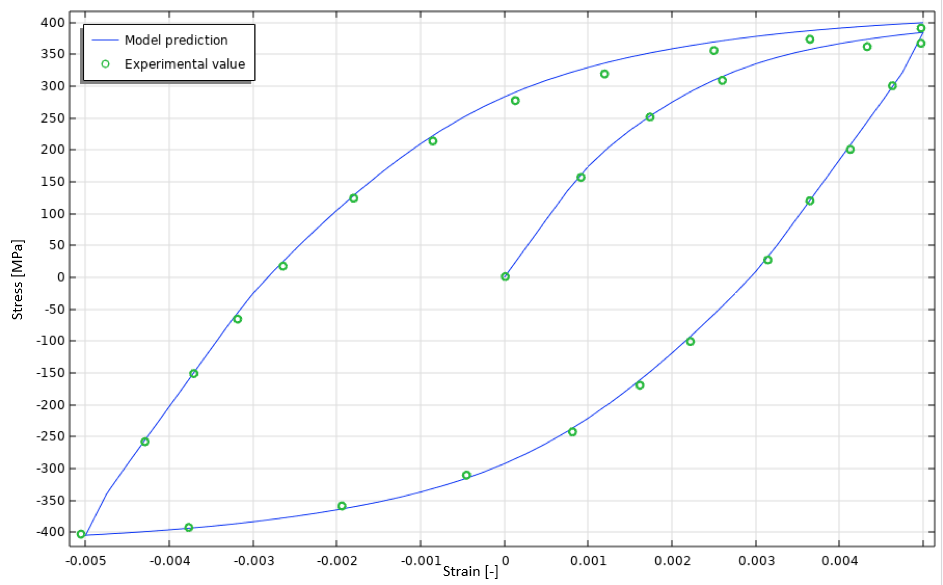
Abbildung 19. Anfängliche zyklische Spannungs-Dehnungs-Kurve, isothermer Fall.
Wie erwartet scheint das Modell die anfängliche zyklische Spannungs-Dehnungs-Kurve gut vorherzusagen.
Anisotherme Prüfung
Die anisothermen zyklischen Spannungs-Dehnungs-Kurven sind in Abbildung 20 zu sehen.
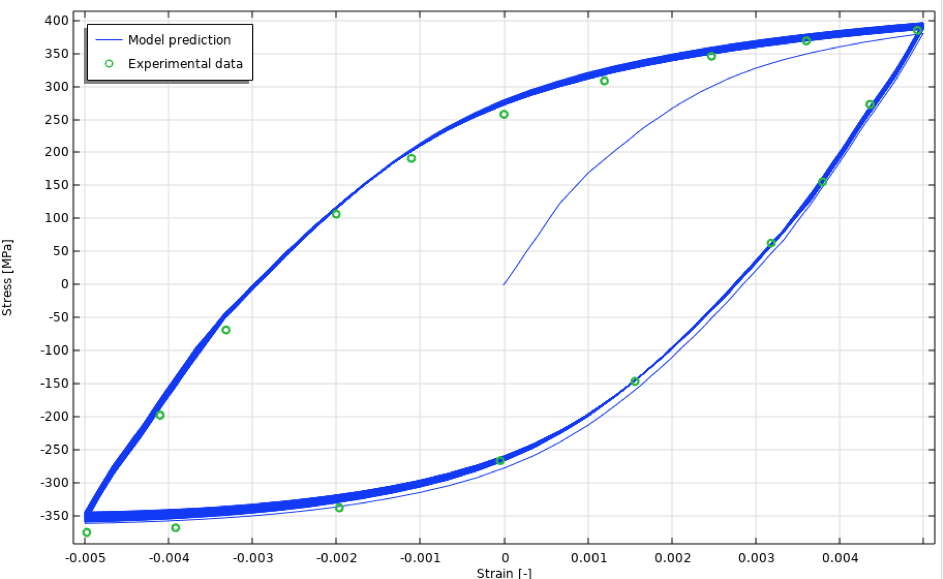
Abbildung 20. Zyklische Spannungs-Dehnungs-Kurven, anisothermer Fall.
Die isolierte Spannungs-Dehnungs-Kurve des 50. Zyklus ist in Abbildung 21 dargestellt.
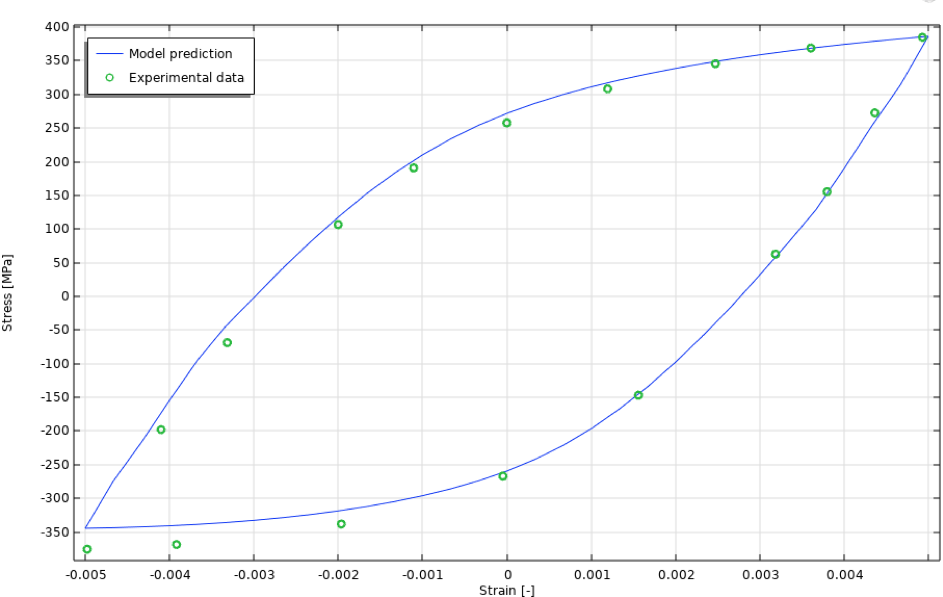
Abbildung 21. 50. zyklische Spannungs-Dehnungs-Kurve, anisothermer Fall.
Ergebnisse: Ermüdungsauswertung
Spannungen und Dehnungen
Die Von-Mises-Spannung bei maximaler Belastung (2970 s) und nach Entlastung (3000 s) des 50. Zyklus ist in Abbildung 22 dargestellt.
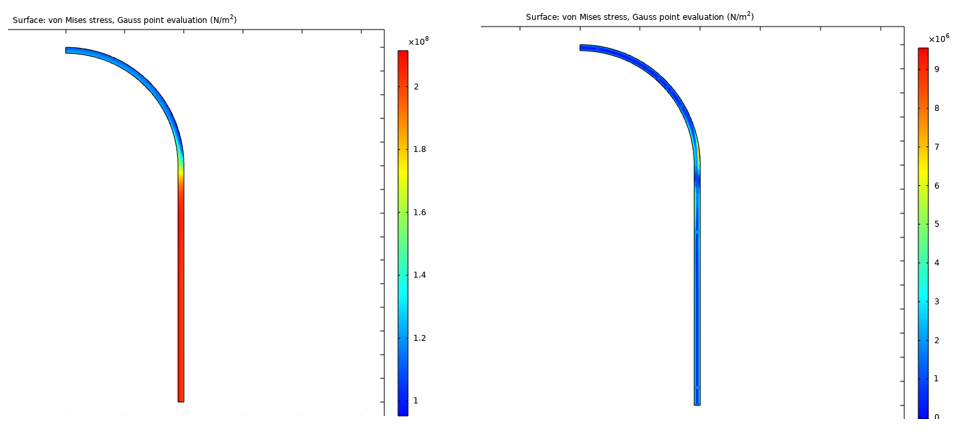
Abbildung 22. Von-Mises-Spannung bei maximaler Belastung (links) und nach Entlastung (rechts) des 50. Zyklus.
Die äquivalente viskoplastische und die Kriechdehnung nach dem 50. Zyklus ist in Abbildung 23 dargestellt.
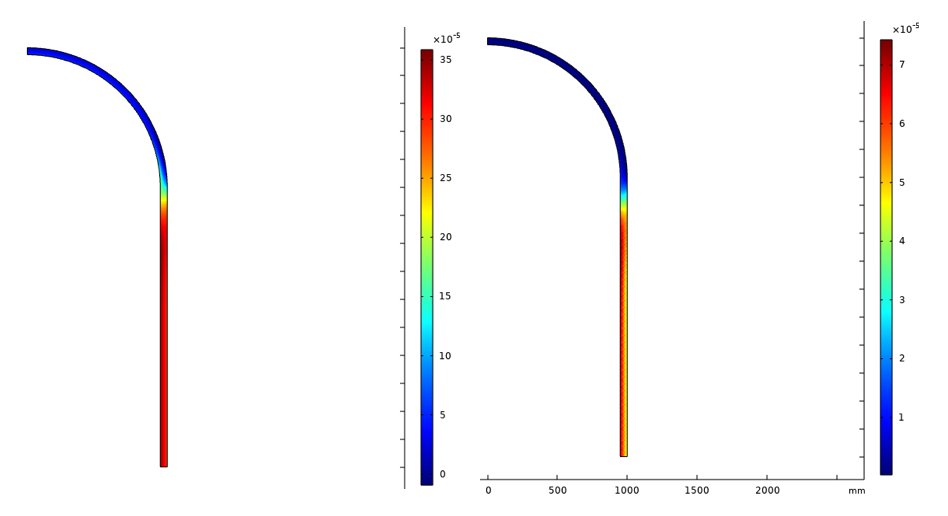
Abbildung 23. Äquivalente viskoplastische (links) und Kriechdehnung (rechts) nach dem 50. Zyklus.
Ein typisches Verhalten unsymmetrischer Spannungszyklen ist das Ratcheting, bei dem die Restdehnung mit jedem Zyklus zunimmt. Das nichtlineare kinematische Verfestigungsmodell berücksichtigt dies. In der Regel neigen Belastungszyklen mit hoher mittlerer Spannung dazu, die Ratcheting-Dehnung zu erhöhen, während eine niedrigere mittlere Spannung die Ratcheting-Dehnung im Laufe der Zeit stabilisiert. Um die Anzahl der Ermüdungszyklen abzuschätzen, ohne jeden Zyklus bis zum Versagen berechnen zu müssen (siehe nächster Abschnitt), ist ein stabilisierter Spannungs-Dehnungs-Zyklus erforderlich. Abbildung 24 zeigt schematisch mit einem Plot der maximalen Von-Mises-Spannung für die maximale äquivalente deviatorische Dehnung im Druckbehälter die Ratcheting-Dehnung für zwei Extremfälle.
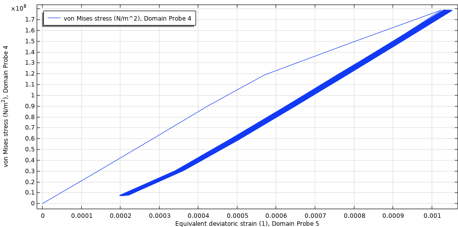
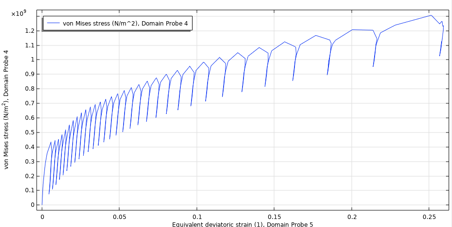
Abbildung 24. Ratcheting-Dehnung bei niedriger mittlerer Spannung und maximalem Druck 100 bar (links) sowie bei hoher mittlerer Spannung und maximalem Druck 240 bar (rechts). In beiden Fällen handelt es sich um eine Belastung von R = 0.
Bei der niedrigen mittleren Spannung stabilisiert sich der Zyklus fast sofort. Im Fall der hohen mittleren Spannung nimmt die Ratcheting-Dehnung mit jedem Zyklus zu. Für den hier betrachteten Lastfall mit einem maximalen Druck von 170 bar ist das Ratcheting-Verhalten der ersten 50 Zyklen in Abbildung 25 dargestellt, die an der unteren rechten Ecke des Modells entnommen wurde. Zur Sicherheit können auch die Maximalwerte des Gebiets entnommen werden.
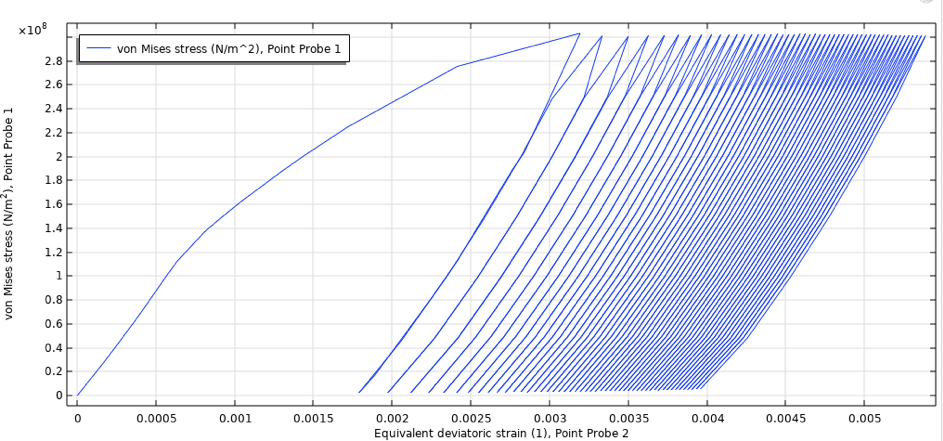
Abbildung 25. Spannungs-Dehnungs-Verhalten für den Druckbehälter, 170 bar maximaler Druck, gegenphasiges Zyklieren zwischen 500 °C und 600 °C.
Die Ratcheting-Dehnung nimmt mit jedem Zyklus deutlich ab; die Spannungs-Dehnungs-Kurve kann nach 50 Zyklen als stabilisiert betrachtet werden.
Berechnete Zyklen bis zum Versagen
Es gibt mehrere Möglichkeiten, die Ermüdungslebensdauer eines Bauteils mit Hilfe der in den vorhergehenden Abschnitten definierten Gleichungen abzuschätzen. Die akkumulierte Schädigung kann für jeden Zyklus berechnet werden, indem zunächst die effektive Temperatur T* bestimmt wird, so dass
Der Schadensverlauf für einen Zyklus kann dann berechnet werden gemäß
Der Gesamtschaden ergibt sich dann aus der Summe der Schäden für jeden Zyklus. Wenn es sich um repräsentative Lastzyklen handelt, kann die Anzahl solcher Sequenzen bis zum Versagen (D = 1) bestimmt werden. Es ist auch möglich, den Schaden für jeden Zyklus einfach zu berechnen und zu summieren und die Analyse bis D = 1 durchzuführen. Da diese Ansätze einen Rahmen für die Definition und Bewertung der für jeden Zyklus berechneten Variablen erfordern, können sie aufwändig sein. Außerdem erfordert die Analyse einer Komponente bis zum Versagen in der Regel die Berechnung von einigen hundert bis hin zu tausenden Zyklen, selbst bei Ermüdung mit niedrigen Zyklen. Bei großen Modellen ist dies normalerweise nicht praktikabel.
Wenn das Bauteil jedoch nur einer Art von Last-/Temperaturzyklus ausgesetzt ist, wie in diesem Blog-Beitrag, kann die Anzahl der Zyklen bis zum Versagen analytisch berechnet werden als
Anschließend muss nur noch die mittlere und maximale Spannung für einen stabilisierten Zyklus berechnet und der obige Ausdruck ausgewertet werden. Zunächst sollte der Spannungs-Dehnungs-Plot für ermüdungsgefährdete Punkte im Laufe der Zeit visualisiert werden, um einen stabilisierten Zyklus zu gewährleisten. Gemäß Abbildung 25 scheint der Spannungs-Dehnungs-Zyklus stabilisiert zu sein.
Die mittlere Spannung wird als abgeleiteter Wert eines Operators für den Mittelwert über ein Zeitintervall von einer Punktlösungssonde für die maximale Spannung gemäß Abbildung 26 berechnet: 149,7 MPa.
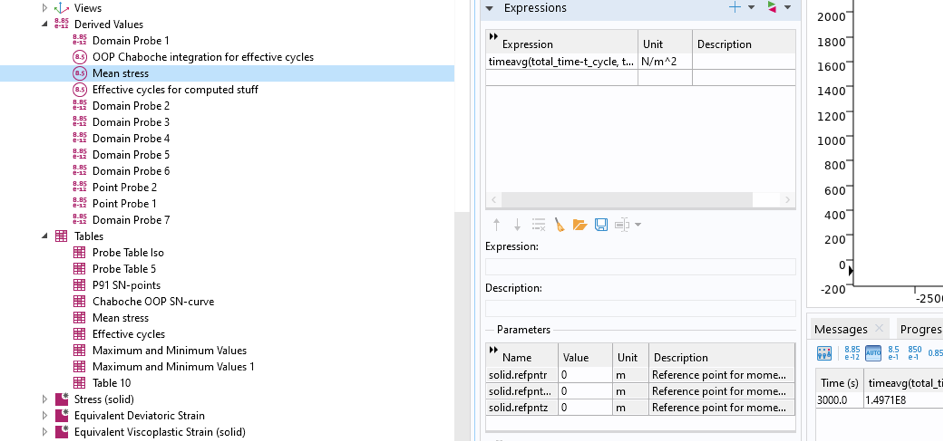
Abbildung 26. Berechnung der mittleren Spannung für einen stabilisierten Zyklus.
Der analytische Ausdruck für die Anzahl der Zyklen N_{F}^{*} ist als Funktion der Zeit, der maximalen und der mittleren Spannung gemäß Abbildung 27 definiert. Dieser Ausdruck unterscheidet sich vom allgemeinen Ausdruck in Abbildung 17, da er in einem Zeitintegral verwendet werden muss.

Abbildung 27. Definition für eine berechnete Anzahl von Zyklen bis zum Versagen als Funktion der Zeit, der maximalen und der mittleren Spannung.
Dies wird zur Berechnung der Anzahl der Zyklen bis zum Versagen als abgeleiteter Wert verwendet, wie in Abbildung 28 dargestellt. Die maximale Spannung kann am einfachsten aus der Sondentabelle ermittelt werden: 313 MPa.
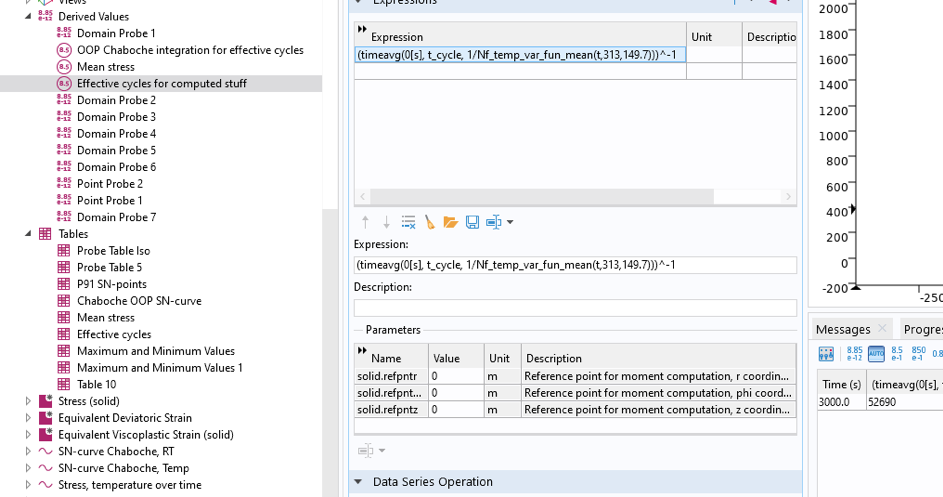
Abbildung 28. Berechnung der Anzahl der Zyklen bis zum Versagen mithilfe des Knotens Global Evaluation.
Die berechnete Anzahl der Zyklen bis zum Versagen beträgt 52.690.
Schlussfolgerungen und Diskussion
Die thermomechanische Ermüdung ist in vielen Anwendungsbereichen von großer Bedeutung, wie etwa bei Kraftwerken, die zur Verringerung der Emissionen mit immer höheren Temperaturen betrieben werden. Bei hohen Temperaturen und hohen Belastungen beeinflussen temperaturabhängige Materialeigenschaften, Kriechen und thermische Dehnungen die thermomechanische Ermüdung.
Mit COMSOL Multiphysics® können diese Phänomene durch die Verwendung der in diesem Blog-Beitrag beschriebenen nichtlinearen Materialmodelle einbezogen werden. Von besonderer Bedeutung sind dabei die Verfestigungsparameter, die das zeitliche Verhalten der zyklischen Spannungs-Dehnungs-Kurve bestimmen. Durch die Möglichkeit, benutzerdefinierte Funktionen für die Temperatur zu definieren und dann die Materialeigenschaften temperaturabhängig zu machen, kann das bekannte Ermüdungsmodell von Chaboche verwendet werden, um die Anzahl der Zyklen bis zum Ermüdungsversagen eines Bauteils abzuschätzen, das gleichzeitig thermischer und mechanischer Belastung ausgesetzt ist. Dies ist mit analytischen Ausdrücken leicht möglich, wenn der Last-/Temperaturzyklus während der gesamten Lebensdauer des Bauteils gleich ist.
Für eine komplexere Belastungshistorie müsste für jeden Zyklus eine effektive Temperatur bestimmt werden, die für die thermische und mechanische Belastung in diesem Zyklus repräsentativ ist. Diese würde dann verwendet, um die relevanten Materialparameter (in diesem Blog-Beitrag die Zugfestigkeit und die Ermüdungslebensdauer), die in der Funktion f(\sigma_M, \bar\sigma, D, T^*) verwendet werden, richtig zu skalieren und den Schaden für diesen bestimmten Zyklus zu berechnen. Bei diesem inkrementellen Verfahren würde sich der Schaden akkumulieren, und wenn D = 1 ist, wird angenommen, dass ein Ermüdungsversagen eintritt. Wenn jedoch die Anzahl der Zyklen einige tausend übersteigt, ist dieser Ansatz wegen des hohen Zeitaufwands nicht praktikabel. Wenn möglich, sollte eine Abfolge repräsentativer Zyklen (ein Lastblock) bestimmt werden.
In diesem Zusammenhang sind einige Aspekte zu berücksichtigen. Das im genannten Artikel verwendete Materialmodell basiert auf einem vereinheitlichten viskoplastischen Modell nach Chaboche, bei dem die viskose Spannung in Abhängigkeit von denselben Materialparametern, die auch im viskoplastischen Verfestigungsmodell nach Chaboche verwendet werden, in die Lösung eingeht. Das vereinheitlichte viskoplastische Modell ist in COMSOL Multiphysics® nicht implementiert; stattdessen wird in diesem Blog-Beitrag das Kriechgesetz von Norton verwendet. Die mit COMSOL Multiphysics berechneten Ergebnisse stimmen dennoch gut mit den experimentellen Daten überein. Auch die Verwendung der Von-Mises-Spannung als Ermüdungsspannung ist aufgrund ihrer Unabhängigkeit von hydrostatischen Belastungen aus technischer Sicht möglicherweise keine gute Wahl. Das Sines-Kriterium könnte beispielsweise besser geeignet sein, da die Belastung proportional ist und die Richtung der Hauptspannungsrichtungen als konstant angenommen werden kann. Die Implementierung des Sines-Kriteriums bringt in diesem Blog-Beitrag jedoch nur wenige Vorteile.
Über den Autor
Björn Fallqvist ist Consultant bei Lightness by Design und arbeitet an der Produktentwicklung auf der Grundlage numerischer Analysen. Er hat 2016 am Royal Institute of Technology promoviert und sich mit der Entwicklung von konstitutiven Modellen zur Erfassung des mechanischen Verhaltens biologischer Zellen befasst. Sein berufliches Hauptinteresse und seine Spezialisierung liegen im Bereich der Materialcharakterisierung und der Anwendung verschiedener Materialmodelle zur Erfassung physikalischer Phänomene.
Referenzen
- S. Natesan et al., Preliminary Materials Selection Issues for. s.l. : Argonne National Laboratory, 2006.
- C.J. Hyde et al., “Thermo-mechanical fatigue testing and simulation using a viscoplasticity model for a P91 steel”, Computational materials science, no. 56, 2012.
- J.L. Chaboche and P.M. Lesne, “A non-linear continuous fatigue damage model”, Fatigue fracture and Engineering Materials Structures, vol. 11, no. 1, pp. 1&ndash17, 1987.
- A.A. Saad et al., “Thermal-mechanical fatigue simulation of a P91 steel in a temperature range of 400-600C”, Materials at high temperatures, no. 28, 2011.
- COMSOL Multiphysics, Structural Mechanics Module User’s Guide.
- X. Feng et al., “Determination of creep properties of P91 by small punch testing”, Materials at high temperatures, vol. 32, no. 4, 2015.
- Y. Gorash and D. MacKenzie, Open Eng, vol. 7, 2017.



Kommentare (0)