Waren Sie schon einmal in der Situation, dass Sie experimentelle Daten als Last- oder Randbedingung verwenden wollten? Wenn diese Daten räumlich oder zeitlich variieren und verrauscht sind, benötigen Sie möglicherweise ein sehr feines Netz oder der Löser erfordert sehr kurze Zeitschritte, was wir in der Praxis oft nicht wollen oder brauchen. Eine mögliche Lösung besteht darin, die Eingabedaten zu filtern, um sie glatter zu machen. Finden wir mehr heraus!
Filtern verrauschter Daten mit gleichungsbasierter Modellierung
Sehen wir uns als Beispiel einige Eingabedaten an, die in der folgenden Abbildung dargestellt sind. Wir wollen uns zunächst nicht damit befassen, was diese Daten darstellen, sondern stellen uns vor, dass die horizontale Achse entweder den Raum oder die Zeit repräsentieren könnte. Wir können feststellen, dass die Daten sowohl erhebliches Rauschen als auch erkennbare Trends aufweisen. Bevor wir die Daten in unserem Modell verwenden, wollen wir dieses Rauschen reduzieren.
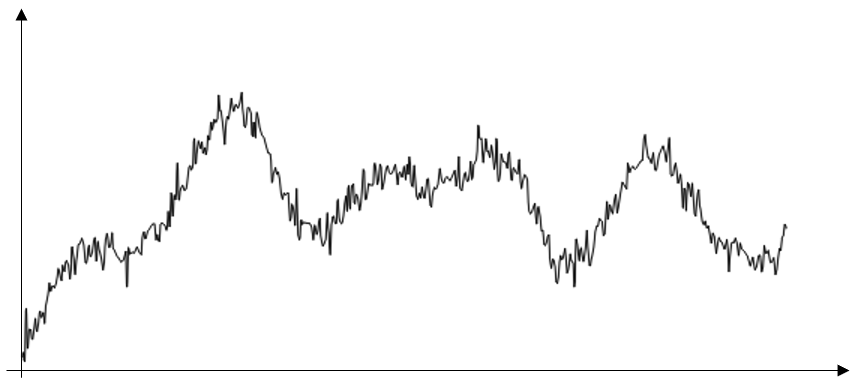
Stichprobe von Daten mit erheblichem Rauschen.
Wir können hier einen sogenannten Helmholtz-Filter verwenden. Diese Art von Filter wurde kürzlich vorgeschlagen und hat sich im Bereich der Topologieoptimierung als sehr nützlich erwiesen. Tatsächlich ist diese Funktion ein eingebautes Feature des Optimization Module, aber sie kann auch manuell implementiert werden, was wir hier tun werden.
Der Helmholtz-Filter löst einfach die maßgebliche partielle Differentialgleichung:
wobei D die Eingabedaten und u die gefilterten Daten sind.
Es gibt einen Parameter in dieser Gleichung, R, den wir den Filterradius nennen werden.
Neben der maßgeblichen Gleichung benötigen wir auch Randbedingungen. Aus Gründen, die weiter unten erläutert werden, beginnen wir mit der homogenen Neumann-Bedingung, was bedeutet, dass der Gradient der Felder an den Rändern gleich Null ist. Um diese Gleichung zusammen mit dieser Randbedingung zu lösen, werden wir die gleichungsbasierte Modellierung durch das Interface Coefficient Form PDE in einer 1D-Komponente verwenden.
Zunächst lesen wir unsere experimentellen Daten in ein Tabellen-Feature Interpolation ein, wie im folgenden Screenshot gezeigt. Beachten Sie, dass die Extrapolation auf Constant eingestellt ist. Wie wir gleich sehen werden, benötigen wir aufgrund der Randbedingungen in unserem Helmholtz-Filter einige Daten für den Pufferbereich von Raum oder Zeit außerhalb unseres Interessenbereichs.
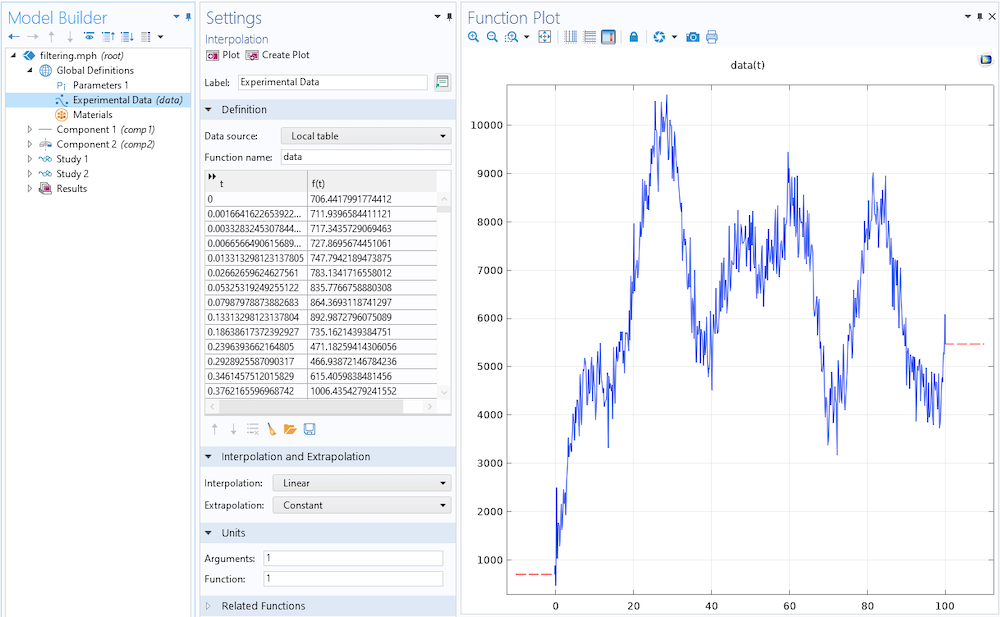
Einlesen der experimentellen Daten und Einstellen der Extrapolationsmethode.
Als nächstes fügen wir unserem Modell eine 1D Componenthinzu und setzen das Unit System auf None.
Dann erstellen wir ein Feature Interval in Geometry, wie im Screenshot unten gezeigt. Beachten Sie die zusätzlichen Regionen an den Seiten des interessanten Datenbereichs.
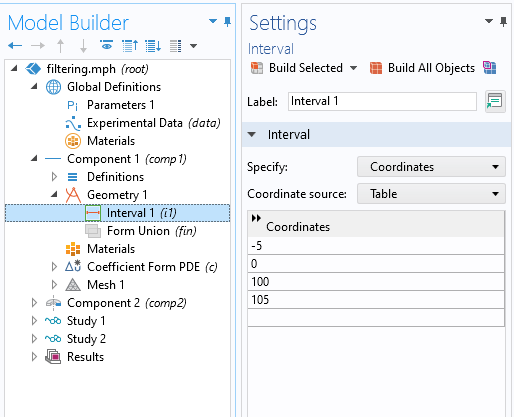
Festlegen des Gebiets, auf das der Filter angewendet wird.
Nun führen wir ein Interface Coefficient Form PDE in Component ein, und zwar in Form einer einzigen Unbekannten, u, wie im Screenshot unten gezeigt. Wir belassen Discretization bei der Standardeinstellung Lagrange Quadratic. Auch hier lassen wir alles dimensionslos.
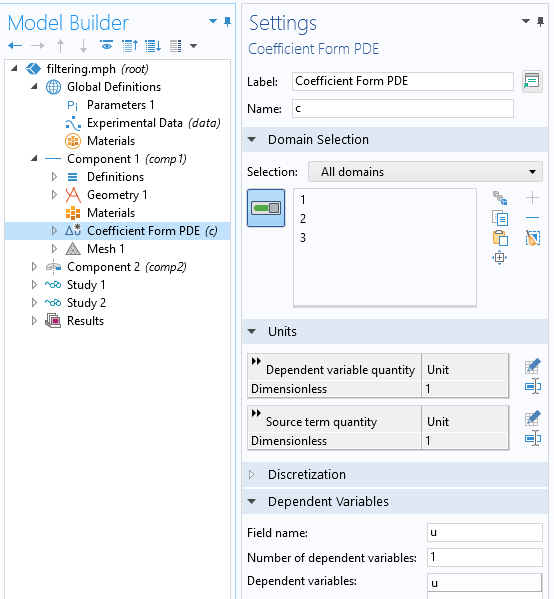
In den Einstellungen für das Feature Coefficient Form PDE legen wir die Einstellungen wie unten gezeigt fest. Der Diffusion Coefficient wird auf das Quadrat des globalen Parameters FilterSize gesetzt und der Absorption Coefficient ist 1. Die Quelle ist unser experimenteller Datensatz und alle anderen Terme werden auf Null gesetzt.
Die Standard-Randbedingung Zero Flux ist die gewünschte homogene Neumann-Bedingung, und wir werden die Ableitung unseres gefilterten Datensatzes so festlegen, dass sie an den Enden des Rechengebiets Null ist. Dies führt zu einem Endeffekt des Filters, weshalb wir die Geometrie und die Daten mit einem zusätzlichen Füllbereich versehen haben.
Wir könnten alternativ die Randbedingung Dirichlet verwenden, die den Wert von u am Rand festlegt. Außerdem müssen wir die Größe des Netzes manuell so einstellen, dass sie kleiner ist als die Auflösung unserer experimentellen Daten.
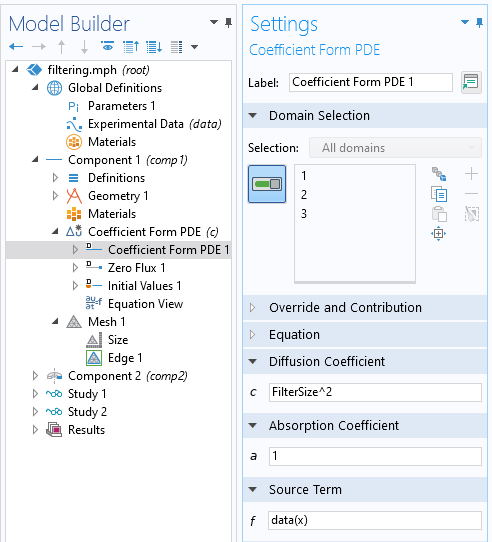
Verwendung der gleichungsbasierten Modellierung zur Definition der Helmholtz-Filtergleichung.
Verwendung der Helmholtz-Filtergleichung für Modelldaten
Wir können nun verschiedene Werte für die Filtergröße berechnen und die Ergebnisse vergleichen. Wie wir unten sehen, hat eine sehr kleine Filtergröße fast keinen Effekt. Größere Filtergrößen führen zu einer stärkeren Glättung, und je größer der Filterradius wird, desto mehr nähern sich die gefilterten Daten dem Durchschnitt des Originals an.
Es ist wichtig, diese Schlüsseleigenschaft des Helmholtz-Filters zu erkennen: Er ist energieerhaltend, solange die homogenen Neumann-Randbedingungen verwendet werden. Das bedeutet, dass das Integral der Originaldaten und der gefilterten Daten über das gesamte Rechengebiet dasselbe ist.
Es ist zu beachten, dass dies nicht genau für das Teilgebiet ohne die Pufferzonen an beiden Enden gilt. Es ist auch wichtig zu bedenken, dass die Randbedingung Dirichlet nicht energieerhaltend ist und daher mit Vorsicht verwendet werden sollte.

Beispiele für gefilterte Daten mit verschiedenen Filterradien.
Nachdem wir die Daten gefiltert haben, können wir sie nun in einem Modell verwenden. Wir werden die transiente Erwärmung eines achsensymmetrischen 2D-Materialstücks betrachten, und die gefilterten Daten werden die auf die exponierten Oberflächen wirkende Wärmebelastung darstellen. Da sich unser Wärmemodell in einer anderen Komponente innerhalb unseres Modells befinden wird, müssen wir eine Möglichkeit einführen, unsere Daten aus unserer 1D-Komponente in die Zeitdimension zu verschieben, um sie in einer achsensymmetrischen 2D-Komponente zu verwenden. Dies geschieht über den Operator General Extrusion, wo wir eine Destination Map für den x-Ausdruck von t definieren. Mit diesem Feature werden die Daten aus der 1D-Komponente auf die Zeitachse abgebildet bzw. extrudiert und damit überall im Modell allgemein verfügbar gemacht.
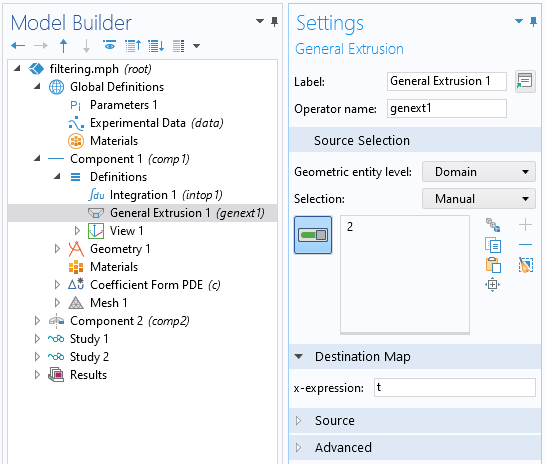
Der Screenshot zeigt die Einstellungen des Operators General Extrusion.
Innerhalb des thermischen Modells in der achsensymmetrischen 2D-Komponente können wir eine Wärmequelle anwenden, wie in der Abbildung unten mit der Wärmelast comp1.genext1(u)[W/m^2] gezeigt. Beachten Sie, dass wir Einheiten hinzufügen, da u dimensionslos ist.
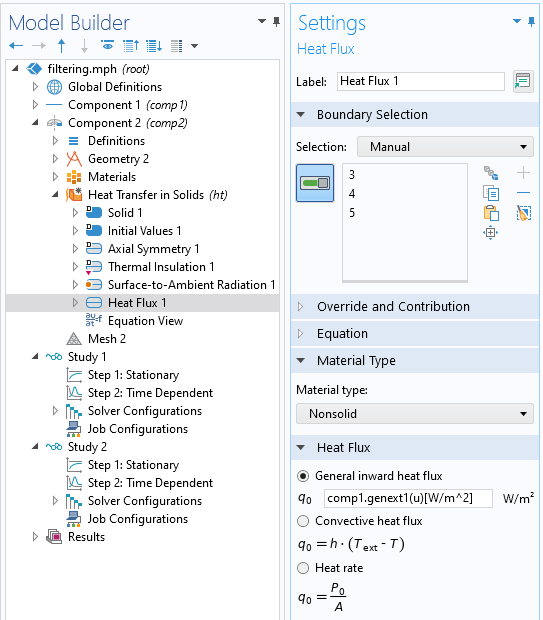
Aufruf der in Component 1 definierten gefilterten Daten aus dem thermischen Modell in Component 2.
Wir können unsere Studie so modifizieren, dass sie zwei Schritte enthält. Der erste ist ein stationärer Schritt, in dem die Filtergleichung gelöst wird, und der zweite ist ein zeitabhängiger Schritt, in dem das thermische Problem gelöst wird. Wir lösen mit einer engeren relativen Toleranz von 1e-4 und geben die Ergebnisse für alle Zeitschritte des Lösers aus, wie in diesem Eintrag der Knowledge Base beschrieben.
Nebenbei bemerkt: Wenn die Daten stattdessen deutliche, scharfe Änderungen in der Größenordnung ohne Rauschen aufweisen, sollten Sie alternativ das Interface Events verwenden, um die Informationen dem Löser zugänglich zu machen.
Durch Lösen für verschiedene Werte des Filterradius und durch den Plot der Spitzentemperatur innerhalb des Gebiets über die Zeit können wir die Auswirkungen der Filterung auf die thermische Lösung erkennen. Wir sehen, dass es in diesem Fall nur eine sehr geringe Auswirkung auf die Spitzentemperatur im Laufe der Zeit gibt.
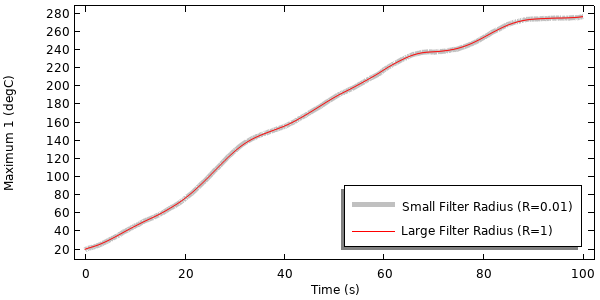
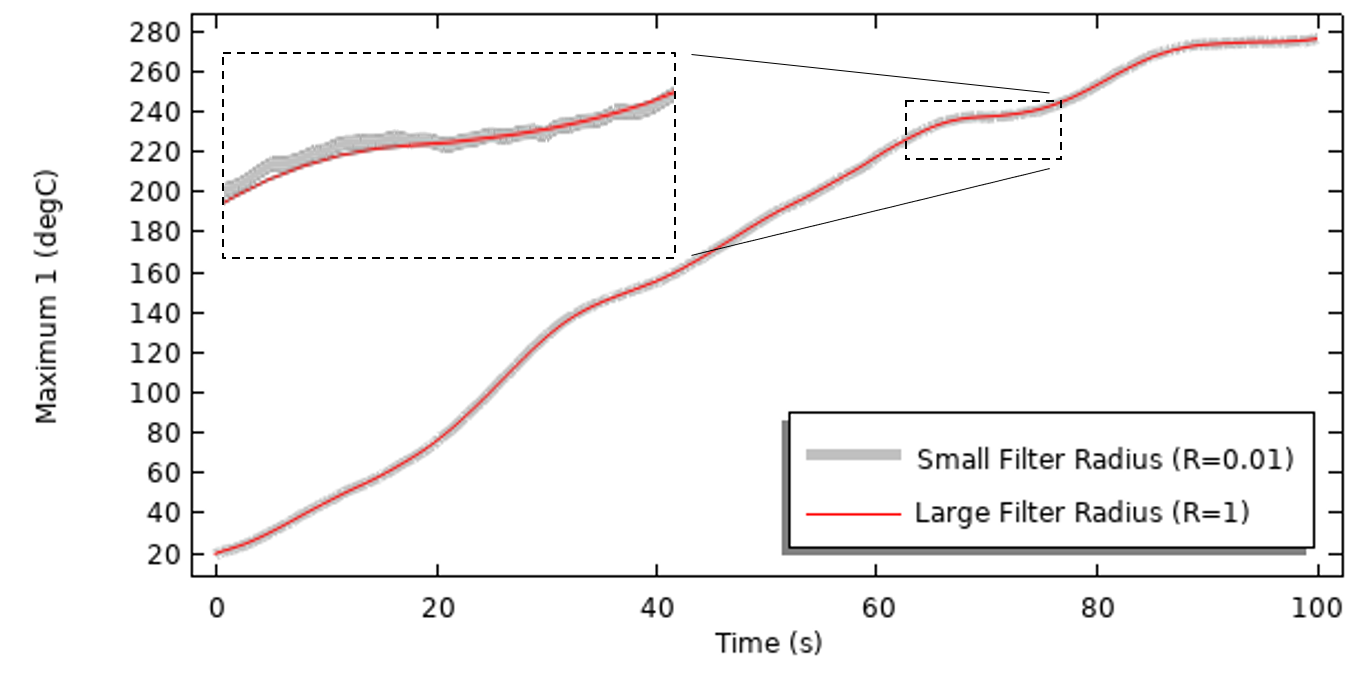
Ergebnisse des thermischen Modells, das mit verschiedenen Filtern für die instationäre Wärmelast gelöst wurde.
Der dramatische Unterschied liegt hier in der Lösungszeit. Die Lösung eines Modells ohne Filterung erfordert insgesamt etwa 700 adaptive Zeitschritte, während die Lösung des Modells mit einer moderaten Filtergröße etwa 130 Zeitschritte erfordert, was zu einer mehr als fünffachen Verbesserung der Lösungszeit führt!
Abschließende Überlegungen
Hier haben wir gezeigt, wie eine zusätzliche Komponente und Gleichung verwendet werden kann, um einen Helmholtz-Filter auf Daten anzuwenden, die wir in unser Modell eingeben wollen. Wir können dies nicht nur mit 1D-Daten, sondern auch mit 2D- oder 3D-Daten tun, und wir können diesen Filter über jede beliebige geometrische Form und mit jeder beliebigen Dichte der Eingabedaten implementieren. Vor allem in 2D und 3D übertrifft diese Methode die meisten anderen Filtertechniken, da sie die lokale kompakte Unterstützung der Finite-Elemente-Basisfunktionen ausnutzt und eine ungleichmäßige räumliche Netzdiskretisierung ermöglicht. Dies führt zu spärlichen linearen Matrizen, die sehr effizient gelöst werden können.
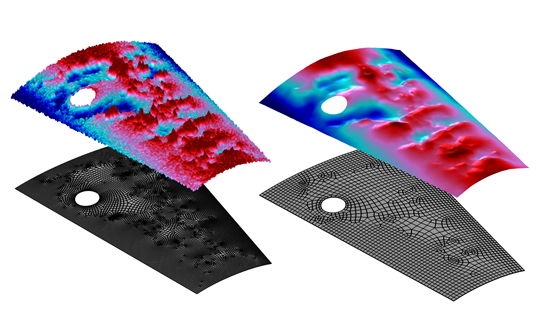
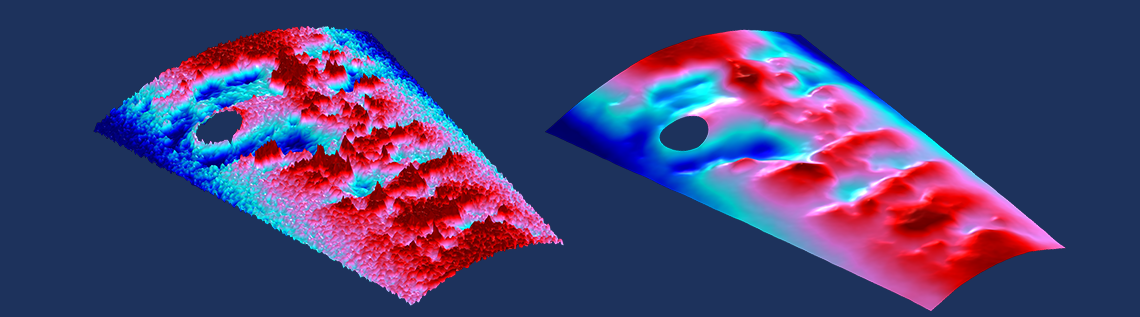
Räumliche Filterung mit einem Helmholtz-Filter auf einer beliebigen Fläche. Die gefilterten Daten können mit einem gröberen Netz gut repräsentiert werden.
Ein Beispiel für die 2D-Glättung ist in der obigen Abbildung von ungefilterten und gefilterten Feldern über einer beliebigen Fläche zu sehen. Beachten Sie, dass die Filterung der Daten die Lösung eines Modells, das diese Daten verwendet, auf einem relativ gröberen Netz ermöglichen würde, was uns einen zusätzlichen Rechenvorteil verschafft. Es stellt sich heraus, dass wir diesen Helmholtz-Filter sogar verwenden können, um ein Netz zu entwerfen, das sich gut an die Variationen in unseren Eingabedaten anpasst, aber das ist ein Thema für ein andermal!
Versuchen Sie es selbst
Die zu diesen Ansätzen gehörenden Dateien stehen hier zum Download bereit:



Kommentare (0)