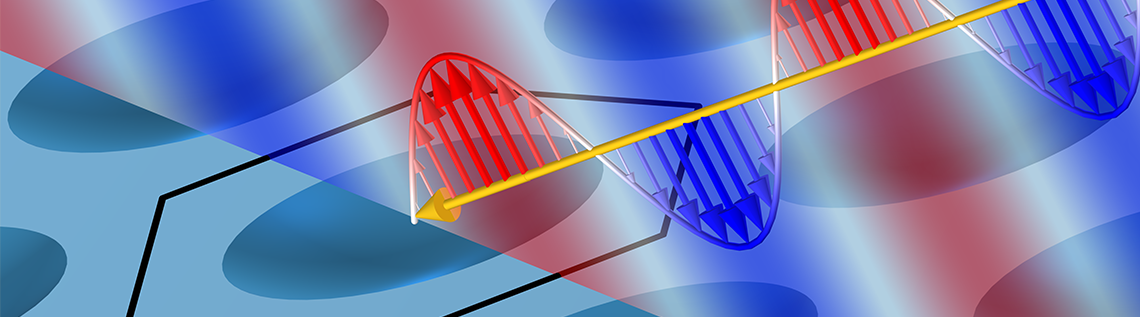
Wenn eine ebene Welle elektromagnetischer Strahlung, wie zum Beispiel Licht, auf eine ebene periodische Struktur trifft, kann es zu einer Beugung höherer Ordnung kommen. Das bedeutet, dass das Licht nicht nur gemäß dem Snelliusschen Brechungsgesetz reflektiert und gebrochen wird, sondern auch in mehrere verschiedene Richtungen gestreut werden kann, die als Beugungsordnungen bezeichnet werden. Ein geometrischer Ansatz kann uns helfen zu verstehen, wann diese vorhanden sind und in welche Richtungen das Licht gestreut wird.
Beugung an planaren periodischen Strukturen
Wir betrachten hier eine ebene Lichtwelle, die auf eine Struktur trifft, die in einer Ebene unendlich periodisch ist. Die Medien oberhalb und unterhalb der Ebene können unterschiedliche Brechungsindizes haben und werden als verlustfrei und von unendlicher Ausdehnung angenommen. In der Ebene der Grenzfläche zwischen diesen Medien können periodische Strukturen beliebiger Komplexität in Bezug auf Materialeigenschaften und Form auftreten, solange sich diese in der Ebene periodisch wiederholen. Licht, das auf eine solche Struktur fällt, erfährt zumindest eine spiegelnde Reflexion; das Licht kann auch eine Brechung (auch spiegelnde Transmission genannt) und oft auch einen gewissen Verlust erfahren, da die elektromagnetische Energie in Wärme umgewandelt wird. Die Reflexions- und Brechungswinkel sind durch das Snelliussche Brechungsgesetz gegeben. Die Berechnung des Anteils des einfallenden Lichts, der innerhalb der periodischen Struktur reflektiert, transmittiert oder dissipiert wird, erfordert jedoch eine numerische Analyse.
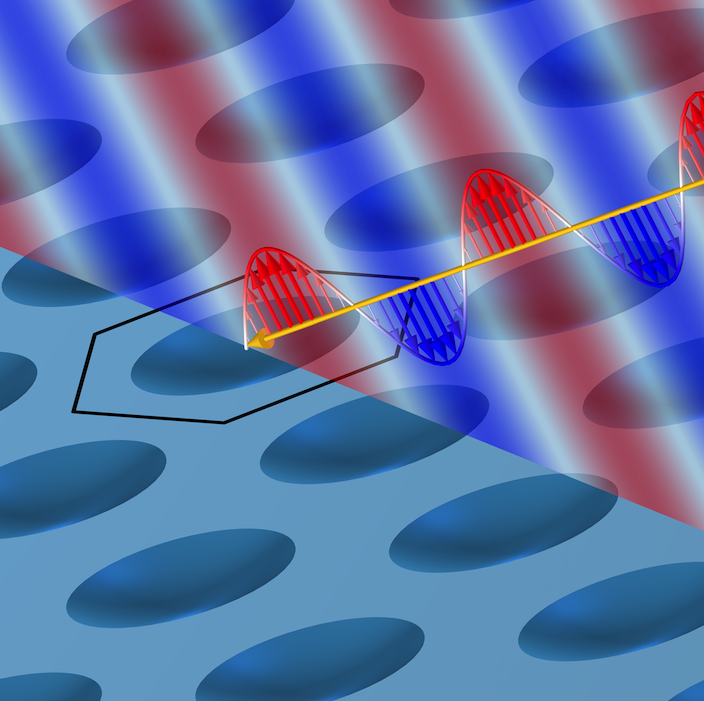
Eine ebene Welle, die unter einem Winkel auf eine planare periodische Struktur trifft. Eine Einheitszelle der periodischen Struktur ist hervorgehoben.
Wie bereits erwähnt, gibt es auch die Möglichkeit der Beugung höherer Ordnung. Dies geschieht, wenn das Licht, das von der periodischen Struktur gestreut wird, konstruktiv in verschiedene Richtungen interferiert. Ein Beispiel für ein solches Ergebnis ist unten abgebildet.
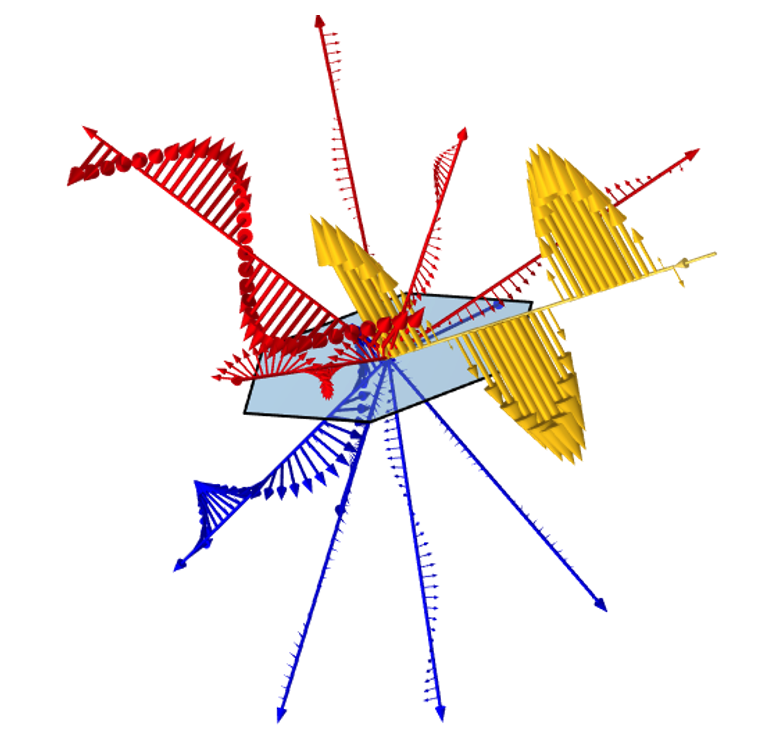
Illustration einer linear polarisierten ebenen Welle (gelb), die auf eine periodische Einheitszelle trifft. Das einfallende Licht wird in mehrere verschiedene Beugungsordnungen mit unterschiedlichen Intensitäten und Polarisationen in Reflexion (rot) und Transmission (blau) gestreut.
Die Bestimmung des Anteils des Lichts, der in diese anderen Richtungen geht, erfordert ebenfalls die Erstellung eines numerischen Modells. Um zu verstehen, in welche Richtungen das Licht gestreut wird, kann jedoch ein rein geometrischer Ansatz verwendet werden, die sogenannte Ewald-Konstruktion. Es ist hilfreich, mit diesem Ansatz vertraut zu sein, bevor Sie mit der numerischen Analyse beginnen, daher stellen wir ihn in diesem Blog-Beitrag vor. Die geometrische Konstruktion der Ewald-Kugel kann sowohl für planare Strukturen mit Periodizität in einer Richtung als auch für solche mit Periodizität in zwei Richtungen in der Ebene verwendet werden.
Strukturen mit Periodizität in einer Richtung
Einige planare periodische Strukturen, wie beispielsweise Gitter, weisen eine periodische Variation in nur einer Richtung auf, d.h. es gibt keine Variation in der Struktur entlang der dritten Dimension. Wenn sich das einfallende Licht in der Ebene senkrecht zu dieser dritten Dimension ausbreitet, kann die Modellierung auf eine zweidimensionale Ebene mit Periodizität entlang einer Richtung reduziert werden.
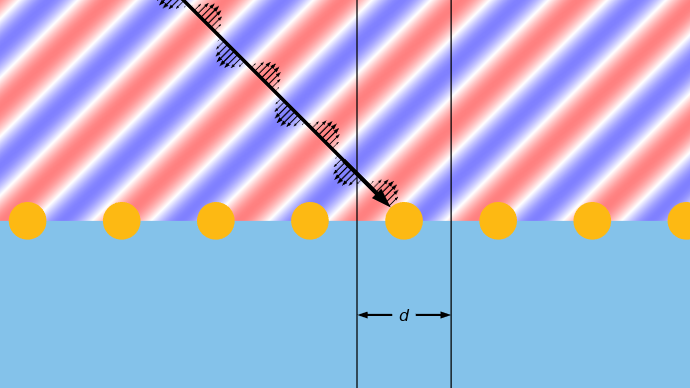
Eine ebene Welle, die in einem Winkel auf eine Struktur mit Periodizität in einer Richtung einfällt, ohne Veränderung der Struktur oder der Felder entlang der Richtung außerhalb der Ebene. Eine Einheitszelle ist hervorgehoben.
Für diese Strukturen müssen wir nur die Abstände der Einheitszellen d berücksichtigen und beginnen mit dem Zeichnen einer Reihe von Gitterpunkten in einem reziproken Raum, daher haben die Dimensionen in der folgenden Abbildung Einheiten der inversen Länge. Die Linie dieser Gitterpunkte entspricht der Ebene der Grenzfläche der periodischen Struktur. Der Abstand zwischen den Gitterpunkten ist 2\pi/d, und die Punkte sind ausgehend von dem nullten Gitterpunkt m=0 indiziert, der sozusagen in der Mitte der Einheitszelle sitzt. Als nächstes werden zwei Halbkreise oberhalb und unterhalb der Linie der Gitterpunkte gezeichnet. Diese haben einen Radius von n_{r}2\pi/\lambda_{0} auf der Reflexionsseite und n_{t}2\pi/\lambda_{0} auf der Transmissionsseite, wobei n_{r} und n_{t} die Refraktionsindizes auf der jeweiligen Seite sind und \lambda_{0} die Wellenlänge im freien Raum ist. Für einfallendes Licht mit einem Winkel von \theta_{inc} von der Normalen, ist der gemeinsame Mittelpunkt dieser Kreise um den nullten Gitterpunkt um sin(\theta_{inc})n_{r}2\pi/\lambda_{0} versetzt. Die Gitterpunkte, die innerhalb dieser Halbkreise liegen, entsprechen den möglichen Beugungsordnungen.
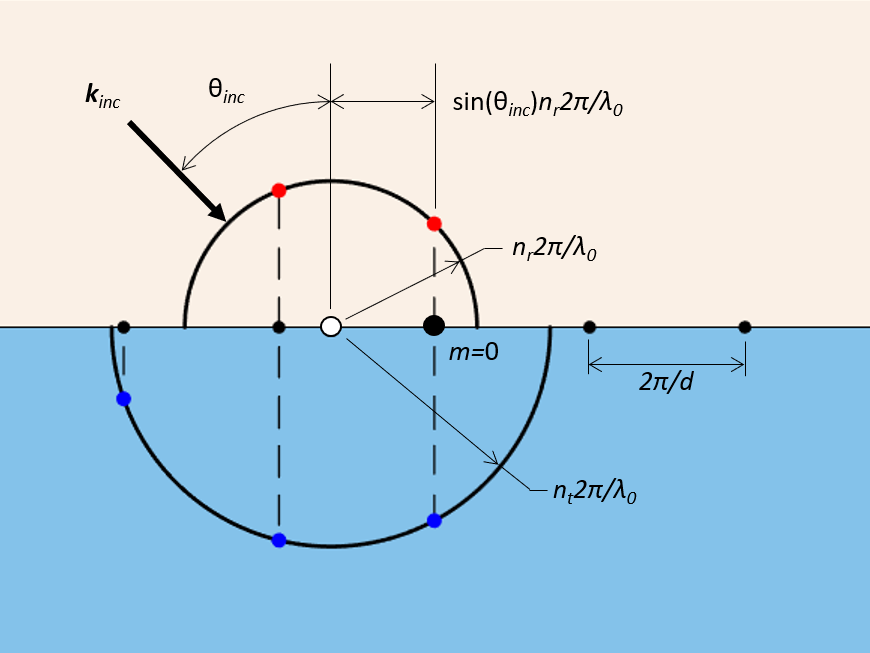
Die geometrische Konstruktion zur Bestimmung der Beugungsordnungen einer planaren Struktur mit Periodizität in einer Richtung, die von einer schräg einfallenden, ebenen Welle beleuchtet wird. Beachten Sie, wie der Mittelpunkt der Halbkreise (weißer Punkt) vom nullten Gitterpunkt versetzt ist.
Diese Konstruktion kann auch verwendet werden, um die Richtungen zu bestimmen, in die die Beugung erfolgt, und jeder eine Indizierung zuzuweisen. Die Vektoren vom Mittelpunkt der Halbkreise zur Projektion der Gitterpunkte entsprechen den \textbf{k}-Vektoren der jeweiligen Beugungsordnung. Die Indizierung dieser Gitterpunkte hat auf beiden Seiten ein entgegengesetztes Vorzeichen. Die Pfeile zu den nullten Gitterpunkten sind immer vorhanden; sie stehen für spiegelnde Reflexion und Transmission. Das Vorhandensein anderer Beugungsordnungen hängt von der Wellenlänge, den Brechungsindizes, den Abständen und dem Einfallswinkel ab. Zwei Beispiele für die Einrichtung eines solchen Modells finden Sie in der Application Gallery: Plasmonic Wire Grating (RF), das das RF Module verwendet, und Plasmonic Wire Grating (Wave Optics), das das Wave Optics Module verwendet.
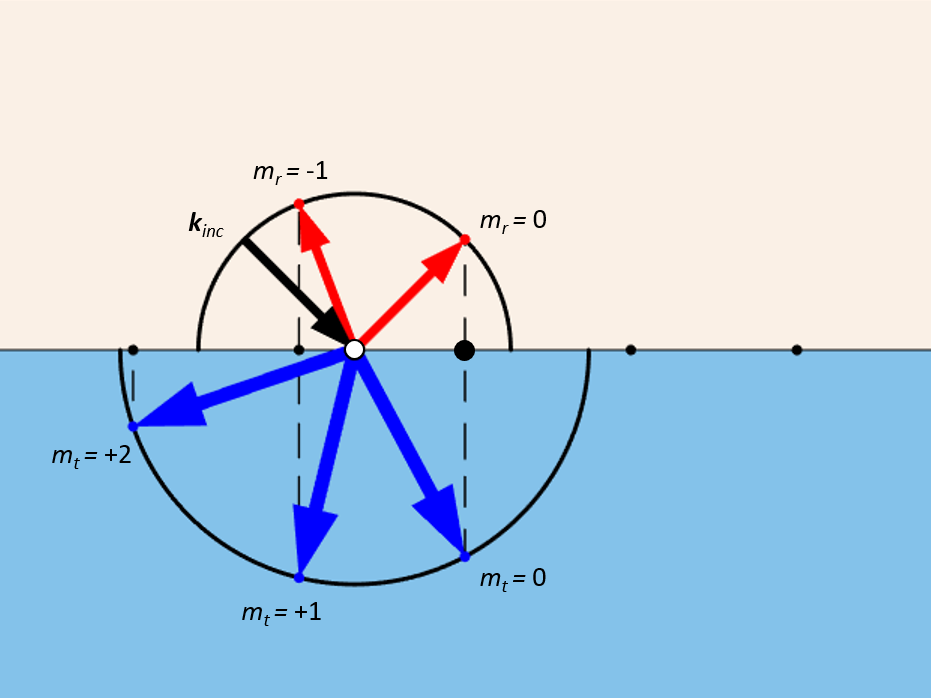
Die Wellenvektoren der verschiedenen Beugungsordnungen von einer planaren Struktur mit Periodizität in einer Richtung. Beachten Sie den Wechsel des Vorzeichens der Indizierung zwischen der Reflexions- und der Transmissionsbeugungsordnung.
Strukturen mit Periodizität in zwei Richtungen
Sehen wir uns jetzt den Fall der Beugung an einer ebenen Struktur mit Periodizität in zwei Richtungen in der Ebene an. Die untenstehende Abbildung zeigt rechteckige, rhomboidische und sechseckige Einheitszellen, die eine Ebene strukturieren. Diese werden durch zwei Einheitszellenvektoren definiert, \textbf{a}_{1} und \textbf{a}_{2}, die an einem Punkt beginnen und den angrenzenden Kanten bis zum nächsten Scheitelpunkt folgen. Obwohl wir mit beliebigen Koordinaten und Orientierungen arbeiten können, werden wir für die Zwecke dieses Blog-Beitrags den Vektor \textbf{a}_{1} so wählen, dass er an der globalen kartesischen x-Achse ausgerichtet ist und aus der Beleuchtungsrichtung immer nach unten auf die Einheitszelle schaut. Es gibt auch zwei Basisvektoren, \textbf{b}_{1} und \textbf{b}_{2}, die beschreiben, wie die Einheitszelle in der Ebene verschoben werden muss, um das Kachelmuster zu erzeugen. Das heißt, dass die gesamte Ebene gemustert wird, indem die Einheitszelle um m\textbf{b}_{1}+n\textbf{b}_{2} für beliebige ganzzahlige Werte von m and n kopiert wird. Der Betrag des Kreuzprodukts dieser beiden Vektoren wird verwendet, um die Fläche der Einheitszelle zu ermitteln: A_{c} = ||\textbf{b}_{1}\times\textbf{b}_{2}||.

Die rechteckigen, rhomboidischen und hexagonalen Einheitszellen bilden die zweidimensionale Ebene ab. Die Vektoren der Einheitszellen entsprechen zwei Kanten der Zelle, und die Basisvektoren beschreiben, wie die Zellen verschoben werden müssen, um das Muster für die Ebene zu erstellen.
Diese Basisvektoren werden verwendet, um zwei Beugungsvektoren für den reziproken Raum zu definieren: \textbf{d}_{1} = 2\pi(\textbf{b}_{2} \times \textbf{n})/A_{c} und \textbf{d}_{2} = 2\pi(\textbf{n} \times \textbf{b}_{1})/A_{c}, wobei \textbf{n} = (\textbf{b}_{1} \times \textbf{b}_{2})/A_{c} der Normalvektor zur Ebene der Periodizität, der +z-Achse ist. Diese Beugungsvektoren stehen senkrecht zu den Basisvektoren und werden verwendet, um ein Beugungsgitter in der Ebene der Periodizität zu erstellen, indem ganzzahlige Summen gebildet werden:m\textbf{d}_1+n\textbf{d}_2,wobei jeder Punkt des Gitters einem Indexpaar von m und n in den Richtungen \textbf{d}_{1} und \textbf{d}_{2} entspricht. Auf der Transmissionsseite der Einheitszelle befinden sich die Punkte an denselben Stellen, aber die Indizes sind vertauscht und haben entgegengesetzte Vorzeichen.

Die Beugungsvektoren und Gitterpunkte im reziproken Raum.
Wir können diese Beugungspunkte nun auf der Ebene der Periodizität im 3D-Raum visualisieren und eine Halbkugel mit einem Radius gleich den Wellenvektoren im Material oberhalb und unterhalb der Ebene hinzufügen. Diese Halbkugeln informieren uns darüber, welche Beugungsordnungen bei der Reflexion und der Transmission vorhanden sind. Wir zentrieren diese Kugel zunächst auf den Punkt m = 0, n = 0, der das normal einfallende Licht repräsentiert.
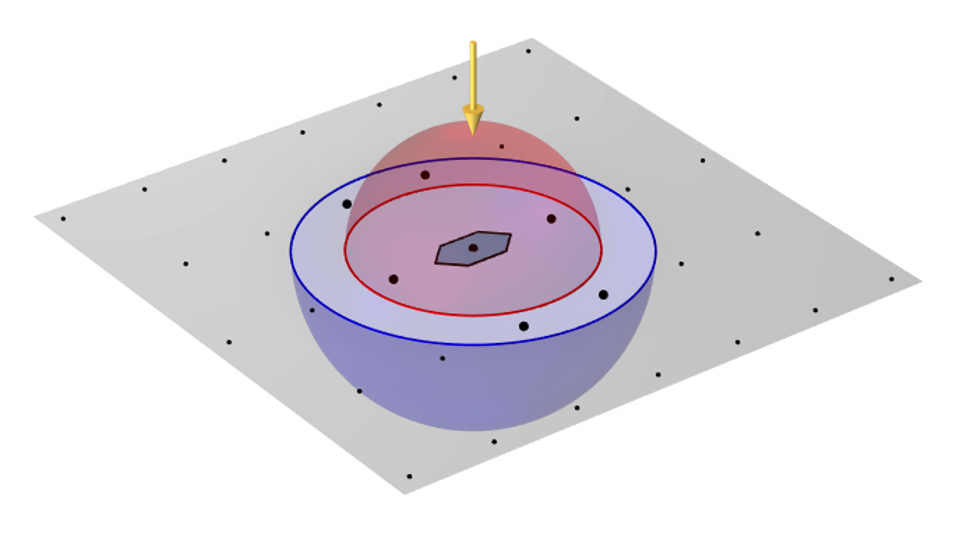
Licht in einer ebenen Welle (gelber Pfeil), das senkrecht auf eine periodische hexagonale Einheitszelle trifft. Die Beugungspunkte sind in der Periodizitätsebene geplottet, und die hervorgehobenen Punkte, die innerhalb der Reflexions- und Transmissionshalbkugeln liegen, zeigen an, welche Beugungsordnungen vorhanden sind.
Als nächstes betrachten wir, was passiert, wenn der Höhen- und der Azimut-Einfallswinkel variiert werden. In Anbetracht dessen, dass wir den Vektor \textbf{a}_{1} auf die +x-Achse ausgerichtet haben, bedeutet eine Vergrößerung des Höhen-Einfallswinkels, dass der Vektor der einfallenden Welle zunächst um die –y-Achse gedreht wird; dann bewirkt eine Vergrößerung des Azimut-Einfallswinkels eine anschließende Drehung um die +z-Achse. Der Höhen-Einfallswinkel ist also 0^{\circ} \le \alpha_{1} < 90^{\circ}, und der Azimut-Einfallswinkel liegt bei 0^{\circ} \le \alpha_{2} < 360^{\circ} , wie unten visualisiert. Der Vektor der einfallenden Welle definiert zusammen mit der Senkrechten auf die Ebene der Periodizität die Einfallsebene. Die Einfallsebene ist definiert als die xz-Ebene für den Fall des senkrechten Einfalls:\alpha_{1} = 0^{\circ}, \alpha_{2} = 0^{\circ}.

Die Höhen- und Azimut-Einfallswinkel stellen eine Reihe von aufeinander folgenden Drehungen des einfallenden Wellenvektors (gelb) dar, zunächst um die –y-Achse und dann um die +z-Achse. Die Einfallsebene ist ebenfalls dargestellt.
Diese Änderungen der Einfallswinkel verändern die Position des Zentrums der Halbkugeln. Der Abstand im reziproken Raum vom Zentrum der Halbkugel zum Punkt m = 0, n = 0 ist k_{r} = \text{sin(}\alpha_{1}\text{)}2π/ \lambda_r, und die Position wird in der Ebene um k_{x} = -k_{r}\text{cos(}\alpha_{2}\text{)} und k_{y} = -k_{r}\text{sin(}\alpha_{2}\text{)} verschoben, wie unten gezeigt. Eine Änderung des Höhenwinkels und des Azimutwinkels führt also oft dazu, dass andere Beugungsordnungen vorhanden ist.
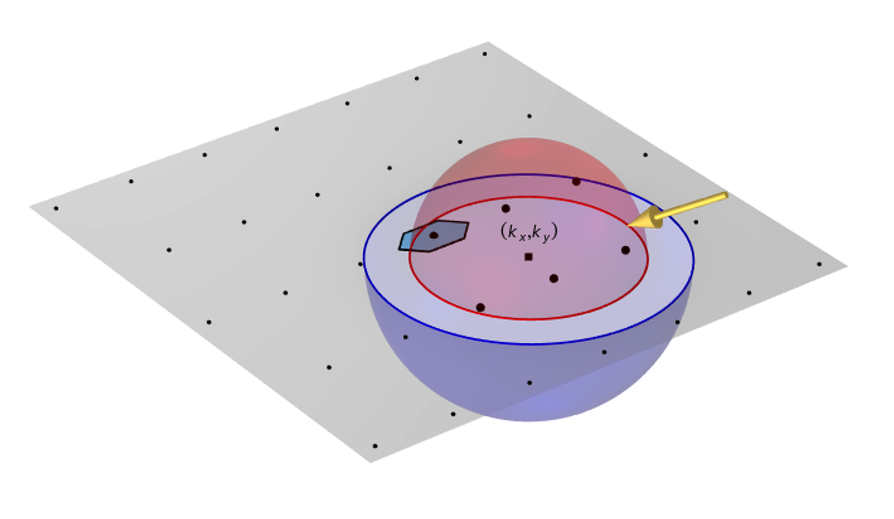
Licht einer ebenen Welle, das in einer Höhe ungleich Null und einem azimutalen Einfallswinkel einfällt, verschiebt den Mittelpunkt der Halbkugeln, so dass andere Beugungsordnungen vorhanden sind.
Diese Halbkugeln geben uns auch die Wellenvektoren jeder Beugungsordnung an. Wenn wir die Punkte der Beugungsordnung auf die Halbkugeln projizieren, erhalten wir einen weitere Reihe von Punkten, und die Wellenvektoren jeder Beugungsordnung entsprechen den Vektoren vom Zentrum der Halbkugel zu diesen projizierten Punkten.
Die Projektion der Beugungspunkte auf die Halbkugeln ergibt den Wellenvektor jeder Beugungsordnung. Diese geometrische Konstruktion veranschaulicht, in welche Richtungen das einfallende Licht (gelb) bei Reflexion (rot) und Transmission (blau) gebeugt wird. Sie können mit diesem 3D-Modell interagieren: Klicken Sie mit der linken Maustaste, um es zu drehen, klicken Sie mit der rechten Maustaste, um es zu schwenken, und vergrößern oder verkleinern Sie es mit dem Mausrad.
Schließlich informieren uns diese Vektoren auch darüber, wie der Polarisationszustand angegeben wird. Für jede Beugungsordnung wird ein Polarisationszustand in Form der in der Ebene und außerhalb der Ebene liegenden Komponenten des Jones-Vektors angegeben. Die Ebene jeder Beugungsordnung ist die Ebene, die durch den Wellenvektor und den Normalenvektor zur Ebene der Periodizität beschrieben wird. Die Komponente außerhalb der Ebene des Jones-Vektors entspricht für alle Beugungsordnungen einer Welle, deren elektrisches Feld parallel zur Ebene der Periodizität verläuft.
Die Richtungen der Beugungsordnungen beschreiben eine Reihe von Ebenen, die verwendet werden, um den Polarisationszustand jeder Beugungsordnung zu definieren. Die Einfallsebene und eine Beugungsordnung sind hervorgehoben. Sie können mit diesem 3D-Modell interagieren: Klicken Sie mit der linken Maustaste, um es zu drehen, klicken Sie mit der rechten Maustaste, um es zu schwenken, und vergrößern oder verkleinern Sie es mit dem Mausrad.
Fazit
Wir haben die geometrische Konstruktion mit Hilfe der Ewald-Kugel abgeschlossen, um die Beugung an planaren periodischen Strukturen zu verstehen, und wir sehen, dass sie uns sagt, welche höheren Beugungsordnungen bei der Reflexion und Transmission auftreten. Sie sagt uns auch, welche Wellenvektoren vorhanden sind und welche Ebenen zur Definition der Ausrichtung der Jones-Vektoren verwendet werden. All diese Informationen erhalten wir automatisch, wenn wir ein numerisches Modell lösen. Diese Art von geometrischer Konstruktion ist also nicht notwendig, aber sie kann hilfreich sein, um unser Verständnis und unsere Intuition zu schärfen.
Weitere Ressourcen
Wenn Sie mit der Modellierung der Beugung höherer Ordnung beginnen möchten, sind die folgenden Beispielmodelle, die mit dem RF Module oder dem Wave Optics Module erstellt werden können, ein guter Ausgangspunkt.
- Modelle aus dem RF Module:
- Modelle aus dem Wave Optics Module:




Kommentare (0)