
Sie wünschen sich einen Leitfaden für die Modellierung von Kabeln? Wir haben eine 8-teilige Tutorial-Reihe für Sie. Die Cable Tutorial Series zeigt, wie man ein industrielles Kabel in der Software COMSOL Multiphysics® und dem Add-On AC/DC Module modelliert, und dient auch als allgemeine Einführung in die Modellierung elektromagnetischer Phänomene. Das numerische Modell basiert auf Standarddesigns von Kabeln und wird durch veröffentlichte Zahlen bestätigt. Hier bekommen Sie einen kleinen Vorgeschmack auf das, was Sie in der Tutorial-Reihe erwartet.
Anmerkung der Redaktion: Dieser Blog-Beitrag wurde ursprünglich am 29. Dezember 2017 veröffentlicht. Er wurde inzwischen aktualisiert, um die aktualisierte Tutorial-Reihe zu berücksichtigen.
Beachten Sie, dass die in diesem Blog-Beitrag besprochenen Modelle nur 2D sind (Teil 1 bis 6 der Reihe). Die 3D-Twist-Modelle (Teil 7 und 8) werden in einem anderen Blog-Beitrag behandelt: Using 3D Models to Investigate Inductive Effects in a Submarine Cable.
Teil 1: Einführung in die Grundlagen der Kabelmodellierung
Der Anfang ist ein sehr guter Startpunkt, wie die meisten sagen würden. In Teil 1 der Tutorial-Reihe lernen Sie das Modell kennen – ein dreiadriges bleiummanteltes XLPE-HVAC-Unterseekabel (vernetztes Polyethylen, Hochspannungs-Wechselstrom) mit einer gedrehten magnetischen Armierung. Außerdem erhalten Sie einen detaillierten Überblick darüber, was Sie in den anderen sieben Teilen der Reihe erfahren werden.

Ein Unterseekabel, ähnlich dem in dieser Reihe dargestellten. Bild von Z22 – Eigenes Werk. Lizensiert unter CC BY-SA 3.0 über Wikimedia Commons.
Diese Einführung ermöglicht es Ihnen, sich mit der benutzerfreundlichen Desktop-Umgebung der Software COMSOL Multiphysics® und mit der numerischen Modellierung im Allgemeinen vertraut zu machen. Sie vermittelt Ihnen die Durchführung grundlegender Aufgaben:
- Zeichnen oder Importieren der 2D-Geometrie
- Hinzufügen der Materialeigenschaften
- Erstellen von Auswahlfiltern
- Vernetzen des Modells
Wenn Sie sich mit diesen Themen bereits auskennen, können Sie die Einführung gerne überspringen.
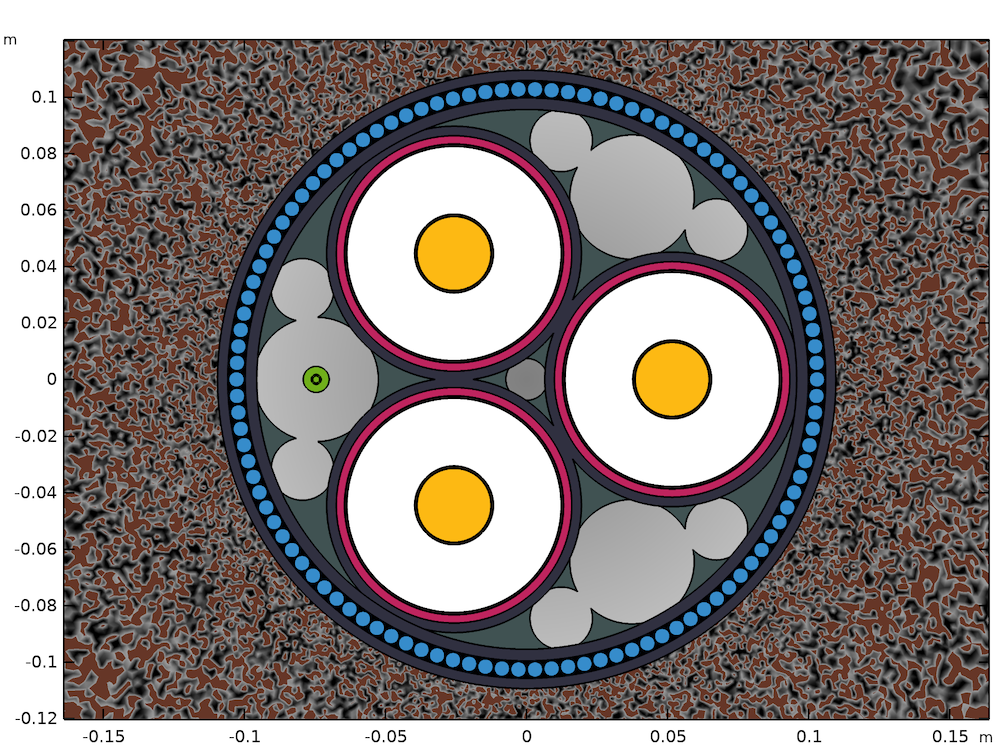
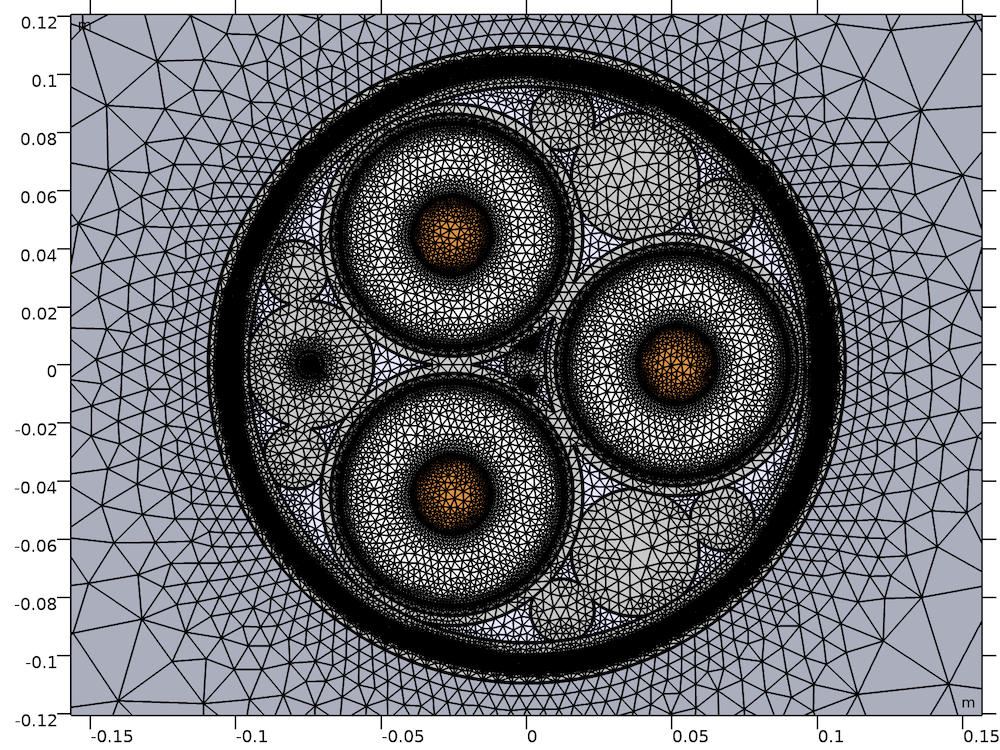
Querschnitt (links) und Netz (rechts) des Modells eines typischen bleiummantelten XLPE-HVAC-Unterseekabels mit drei Adern. Die Geometrie wurde parametrisiert, um schnelle Änderungen zu ermöglichen, so dass jedes Kabel mit der gleichen Grundstruktur leicht untersucht werden kann.
Teil 2: Kapazitive Effekte
Das zweite Tutorial konzentriert sich auf die Modellierung der kapazitiven Eigenschaften des Kabels und bestätigt eine wichtige Annahme: Ein analytischer Ansatz ist für die Analyse der Kapazitäts- und Ladungseffekte ausreichend. Dies wird in der gesamten Reihe von Nutzen sein.
Dieses Tutorial ist für Anfänger gedacht, aber die Ergebnisse stützen auch die anderen Teile der Reihe. Es demonstriert die Bedeutung der Materialeigenschaften und der Kabellänge. Im Querschnitt des Kabelmodells ist es aufgrund der großen Unterschiede in den Materialeigenschaften möglich, das XLPE als perfekten Isolator und die Blei- und Kupfermaterialien als perfekte Leiter zu betrachten. Diese Ergebnisse stimmen mit den analytischen Näherungen überein.
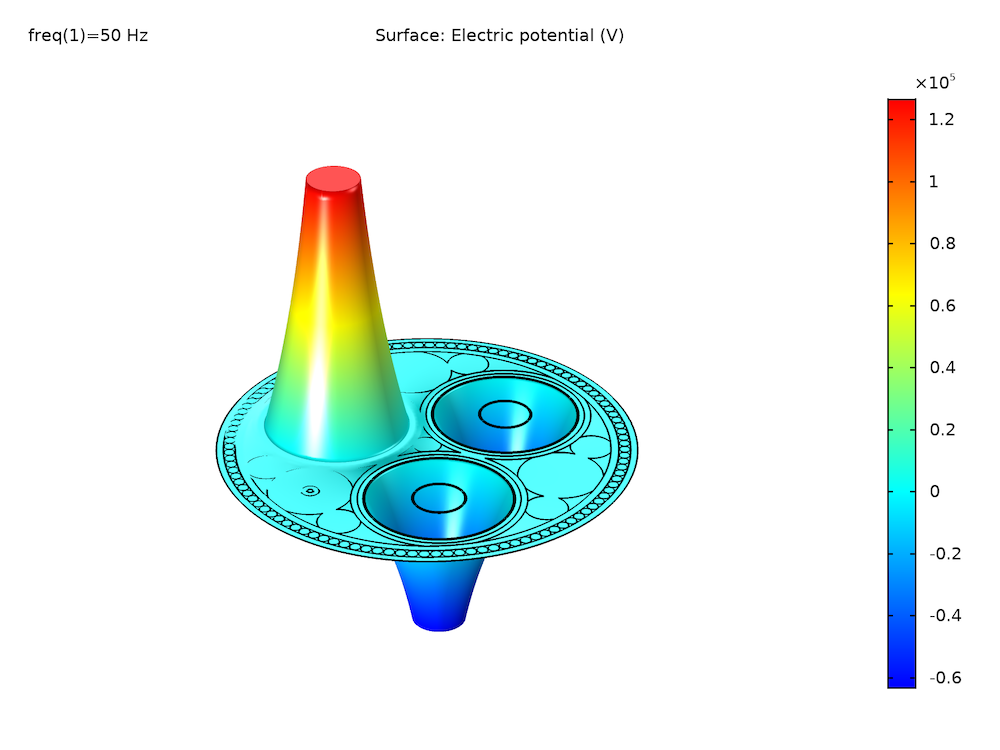
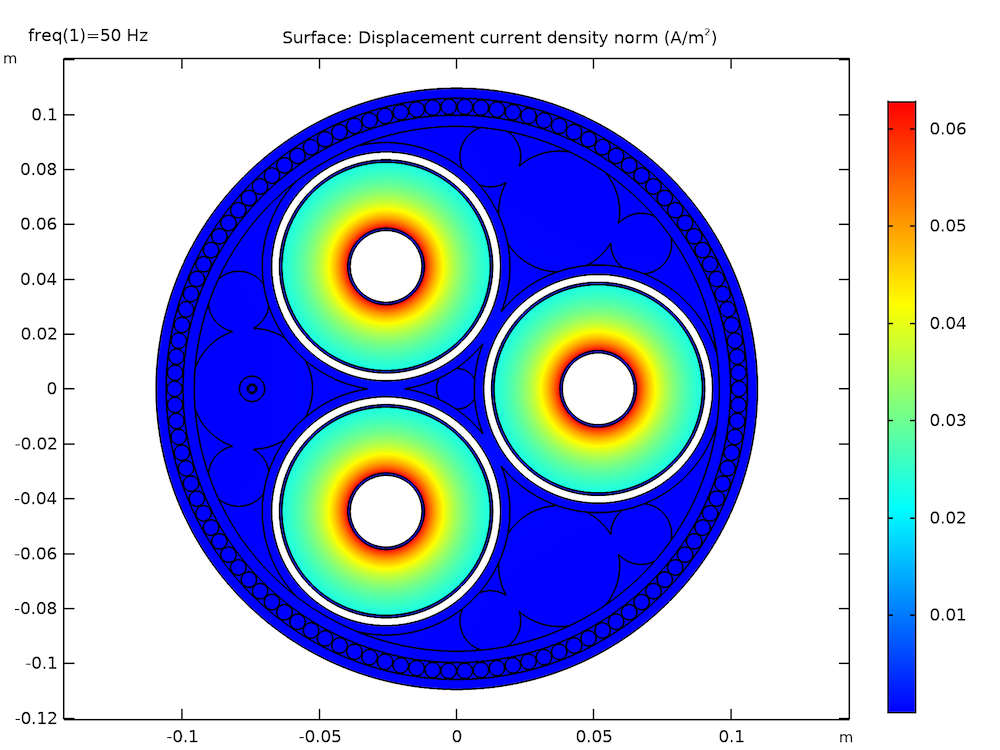
Links: Die Verteilung des elektrischen Potenzials nach 10 km Kabel für Single-Point-Bonding (bei Phase φ = 0). Rechts: Die Norm der Verschiebungsstromdichte der Isolatoren (vor allem des XLPE) in der Ebene.
Hinsichtlich der Kabellänge werden Sie feststellen, dass die analytischen Näherungen für ein 10 km langes Kabel ausreichend sind. Dies gilt selbst unter den ungünstigsten Nennbedingungen, die bei Anwendung von Single-Point-Bonding und phasengleicher Wirkung aller spannungserzeugenden Effekte auftreten.
Teil 3: Kapazitives Bonding
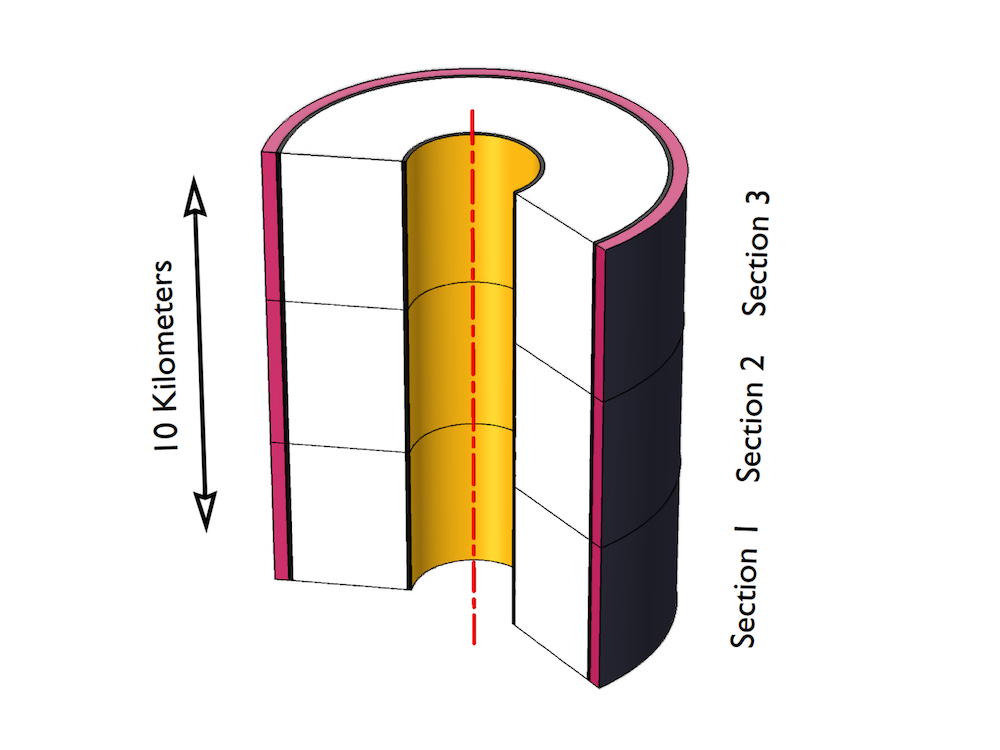
Teil 3 der Reihe baut auf dem vorangegangenen Tutorial auf und zeigt, dass man die kapazitive Kopplung zwischen den Phasen vernachlässigen und eine isolierte Phase betrachten kann. Dadurch wird das Modell auf ein achsensymmetrisches Problem reduziert. Um die vollen 10 Kilometer Kabel zu erfassen, verwenden wir eine skalierte achsensymmetrische 2D-Geometrie im Modell.
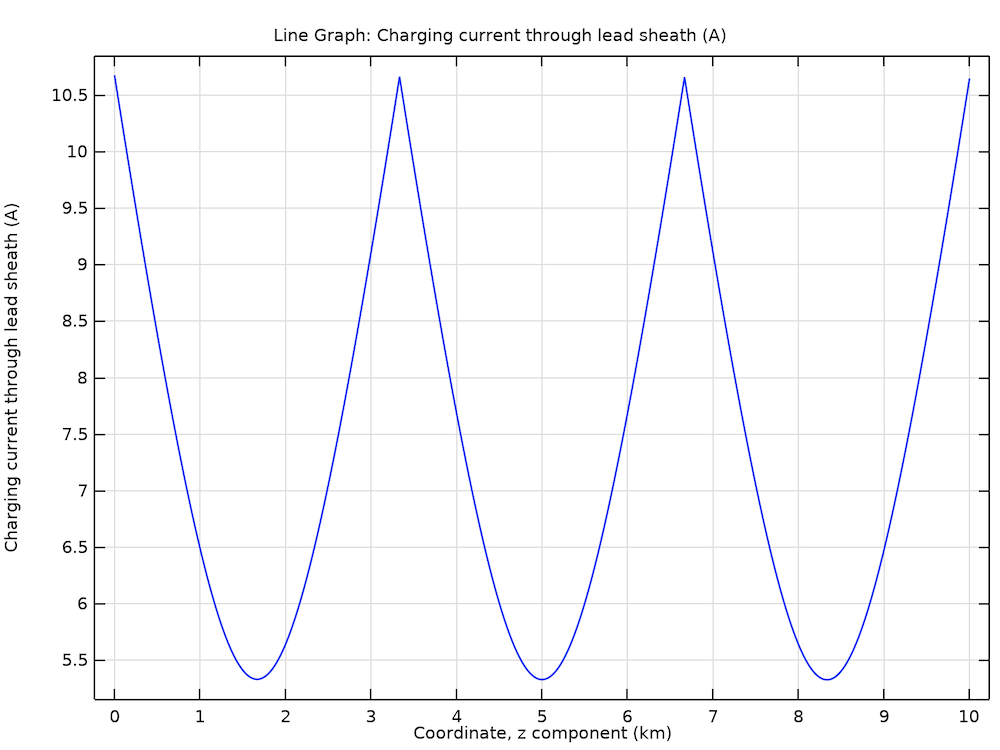
Links: Die achsensymmetrische 2D-Geometrie einer isolierten Phase mit drei getrennten Bindungsabschnitten und einem unterschiedlichen Maßstab für Quer- und Längsrichtung. Rechts: Die Norm des resultierenden Ladestroms, der entlang des Kabels akkumuliert wird (für Cross-Bonding).
Die Ladeströme, die in die Schirmung eindringen, bauen sich entlang des Kabels auf und erreichen am Erdungspunkt bzw. an der Schnittstelle ein Maximum. Das Tutorial Bonding Capacitive analysiert den Stromanstieg für verschiedene Bonding-Typen sowie die entsprechenden Verluste. Das sind die Ergebnisse:
| Bonding-Typ | Gesamter akkumulierter Ladestrom an Erdungspunkt/Schnittstelle | Entsprechende Verluste pro Schirmung |
|---|---|---|
| Single-Point-Bonding | 55 A | 1.5 kW |
| Solid Bonding | 28 A | 0.38 kW |
| Cross-Bonding | 10.7 A | 85 W |
Teil 4: Induktive Effekte
Dieser Teil der Reihe baut auf den beiden vorangegangenen Tutorials auf, die zeigen, dass es eine schwache Kopplung zwischen den induktiven und kapazitiven Teilen des Kabels gibt. Darüber hinaus wird anhand von 3D-Twist-Modellen gezeigt, dass die Feld- und Verlustverteilung in 3D zwar etwas anders ist, die mit 2D- und 2,5D-Modellen berechneten Größen (Widerstand und Induktivität) jedoch ziemlich genau sind. Um dies weiter zu untersuchen, wird im Tutorial Inductive Effects ein 2D/2.5D-Induktionsmodell erstellt, das nur Ströme außerhalb der Ebene berücksichtigt.
Animation der momentanen Norm der magnetischen Flussdichte im Querschnitt des Kabels bei Solid Bonding und einschließlich Armierungsverdrehung.
Animation der Stromdichte, die in der Armierung und den Schirmen des Kabels induziert wird, bei Solid Bonding und einschließlich Armierungsverdrehung.
Das Tutorial konzentriert sich auf Methoden, die es ermöglichen, den Verdrillung des Drahtes sowohl für die magnetische Armierung als auch für die Phasen in 2D anzunähern. Für mehrere Konfigurationen werden die Verluste ausgewertet. Die Konfiguration mit der Armierungsverdrillung wird als „2,5D-Modell“ bezeichnet, da es sich um ein 2D-Modell handelt, das einige 3D-Effekte enthält. Durch die Verdrillung werden die Armierungsströme unterdrückt: Die Armierungsverluste gehen deutlich zurück und die Induktivität steigt.
Darüber hinaus zeigen wir zwei verschiedene Möglichkeiten zur Modellierung der zentralen Leiter. Im ersten Beispiel wird angenommen, dass die zentralen Leiter aus massivem Kupfer bestehen, was zu einem typischen Skin- und Proximity-Effekt führt. Das andere Beispiel zeigt einen Ansatz für einen perfekt verdrillten Litzendraht (einen perfekten Milliken-Leiter), der zu einer homogenisierten Stromdichteverteilung führt. Die Simulationsergebnisse in diesem Tutorial wurden anhand von echten Produktdatenblättern gemäß den offiziellen internationalen Normen bestätigt. Der Vergleich zeigt eine gute Übereinstimmung, insbesondere bei der Induktivität.
Teil 5: Induktives Bonding
Ziel von Teil 5 ist es, die in Teil 3 (und 4) vorgestellten verschiedenen Bonding-Typen weiter zu untersuchen: Single-Point-Bonding, Solid Bonding und Cross-Bonding, welches besonders für terrestrische Kabelanlagen interessant ist. Im Gegensatz zu Teil 3 konzentriert sich dieser Teil auf induktive Effekte.
Sie lernen, wie man durch die Kopplung von drei separaten physikalischen Interfaces Magnetic Fields mit einem Stromkreis drei verschiedene Kabelabschnitte individuell betrachtet. Das daraus resultierende Modell ermöglicht die Untersuchung von unsymmetrischen Kabeln und Kabeln mit ungleichen Abschnittslängen.
Darüber hinaus zeigt das Tutorial die Auswirkungen der Verwendung einer vereinfachten Geometrie. Die Vereinfachung ist ein übergreifendes Thema in dieser Tutorial-Reihe: Es ist oft gerechtfertigt, eine viel einfachere Geometrie zu verwenden, als man denkt. Sie werden sehen, dass es nicht die Menge der Details ist, die ein gutes Modell ausmacht, sondern die Art der Details.
Teil 6: Thermische Effekte
In Teil 6 wird das Kabelmodell um die elektromagnetische Erwärmung und die temperaturabhängige Leitfähigkeit erweitert. Aufbauend auf Teil 4 lernen Sie, wie Sie eine wechselseitige Kopplung zwischen dem elektromagnetischen Feld und dem Wärmetransport einrichten, indem Sie eine frequenz-stationäre Studie durchführen.
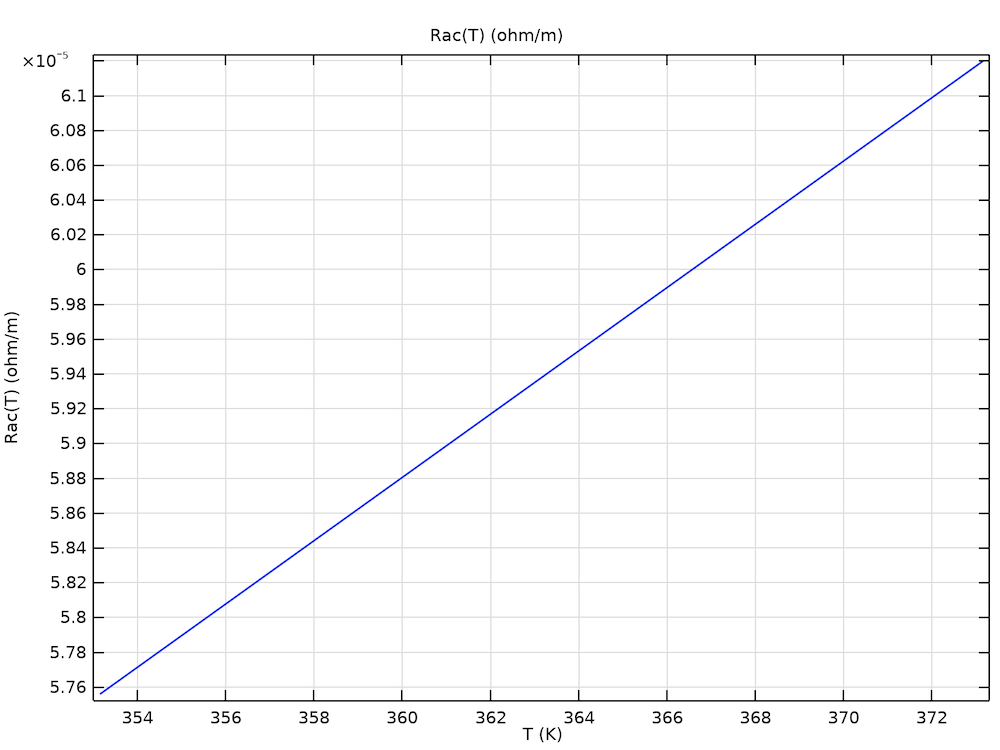
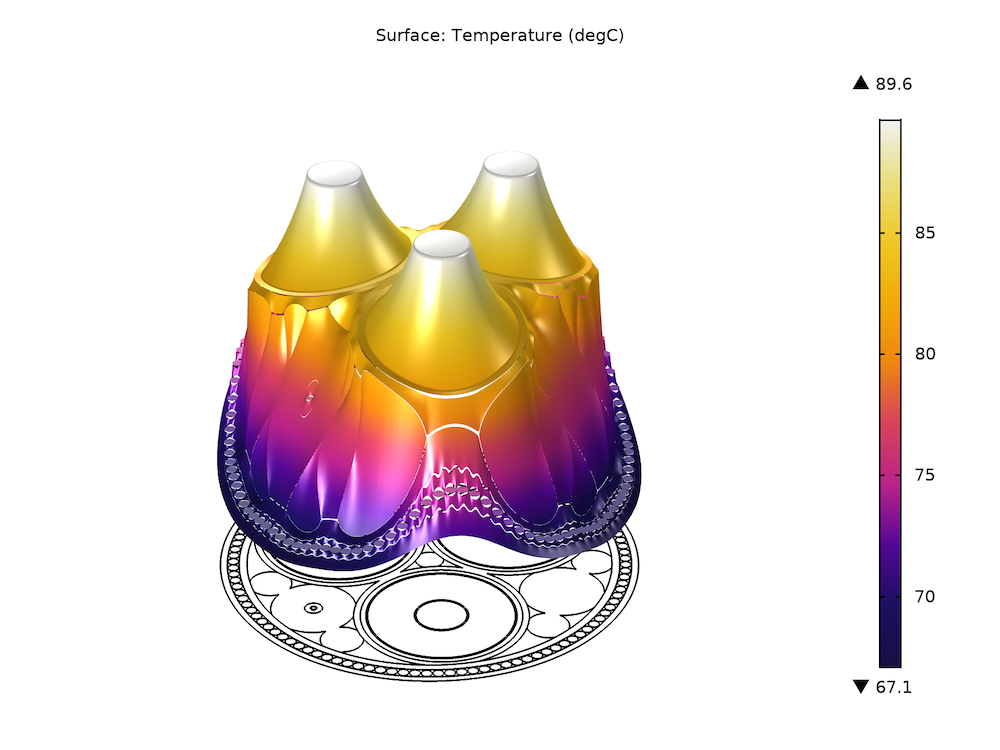
Links: Ein Beispiel für eine voreingestellte Widerstandskurve Rac (T). Rechts: Die resultierende Temperaturverteilung bei Verwendung einer temperaturabhängigen Leitfähigkeit, so dass Rac (T) angepasst wird.
Die Ergebnisse zeigen die Auswirkung der Temperatur auf die Verluste für die Phasen und Schirme des Kabels. Wenn eine elektromagnetische Erwärmung ohne temperaturabhängige Leitfähigkeit hinzugefügt wird, erwärmt sich das Kabel, und doch sind die elektromagnetischen Eigenschaften immer noch identisch mit den in Teil 4 genannten Eigenschaften. Wenn man den linearisierten Widerstand speziell zu den Phasen hinzufügt, erhöhen sich die Phasenverluste, nicht aber die Schirm- und Armierungsverluste. Die Temperatur erreicht ein Maximum. Wird der linearisierte Widerstand auch auf die Schirme und die Armierung angewandt, sinkt die Temperatur und die Verluste nehmen bei den Phasen, den Schirmen und der Armierung ab.
Auch in diesem Fall werden die Materialeigenschaften vorgegeben und das numerische Modell bestimmt den entsprechenden Wechselstromwiderstand. Bei thermischen Kabelmodellen ist es jedoch üblich, wie durch die IEC-Normenreihe 60287 oder durch eine Messung vorgegeben den temperaturabhängigen Wechselstromwiderstand als Eingabe zu verwenden. Im letzten Teil des Tutorials wird gezeigt, wie man eine beliebige temperaturabhängige Widerstandskurve als Eingabe verwenden und das Modell die entsprechenden Phasenmaterialeigenschaften bestimmen lassen kann. Dies ist besonders nützlich, wenn Sie einen anspruchsvollen Milliken-Leiter haben und sich nicht sicher sind, welche effektiven Materialeigenschaften Sie verwenden sollen (d.h. ohne die tatsächlichen Litzen aufzulösen).
Die Ergebnisse dieser 2D-Modelle können mit denen von 3D-Twist-Modellen verglichen werden. Die 3D-Twist-Modelle werden in einem anderen Blog-Beitrag behandelt: Using 3D Models to Investigate Inductive Effects in a Submarine Cable.
Nächste Schritte
Schauen Sie sich die Cable Tutorial Series an, wenn Sie auf der Suche nach Materialien zum Selbststudium der elektromagnetischen Modellierung sind und dabei je nach Interesse einzelne Abschnitte im Detail studieren oder überspringen möchten.
Über diese Schaltfläche können Sie auf die Materialien zugreifen, die eine schrittweise PDF-Anleitung und MPH-Dateien zum Download enthalten:
Sie können außerdem mehr über die Modellierung von Kabelsystemen erfahren, wenn Sie sich dieses archivierte Webinar ansehen.






Kommentare (0)